Arg max

As an example, both unnormalised and normalised sinc functions above have ${\displaystyle \operatorname {argmax} }$ of {0} because both attain their global maximum value of 1 at x = 0.

The unnormalised sinc function (red) has arg min of {−4.49, 4.49}, approximately, because it has 2 global minimum values of approximately −0.217 at x = ±4.49. However, the normalised sinc function (blue) has arg min of {−1.43, 1.43}, approximately, because their global minima occur at x = ±1.43, even though the minimum value is the same.

In mathematics, the arguments of the maxima (abbreviated arg max or argmax) and arguments of the minima (abbreviated arg min or argmin) are the input points at which a function output value is maximized and minimized, respectively. ^{[note 1]} While the arguments are defined over the domain of a function, the output is part of its codomain.

Definition

Given an arbitrary set ${\displaystyle X}$, a totally ordered set ${\displaystyle Y}$, and a function, ${\displaystyle f\colon X\to Y}$, the ${\displaystyle \operatorname {argmax} }$ over some subset ${\displaystyle S}$ of ${\displaystyle X}$ is defined by

${\displaystyle \operatorname {argmax} _{S}f:={\underset {x\in S}{\operatorname {arg\,max} }}\,f(x):=\{x\in S~:~f(s)\leq f(x){\text{ for all }}s\in S\}.}$

If ${\displaystyle S=X}$ or ${\displaystyle S}$ is clear from the context, then ${\displaystyle S}$ is often left out, as in ${\displaystyle {\underset {x}{\operatorname {arg\,max} }}\,f(x):=\{x~:~f(s)\leq f(x){\text{ for all }}s\in X\}.}$ In other words, ${\displaystyle \operatorname {argmax} }$ is the set of points ${\displaystyle x}$ for which ${\displaystyle f(x)}$ attains the function's largest value (if it exists). ${\displaystyle \operatorname {Argmax} }$ may be the empty set, a singleton, or contain multiple elements.

In the fields of convex analysis and variational analysis, a slightly different definition is used in the special case where ${\displaystyle Y=[-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}}$ are the extended real numbers. ^[2] In this case, if ${\displaystyle f}$ is identically equal to ${\displaystyle \infty }$ on ${\displaystyle S}$ then ${\displaystyle \operatorname {argmax} _{S}f:=\varnothing }$ (that is, ${\displaystyle \operatorname {argmax} _{S}\infty$ :=\varnothing }) and otherwise ${\displaystyle \operatorname {argmax} _{S}f}$ is defined as above, where in this case ${\displaystyle \operatorname {argmax} _{S}f}$ can also be written as:

${\displaystyle \operatorname {argmax} _{S}f:=\left\{x\in S~:~f(x)=\sup {}_{S}f\right\}}$

where it is emphasized that this equality involving ${\displaystyle \sup {}_{S}f}$ holds only when ${\displaystyle f}$ is not identically ${\displaystyle \infty }$ on ${\displaystyle S}$. ^[2]

Arg min

The notion of ${\displaystyle \operatorname {argmin} }$ (or ${\displaystyle \operatorname {arg\,min} }$), which stands for argument of the minimum, is defined analogously. For instance,

${\displaystyle {\underset {x\in S}{\operatorname {arg\,min} }}\,f(x):=\{x\in S~:~f(s)\geq f(x){\text{ for all }}s\in S\}}$

are points ${\displaystyle x}$ for which ${\displaystyle f(x)}$ attains its smallest value. It is the complementary operator of ${\displaystyle \operatorname {arg\,max} }$.

In the special case where ${\displaystyle Y=[-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}}$ are the extended real numbers, if ${\displaystyle f}$ is identically equal to ${\displaystyle -\infty }$ on ${\displaystyle S}$ then ${\displaystyle \operatorname {argmin} _{S}f:=\varnothing }$ (that is, ${\displaystyle \operatorname {argmin} _{S}-\infty$ :=\varnothing }) and otherwise ${\displaystyle \operatorname {argmin} _{S}f}$ is defined as above and moreover, in this case (of ${\displaystyle f}$ not identically equal to ${\displaystyle -\infty }$) it also satisfies:

${\displaystyle \operatorname {argmin} _{S}f:=\left\{x\in S~:~f(x)=\inf {}_{S}f\right\}.}$ ^[2]

Examples and properties

For example, if ${\displaystyle f(x)}$ is ${\displaystyle 1-|x|,}$ then ${\displaystyle f}$ attains its maximum value of ${\displaystyle 1}$ only at the point ${\displaystyle x=0.}$ Thus

${\displaystyle {\underset {x}{\operatorname {arg\,max} }}\,(1-|x|)=\{0\}.}$

The ${\displaystyle \operatorname {argmax} }$ operator is different from the ${\displaystyle \max }$ operator. The ${\displaystyle \max }$ operator, when given the same function, returns the maximum value of the function instead of the point or points that cause that function to reach that value; in other words

${\displaystyle \max _{x}f(x)}$ is the element in ${\displaystyle \{f(x)~:~f(s)\leq f(x){\text{ for all }}s\in S\}.}$

Like ${\displaystyle \operatorname {argmax} ,}$ max may be the empty set (in which case the maximum is undefined) or a singleton, but unlike ${\displaystyle \operatorname {argmax} ,}$${\displaystyle \operatorname {max} }$ may not contain multiple elements: ^{[note 2]} for example, if ${\displaystyle f(x)}$ is ${\displaystyle 4x^{2}-x^{4},}$ then ${\displaystyle {\underset {x}{\operatorname {arg\,max} }}\,\left(4x^{2}-x^{4}\right)=\left\{-{\sqrt {2}},{\sqrt {2}}\right\},}$ but ${\displaystyle {\underset {x}{\operatorname {max} }}\,\left(4x^{2}-x^{4}\right)=\{4\}}$ because the function attains the same value at every element of ${\displaystyle \operatorname {argmax} .}$

Equivalently, if ${\displaystyle M}$ is the maximum of ${\displaystyle f,}$ then the ${\displaystyle \operatorname {argmax} }$ is the level set of the maximum:

${\displaystyle {\underset {x}{\operatorname {arg\,max} }}\,f(x)=\{x~:~f(x)=M\}=:f^{-1}(M).}$

We can rearrange to give the simple identity ^{[note 3]}

${\displaystyle f\left({\underset {x}{\operatorname {arg\,max} }}\,f(x)\right)=\max _{x}f(x).}$

If the maximum is reached at a single point then this point is often referred to as the${\displaystyle \operatorname {argmax} ,}$ and ${\displaystyle \operatorname {argmax} }$ is considered a point, not a set of points. So, for example,

${\displaystyle {\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,(x(10-x))=5}$

(rather than the singleton set ${\displaystyle \{5\}}$), since the maximum value of ${\displaystyle x(10-x)}$ is ${\displaystyle 25,}$ which occurs for ${\displaystyle x=5.}$ ^{[note 4]} However, in case the maximum is reached at many points, ${\displaystyle \operatorname {argmax} }$ needs to be considered a set of points.

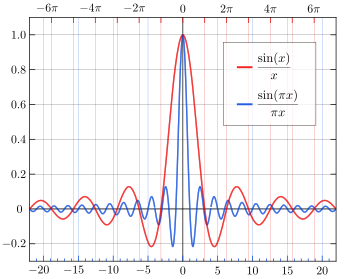
For example

${\displaystyle {\underset {x\in [0,4\pi ]}{\operatorname {arg\,max} }}\,\cos(x)=\{0,2\pi ,4\pi \}}$

because the maximum value of ${\displaystyle \cos x}$ is ${\displaystyle 1,}$ which occurs on this interval for ${\displaystyle x=0,2\pi }$ or ${\displaystyle 4\pi .}$ On the whole real line

${\displaystyle {\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,\cos(x)=\left\{2k\pi ~:~k\in \mathbb {Z} \right\},}$ so an infinite set.

Functions need not in general attain a maximum value, and hence the ${\displaystyle \operatorname {argmax} }$ is sometimes the empty set; for example, ${\displaystyle {\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,x^{3}=\varnothing ,}$ since ${\displaystyle x^{3}}$ is unbounded on the real line. As another example, ${\displaystyle {\underset {x\in \mathbb {R} }{\operatorname {arg\,max} }}\,\arctan(x)=\varnothing ,}$ although ${\displaystyle \arctan }$ is bounded by ${\displaystyle \pm \pi /2.}$ However, by the extreme value theorem, a continuous real-valued function on a closed interval has a maximum, and thus a nonempty ${\displaystyle \operatorname {argmax} .}$

See also

• Argument of a function
• Maxima and minima
• Mode (statistics)
• Mathematical optimization
• Kernel (linear algebra)
• Preimage

Notes

1. For clarity, we refer to the input (x) as points and the output (y) as values; compare critical point and critical value.
2. Due to the anti-symmetry of ${\displaystyle \,\leq ,}$ a function can have at most one maximal value.
3. This is an identity between sets, more particularly, between subsets of ${\displaystyle Y.}$
4. Note that ${\displaystyle x(10-x)=25-(x-5)^{2}\leq 25}$ with equality if and only if ${\displaystyle x-5=0.}$

References

1. "The Unnormalized Sinc Function Archived 2017-02-15 at the Wayback Machine ", University of Sydney
2. Rockafellar & Wets 2009, pp. 1–37.

• Rockafellar, R. Tyrrell; Wets, Roger J.-B. (26 June 2009). Variational Analysis. Grundlehren der mathematischen Wissenschaften. Vol. 317. Berlin New York: Springer Science & Business Media. ISBN   9783642024313. OCLC   883392544.

External links

• arg min and arg max at PlanetMath .