Quadratic programming (QP) is the process of solving certain mathematical optimization problems involving quadratic functions. Specifically, one seeks to optimize a multivariate quadratic function subject to linear constraints on the variables. Quadratic programming is a type of nonlinear programming.

Linear programming (LP), also called linear optimization, is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming.
Branch and bound is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution. It is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm.

In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.
Column generation or delayed column generation is an efficient algorithm for solving large linear programs.
In computer science, an evolution strategy (ES) is an optimization technique based on ideas of evolution. It belongs to the general class of evolutionary computation or artificial evolution methodologies.
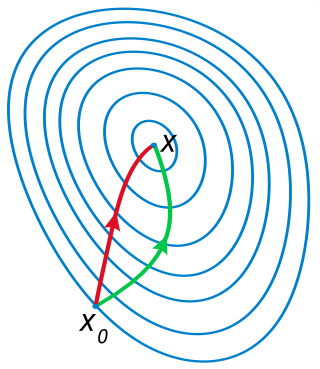
In calculus, Newton's method (also called Newton–Raphson) is an iterative method for finding the roots of a differentiable function F, which are solutions to the equation F (x) = 0. As such, Newton's method can be applied to the derivative f ′ of a twice-differentiable function f to find the roots of the derivative (solutions to f ′(x) = 0), also known as the critical points of f. These solutions may be minima, maxima, or saddle points; see section "Several variables" in Critical point (mathematics) and also section "Geometric interpretation" in this article. This is relevant in optimization, which aims to find (global) minima of the function f.
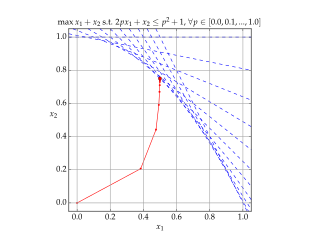
Interior-point methods are a certain class of algorithms that solve linear and nonlinear convex optimization problems.
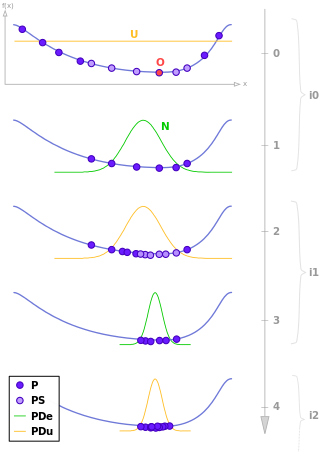
Estimation of distribution algorithms (EDAs), sometimes called probabilistic model-building genetic algorithms (PMBGAs), are stochastic optimization methods that guide the search for the optimum by building and sampling explicit probabilistic models of promising candidate solutions. Optimization is viewed as a series of incremental updates of a probabilistic model, starting with the model encoding an uninformative prior over admissible solutions and ending with the model that generates only the global optima.
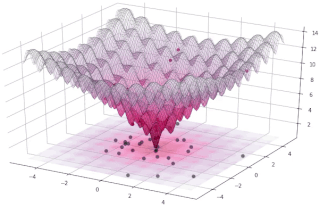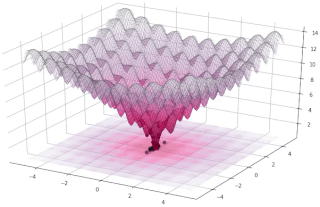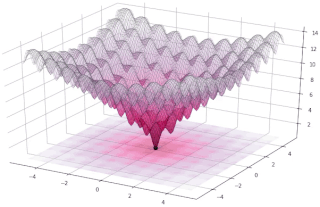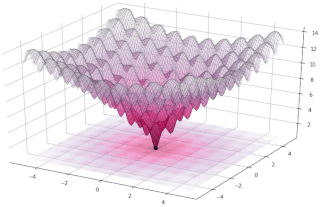
In evolutionary computation, differential evolution (DE) is a method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Such methods are commonly known as metaheuristics as they make few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions. However, metaheuristics such as DE do not guarantee an optimal solution is ever found.
Branch and cut is a method of combinatorial optimization for solving integer linear programs (ILPs), that is, linear programming (LP) problems where some or all the unknowns are restricted to integer values. Branch and cut involves running a branch and bound algorithm and using cutting planes to tighten the linear programming relaxations. Note that if cuts are only used to tighten the initial LP relaxation, the algorithm is called cut and branch.
In mathematical optimization, constrained optimization is the process of optimizing an objective function with respect to some variables in the presence of constraints on those variables. The objective function is either a cost function or energy function, which is to be minimized, or a reward function or utility function, which is to be maximized. Constraints can be either hard constraints, which set conditions for the variables that are required to be satisfied, or soft constraints, which have some variable values that are penalized in the objective function if, and based on the extent that, the conditions on the variables are not satisfied.
Limited-memory BFGS is an optimization algorithm in the family of quasi-Newton methods that approximates the Broyden–Fletcher–Goldfarb–Shanno algorithm (BFGS) using a limited amount of computer memory. It is a popular algorithm for parameter estimation in machine learning. The algorithm's target problem is to minimize over unconstrained values of the real-vector where is a differentiable scalar function.
Covariance matrix adaptation evolution strategy (CMA-ES) is a particular kind of strategy for numerical optimization. Evolution strategies (ES) are stochastic, derivative-free methods for numerical optimization of non-linear or non-convex continuous optimization problems. They belong to the class of evolutionary algorithms and evolutionary computation. An evolutionary algorithm is broadly based on the principle of biological evolution, namely the repeated interplay of variation and selection: in each generation (iteration) new individuals are generated by variation, usually in a stochastic way, of the current parental individuals. Then, some individuals are selected to become the parents in the next generation based on their fitness or objective function value . Like this, over the generation sequence, individuals with better and better -values are generated.

In mathematical optimization, a feasible region, feasible set, search space, or solution space is the set of all possible points of an optimization problem that satisfy the problem's constraints, potentially including inequalities, equalities, and integer constraints. This is the initial set of candidate solutions to the problem, before the set of candidates has been narrowed down.
Multi-objective optimization or Pareto optimization is an area of multiple-criteria decision making that is concerned with mathematical optimization problems involving more than one objective function to be optimized simultaneously. Multi-objective is a type of vector optimization that has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives.
Bootstrapping populations in statistics and mathematics starts with a sample observed from a random variable.
Augmented Lagrangian methods are a certain class of algorithms for solving constrained optimization problems. They have similarities to penalty methods in that they replace a constrained optimization problem by a series of unconstrained problems and add a penalty term to the objective; the difference is that the augmented Lagrangian method adds yet another term, designed to mimic a Lagrange multiplier. The augmented Lagrangian is related to, but not identical with the method of Lagrange multipliers.
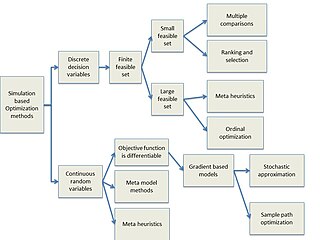
Simulation-based optimization integrates optimization techniques into simulation modeling and analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate. Usually, the underlying simulation model is stochastic, so that the objective function must be estimated using statistical estimation techniques.
Quantum optimization algorithms are quantum algorithms that are used to solve optimization problems. Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. Quantum computing may allow problems which are not practically feasible on classical computers to be solved, or suggest a considerable speed up with respect to the best known classical algorithm.













































