Fitness proportionate selection, also known as roulette wheel selection, is a genetic operator used in genetic algorithms for selecting potentially useful solutions for recombination.
Fitness proportionate selection, also known as roulette wheel selection, is a genetic operator used in genetic algorithms for selecting potentially useful solutions for recombination.
In fitness proportionate selection, as in all selection methods, the fitness function assigns a fitness to possible solutions or chromosomes. This fitness level is used to associate a probability of selection with each individual chromosome. If is the fitness of individual in the population, its probability of being selected is
where is the number of individuals in the population.
This could be imagined similar to a Roulette wheel in a casino. Usually a proportion of the wheel is assigned to each of the possible selections based on their fitness value. This could be achieved by dividing the fitness of a selection by the total fitness of all the selections, thereby normalizing them to 1. Then a random selection is made similar to how the roulette wheel is rotated.
While candidate solutions with a higher fitness will be less likely to be eliminated, there is still a chance that they may be eliminated because their probability of selection is less than 1 (or 100%). Contrast this with a less sophisticated selection algorithm, such as truncation selection, which will eliminate a fixed percentage of the weakest candidates. With fitness proportionate selection there is a chance some weaker solutions may survive the selection process. This is because even though the probability that the weaker solutions will survive is low, it is not zero which means it is still possible they will survive; this is an advantage, because there is a chance that even weak solutions may have some features or characteristics which could prove useful following the recombination process.
The analogy to a roulette wheel can be envisaged by imagining a roulette wheel in which each candidate solution represents a pocket on the wheel; the size of the pockets are proportionate to the probability of selection of the solution.[ citation needed ] Selecting N chromosomes from the population is equivalent to playing N games on the roulette wheel, as each candidate is drawn independently.
The naive implementation is carried out by first generating the cumulative probability distribution (CDF) over the list of individuals using a probability proportional to the fitness of the individual. A uniform random number from the range [0,1) is chosen and the inverse of the CDF for that number gives an individual. This corresponds to the roulette ball falling in the bin of an individual with a probability proportional to its width. The "bin" corresponding to the inverse of the uniform random number can be found most quickly by using a binary search over the elements of the CDF. It takes in the O(log n) time to choose an individual. A faster alternative that generates individuals in O(1) time will be to use the alias method.
In 2011, a very simple algorithm was introduced that is based on "stochastic acceptance". [1] The algorithm randomly selects an individual (say ) and accepts the selection with probability , where is the maximum fitness in the population. Certain analysis indicates that the stochastic acceptance version has a considerably better performance than versions based on linear or binary search, especially in applications where fitness values might change during the run. [2] While the behavior of this algorithm is typically fast, some fitness distributions (such as exponential distributions) may require iterations in the worst case. This algorithm also requires more random numbers than binary search.
For example, if you have a population with fitnesses [1, 2, 3, 4], then the sum is (1 + 2 + 3 + 4 = 10). Therefore, you would want the probabilities or chances to be [1/10, 2/10, 3/10, 4/10] or [0.1, 0.2, 0.3, 0.4]. If you were to visually normalize this between 0.0 and 1.0, it would be grouped like below with [red = 1/10, green = 2/10, blue = 3/10, black = 4/10]:
0.1 ] 0.2 \ 0.3 / 0.4 \ 0.5 | 0.6 / 0.7 \ 0.8 | 0.9 | 1.0 /
Using the above example numbers, this is how to determine the probabilities:
sum_of_fitness = 10 previous_probability = 0.0 [1] = previous_probability + (fitness / sum_of_fitness) = 0.0 + (1 / 10) = 0.1 previous_probability = 0.1 [2] = previous_probability + (fitness / sum_of_fitness) = 0.1 + (2 / 10) = 0.3 previous_probability = 0.3 [3] = previous_probability + (fitness / sum_of_fitness) = 0.3 + (3 / 10) = 0.6 previous_probability = 0.6 [4] = previous_probability + (fitness / sum_of_fitness) = 0.6 + (4 / 10) = 1.0
The last index should always be 1.0 or close to it. Then this is how to randomly select an individual:
random_number # Between 0.0 and 1.0 if random_number < 0.1 select 1else if random_number < 0.3 # 0.3 − 0.1 = 0.2 probability select 2else if random_number < 0.6 # 0.6 − 0.3 = 0.3 probability select 3else if random_number < 1.0 # 1.0 − 0.6 = 0.4 probability select 4end if
Other selection techniques, such as stochastic universal sampling [3] or tournament selection, are often used in practice. This is because they have less stochastic noise, or are fast, easy to implement and have a constant selection pressure. [4]
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event.
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.
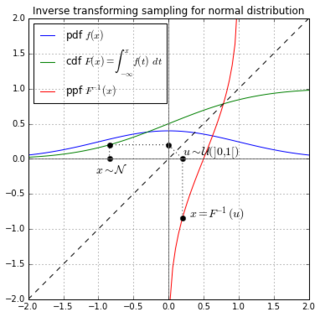
Inverse transform sampling is a basic method for pseudo-random number sampling, i.e., for generating sample numbers at random from any probability distribution given its cumulative distribution function.
Tournament selection is a method of selecting an individual from a population of individuals in a genetic algorithm. Tournament selection involves running several "tournaments" among a few individuals chosen at random from the population. The winner of each tournament is selected for crossover. Selection pressure is then a probabilistic measure of a chromosome's likelihood of participation in the tournament based on the participant selection pool size, is easily adjusted by changing the tournament size. The reason is that if the tournament size is larger, weak individuals have a smaller chance to be selected, because, if a weak individual is selected to be in a tournament, there is a higher probability that a stronger individual is also in that tournament.
Selection is the stage of a genetic algorithm or more general evolutionary algorithm in which individual genomes are chosen from a population for later breeding. Selection mechanisms are also used to choose candidate solutions (individuals) for the next generation. Retaining the best individuals in a generation unchanged in the next generation, is called elitism or elitist selection. It is a successful (slight) variant of the general process of constructing a new population.
A mating pool is a concept used in evolutionary computation, which refers to a family of algorithms used to solve optimization and search problems.
The secretary problem demonstrates a scenario involving optimal stopping theory that is studied extensively in the fields of applied probability, statistics, and decision theory. It is also known as the marriage problem, the sultan's dowry problem, the fussy suitor problem, the googol game, and the best choice problem. Its solution is also known as the 37% rule.
In probability theory and machine learning, the multi-armed bandit problem is a problem in which a decision maker iteratively selects one of multiple fixed choices when the properties of each choice are only partially known at the time of allocation, and may become better understood as time passes. A fundamental aspect of bandit problems is that choosing an arm does not affect the properties of the arm or other arms.
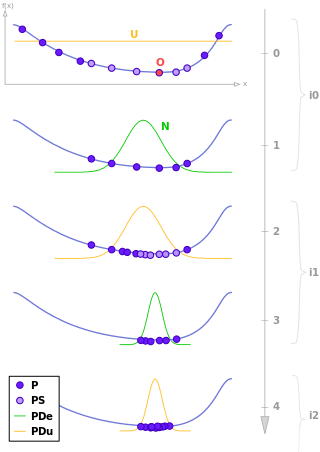
Estimation of distribution algorithms (EDAs), sometimes called probabilistic model-building genetic algorithms (PMBGAs), are stochastic optimization methods that guide the search for the optimum by building and sampling explicit probabilistic models of promising candidate solutions. Optimization is viewed as a series of incremental updates of a probabilistic model, starting with the model encoding an uninformative prior over admissible solutions and ending with the model that generates only the global optima.
In probability theory, the Gillespie algorithm generates a statistically correct trajectory of a stochastic equation system for which the reaction rates are known. It was created by Joseph L. Doob and others, presented by Dan Gillespie in 1976, and popularized in 1977 in a paper where he uses it to simulate chemical or biochemical systems of reactions efficiently and accurately using limited computational power. As computers have become faster, the algorithm has been used to simulate increasingly complex systems. The algorithm is particularly useful for simulating reactions within cells, where the number of reagents is low and keeping track of every single reaction is computationally feasible. Mathematically, it is a variant of a dynamic Monte Carlo method and similar to the kinetic Monte Carlo methods. It is used heavily in computational systems biology.
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.
Covariance matrix adaptation evolution strategy (CMA-ES) is a particular kind of strategy for numerical optimization. Evolution strategies (ES) are stochastic, derivative-free methods for numerical optimization of non-linear or non-convex continuous optimization problems. They belong to the class of evolutionary algorithms and evolutionary computation. An evolutionary algorithm is broadly based on the principle of biological evolution, namely the repeated interplay of variation and selection: in each generation (iteration) new individuals are generated by variation of the current parental individuals, usually in a stochastic way. Then, some individuals are selected to become the parents in the next generation based on their fitness or objective function value . Like this, individuals with better and better -values are generated over the generation sequence.
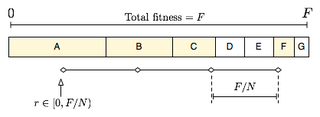
Stochastic universal sampling (SUS) is a technique used in genetic algorithms for selecting potentially useful solutions for recombination. It was introduced by James Baker.
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.
In probability and statistics, the quantile function outputs the value of a random variable such that its probability is less than or equal to an input probability value. Intuitively, the quantile function associates with a range at and below a probability input the likelihood that a random variable is realized in that range for some probability distribution. It is also called the percentile function, percent-point function, inverse cumulative distribution function or inverse distribution function.
In computer science and operations research, the artificial bee colony algorithm (ABC) is an optimization algorithm based on the intelligent foraging behaviour of honey bee swarm, proposed by Derviş Karaboğa in 2005.
Reward-based selection is a technique used in evolutionary algorithms for selecting potentially useful solutions for recombination. The probability of being selected for an individual is proportional to the cumulative reward obtained by the individual. The cumulative reward can be computed as a sum of the individual reward and the reward inherited from parents.
Biogeography-based optimization (BBO) is an evolutionary algorithm (EA) that optimizes a function by stochastically and iteratively improving candidate solutions with regard to a given measure of quality, or fitness function. BBO belongs to the class of metaheuristics since it includes many variations, and since it does not make any assumptions about the problem and can therefore be applied to a wide class of problems.
Mean-field particle methods are a broad class of interacting type Monte Carlo algorithms for simulating from a sequence of probability distributions satisfying a nonlinear evolution equation. These flows of probability measures can always be interpreted as the distributions of the random states of a Markov process whose transition probabilities depends on the distributions of the current random states. A natural way to simulate these sophisticated nonlinear Markov processes is to sample a large number of copies of the process, replacing in the evolution equation the unknown distributions of the random states by the sampled empirical measures. In contrast with traditional Monte Carlo and Markov chain Monte Carlo methods these mean-field particle techniques rely on sequential interacting samples. The terminology mean-field reflects the fact that each of the samples interacts with the empirical measures of the process. When the size of the system tends to infinity, these random empirical measures converge to the deterministic distribution of the random states of the nonlinear Markov chain, so that the statistical interaction between particles vanishes. In other words, starting with a chaotic configuration based on independent copies of initial state of the nonlinear Markov chain model, the chaos propagates at any time horizon as the size the system tends to infinity; that is, finite blocks of particles reduces to independent copies of the nonlinear Markov process. This result is called the propagation of chaos property. The terminology "propagation of chaos" originated with the work of Mark Kac in 1976 on a colliding mean-field kinetic gas model.
The Fly Algorithm is a computational method within the field of evolutionary algorithms, designed for direct exploration of 3D spaces in applications such as computer stereo vision, robotics, and medical imaging. Unlike traditional image-based stereovision, which relies on matching features to construct 3D information, the Fly Algorithm operates by generating a 3D representation directly from random points, termed "flies." Each fly is a coordinate in 3D space, evaluated for its accuracy by comparing its projections in a scene. By iteratively refining the positions of flies based on fitness criteria, the algorithm can construct an optimized spatial representation. The Fly Algorithm has expanded into various fields, including applications in digital art, where it is used to generate complex visual patterns.
