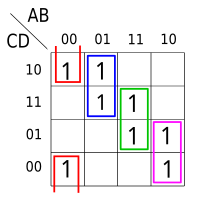In Boolean logic, a formula for a Boolean function f is in Blake canonical form (BCF), [1] also called the complete sum of prime implicants, [2] the complete sum, [3] or the disjunctive prime form, [4] when it is a disjunction of all the prime implicants of f. [1]
The Blake canonical form is a special case of disjunctive normal form.
The Blake canonical form is not necessarily minimal (upper diagram), however all the terms of a minimal sum are contained in the Blake canonical form. [3] On the other hand, the Blake canonical form is a canonical form, that is, it is unique up to reordering, whereas there can be multiple minimal forms (lower diagram). Selecting a minimal sum from a Blake canonical form amounts in general to solving the set cover problem, [5] so is NP-hard. [6] [7]
Archie Blake presented his canonical form at a meeting of the American Mathematical Society in 1932, [8] and in his 1937 dissertation. He called it the "simplified canonical form"; [9] [10] [11] [12] it was named the "Blake canonical form" by Frank Markham Brown and Sergiu Rudeanu in 1986–1990. [13] [1] Together with Platon Poretsky's work [14] it is also referred to as "Blake–Poretsky laws". [15] [ clarification needed ]
Blake discussed three methods for calculating the canonical form: exhaustion of implicants, iterated consensus, and multiplication. The iterated consensus method was rediscovered [1] by Edward W. Samson and Burton E. Mills, [16] Willard Quine, [17] and Kurt Bing. [18] [19] In 2022, Milan Mossé, Harry Sha, and Li-Yang Tan discovered a near-optimal algorithm for computing the Blake canonical form of a formula in conjunctive normal form. [20]
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra.
In boolean logic, a disjunctive normal form (DNF) is a canonical normal form of a logical formula consisting of a disjunction of conjunctions; it can also be described as an OR of ANDs, a sum of products, or — in philosophical logic — a cluster concept. As a normal form, it is useful in automated theorem proving.
The Quine–McCluskey algorithm (QMC), also known as the method of prime implicants, is a method used for minimization of Boolean functions that was developed by Willard V. Quine in 1952 and extended by Edward J. McCluskey in 1956. As a general principle this approach had already been demonstrated by the logician Hugh McColl in 1878, was proved by Archie Blake in 1937, and was rediscovered by Edward W. Samson and Burton E. Mills in 1954 and by Raymond J. Nelson in 1955. Also in 1955, Paul W. Abrahams and John G. Nordahl as well as Albert A. Mullin and Wayne G. Kellner proposed a decimal variant of the method.
Laws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy. LoF describes three distinct logical systems:
In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set. Alternative names are switching function, used especially in older computer science literature, and truth function, used in logic. Boolean functions are the subject of Boolean algebra and switching theory.
In Boolean algebra, any Boolean function can be expressed in the canonical disjunctive normal form (CDNF) or minterm canonical form, and its dual, the canonical conjunctive normal form (CCNF) or maxterm canonical form. Other canonical forms include the complete sum of prime implicants or Blake canonical form, and the algebraic normal form.
In Boolean logic, the term implicant has either a generic or a particular meaning. In the generic use, it refers to the hypothesis of an implication. In the particular use, a product term P is an implicant of a Boolean function F, denoted , if P implies F . For instance, implicants of the function
Platon Sergeevich Poretsky was a noted Russian Imperial astronomer, mathematician, and logician.
In Boolean algebra, Petrick's method is a technique described by Stanley R. Petrick (1931–2006) in 1956 for determining all minimum sum-of-products solutions from a prime implicant chart. Petrick's method is very tedious for large charts, but it is easy to implement on a computer. The method was improved by Insley B. Pyne and Edward Joseph McCluskey in 1962.
Logic is the formal science of using reason and is considered a branch of both philosophy and mathematics and to a lesser extent computer science. Logic investigates and classifies the structure of statements and arguments, both through the study of formal systems of inference and the study of arguments in natural language. The scope of logic can therefore be very large, ranging from core topics such as the study of fallacies and paradoxes, to specialized analyses of reasoning such as probability, correct reasoning, and arguments involving causality. One of the aims of logic is to identify the correct and incorrect inferences. Logicians study the criteria for the evaluation of arguments.
Logic optimization is a process of finding an equivalent representation of the specified logic circuit under one or more specified constraints. This process is a part of a logic synthesis applied in digital electronics and integrated circuit design.
In mathematical logic, algebraic logic is the reasoning obtained by manipulating equations with free variables.
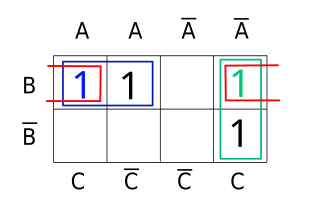
In Boolean algebra, the consensus theorem or rule of consensus is the identity:
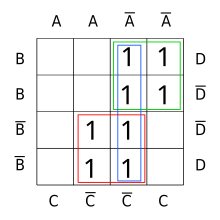
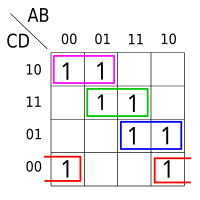
The Karnaugh(/ˈkɑːnɔː/) map is a method of simplifying Boolean algebra expressions. Maurice Karnaugh introduced it in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of Allan Marquand's 1881 logical diagram aka Marquand diagram but now with a focus set on its utility for switching circuits. Veitch charts are also known as Marquand–Veitch diagrams, Svoboda charts -(albeit only rarely)- and even Karnaugh maps as Karnaugh–Veitch maps.
In mathematics and computer science, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions and other mathematical objects. Although computer algebra could be considered a subfield of scientific computing, they are generally considered as distinct fields because scientific computing is usually based on numerical computation with approximate floating point numbers, while symbolic computation emphasizes exact computation with expressions containing variables that have no given value and are manipulated as symbols.
In Boolean algebra, Poretsky's law of forms shows that the single Boolean equation is equivalent to if and only if , where represents exclusive or.
Charles Archibald Blake, name officially changed to Archie Blake was an American mathematician. He is well known for the Blake canonical form, a normal form for expressions in propositional logic. In order to compute the canonical form, he moreover introduced the concept of consensus, which was a precursor of the resolution principle, today a common technique in automated theorem proving.
In theoretical computer science, monotone dualization is a computational problem of constructing the dual of a monotone Boolean function. Equivalent problems can also be formulated as constructing the transversal hypergraph of a given hypergraph, of listing all minimal hitting sets of a family of sets, or of listing all minimal set covers of a family of sets. These problems can be solved in quasi-polynomial time in the combined size of its input and output, but whether they can be solved in polynomial time is an open problem.
Normal forms in logic | ||
|---|---|---|
| Propositional logic |  | |
| Predicate logic | ||
| Other | ||