
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra.
In computational complexity theory, the class NC (for "Nick's Class") is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem with input size n is in NC if there exist constants c and k such that it can be solved in time O((log n)c) using O(nk) parallel processors. Stephen Cook coined the name "Nick's class" after Nick Pippenger, who had done extensive research on circuits with polylogarithmic depth and polynomial size.

In electronics, a multiplexer, also known as a data selector, is a device that selects between several analog or digital input signals and forwards the selected input to a single output line. The selection is directed by a separate set of digital inputs known as select lines. A multiplexer of inputs has select lines, which are used to select which input line to send to the output.
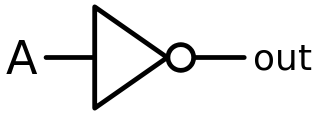
In digital logic, an inverter or NOT gate is a logic gate which implements logical negation. It outputs a bit opposite of the bit that is put into it. The bits are typically implemented as two differing voltage levels.

Exclusive or, exclusive disjunction, exclusive alternation, logical non-equivalence, or logical inequality is a logical operator whose negation is the logical biconditional. With two inputs, XOR is true if and only if the inputs differ. With multiple inputs, XOR is true if and only if the number of true inputs is odd.

The Quine–McCluskey algorithm (QMC), also known as the method of prime implicants, is a method used for minimization of Boolean functions that was developed by Willard V. Quine in 1952 and extended by Edward J. McCluskey in 1956. As a general principle this approach had already been demonstrated by the logician Hugh McColl in 1878, was proved by Archie Blake in 1937, and was rediscovered by Edward W. Samson and Burton E. Mills in 1954 and by Raymond J. Nelson in 1955. Also in 1955, Paul W. Abrahams and John G. Nordahl as well as Albert A. Mullin and Wayne G. Kellner proposed a decimal variant of the method.
An artificial neuron is a mathematical function conceived as a model of biological neurons in a neural network. Artificial neurons are the elementary units of artificial neural networks. The artificial neuron is a function that receives one or more inputs, applies weights to these inputs, and sums them to produce an output.
An adder, or summer, is a digital circuit that performs addition of numbers. In many computers and other kinds of processors, adders are used in the arithmetic logic units (ALUs). They are also used in other parts of the processor, where they are used to calculate addresses, table indices, increment and decrement operators and similar operations.
In computer science, a binary decision diagram (BDD) or branching program is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed representation of sets or relations. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression.
In logic, a truth function is a function that accepts truth values as input and produces a unique truth value as output. In other words: the input and output of a truth function are all truth values; a truth function will always output exactly one truth value, and inputting the same truth value(s) will always output the same truth value. The typical example is in propositional logic, wherein a compound statement is constructed using individual statements connected by logical connectives; if the truth value of the compound statement is entirely determined by the truth value(s) of the constituent statement(s), the compound statement is called a truth function, and any logical connectives used are said to be truth functional.

In quantum information theory, a quantum circuit is a model for quantum computation, similar to classical circuits, in which a computation is a sequence of quantum gates, measurements, initializations of qubits to known values, and possibly other actions. The minimum set of actions that a circuit needs to be able to perform on the qubits to enable quantum computation is known as DiVincenzo's criteria.

In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set. Alternative names are switching function, used especially in older computer science literature, and truth function, used in logic. Boolean functions are the subject of Boolean algebra and switching theory.
Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.

In computational complexity theory and circuit complexity, a Boolean circuit is a mathematical model for combinational digital logic circuits. A formal language can be decided by a family of Boolean circuits, one circuit for each possible input length.
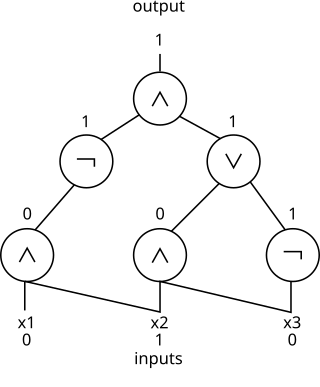
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of the Boolean circuits that compute them. A related notion is the circuit complexity of a recursive language that is decided by a uniform family of circuits .

The Karnaugh(/ˈkɑːnɔː/) map is a method of simplifying Boolean algebra expressions. Maurice Karnaugh introduced it in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of Allan Marquand's 1881 logical diagram aka Marquand diagram but now with a focus set on its utility for switching circuits. Veitch charts are also known as Marquand–Veitch diagrams, Svoboda charts -(albeit only rarely)- and even Karnaugh maps as Karnaugh–Veitch maps.
Zhegalkinpolynomials, also known as algebraic normal form, are a representation of functions in Boolean algebra. Introduced by the Russian mathematician Ivan Ivanovich Zhegalkin in 1927, they are the polynomial ring over the integers modulo 2. The resulting degeneracies of modular arithmetic result in Zhegalkin polynomials being simpler than ordinary polynomials, requiring neither coefficients nor exponents. Coefficients are redundant because 1 is the only nonzero coefficient. Exponents are redundant because in arithmetic mod 2, x2 = x. Hence a polynomial such as 3x2y5z is congruent to, and can therefore be rewritten as, xyz.
In theoretical computer science, a circuit is a model of computation in which input values proceed through a sequence of gates, each of which computes a function. Circuits of this kind provide a generalization of Boolean circuits and a mathematical model for digital logic circuits. Circuits are defined by the gates they contain and the values the gates can produce. For example, the values in a Boolean circuit are boolean values, and the circuit includes conjunction, disjunction, and negation gates. The values in an integer circuit are sets of integers and the gates compute set union, set intersection, and set complement, as well as the arithmetic operations addition and multiplication.
In theoretical computer science, the circuit satisfiability problem is the decision problem of determining whether a given Boolean circuit has an assignment of its inputs that makes the output true. In other words, it asks whether the inputs to a given Boolean circuit can be consistently set to 1 or 0 such that the circuit outputs 1. If that is the case, the circuit is called satisfiable. Otherwise, the circuit is called unsatisfiable. In the figure to the right, the left circuit can be satisfied by setting both inputs to be 1, but the right circuit is unsatisfiable.
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values true and false, usually denoted 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as conjunction (and) denoted as ∧, disjunction (or) denoted as ∨, and the negation (not) denoted as ¬. Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations, in the same way that elementary algebra describes numerical operations.





































