In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.
The development of the nervous system, or neural development, or neurodevelopment, refers to the processes that generate, shape, and reshape the nervous system of animals, from the earliest stages of embryonic development to adulthood. The field of neural development draws on both neuroscience and developmental biology to describe and provide insight into the cellular and molecular mechanisms by which complex nervous systems develop, from nematodes and fruit flies to mammals.

Network theory is the study of graphs as a representation of either symmetric relations or asymmetric relations between discrete objects. In computer science and network science, network theory is a part of graph theory: a network can be defined as a graph in which nodes and/or edges have attributes.
A small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but the neighbors of any given node are likely to be neighbors of each other and most nodes can be reached from every other node by a small number of hops or steps. Specifically, a small-world network is defined to be a network where the typical distance L between two randomly chosen nodes grows proportionally to the logarithm of the number of nodes N in the network, that is:

In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in networks representing real systems. The study of complex networks is a young and active area of scientific research inspired largely by empirical findings of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks.
Axon guidance is a subfield of neural development concerning the process by which neurons send out axons to reach their correct targets. Axons often follow very precise paths in the nervous system, and how they manage to find their way so accurately is an area of ongoing research.

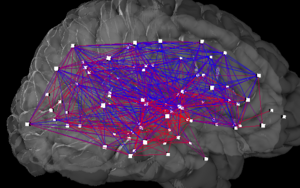
A connectome is a comprehensive map of neural connections in the brain, and may be thought of as its "wiring diagram". More broadly, a connectome would include the mapping of all neural connections within an organism's nervous system.
Connectomics is the production and study of connectomes: comprehensive maps of connections within an organism's nervous system, typically its brain or eye. Because these structures are extremely complex, methods within this field use a high-throughput application of neural imaging and histological techniques in order to increase the speed, efficiency, and resolution of maps of the multitude of neural connections in a nervous system. While the principal focus of such a project is the brain, any neural connections could theoretically be mapped by connectomics, including, for example, neuromuscular junctions. This study is sometimes referred to by its previous name of hodology.
The clique percolation method is a popular approach for analyzing the overlapping community structure of networks. The term network community has no widely accepted unique definition and it is usually defined as a group of nodes that are more densely connected to each other than to other nodes in the network. There are numerous alternative methods for detecting communities in networks, for example, the Girvan–Newman algorithm, hierarchical clustering and modularity maximization.
The friendship paradox is the phenomenon first observed by the sociologist Scott L. Feld in 1991 that most people have fewer friends than their friends have, on average. It can be explained as a form of sampling bias in which people with more friends are more likely to be in one's own friend group. Or, said another way, one is less likely to be friends with someone who has very few friends. In contradiction to this, most people believe that they have more friends than their friends have.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.
The Human Connectome Project (HCP) is a five-year project sponsored by sixteen components of the National Institutes of Health, split between two consortia of research institutions. The project was launched in July 2009 as the first of three Grand Challenges of the NIH's Blueprint for Neuroscience Research. On September 15, 2010, the NIH announced that it would award two grants: $30 million over five years to a consortium led by Washington University in Saint Louis and the University of Minnesota, with strong contributions from Oxford University (FMRIB) and $8.5 million over three years to a consortium led by Harvard University, Massachusetts General Hospital and the University of California Los Angeles.
Connectograms are graphical representations of connectomics, the field of study dedicated to mapping and interpreting all of the white matter fiber connections in the human brain. These circular graphs based on diffusion MRI data utilize graph theory to demonstrate the white matter connections and cortical characteristics for single structures, single subjects, or populations.
A brain atlas is composed of serial sections along different anatomical planes of the healthy or diseased developing or adult animal or human brain where each relevant brain structure is assigned a number of coordinates to define its outline or volume. Brain atlases are contiguous, comprehensive results of visual brain mapping and may include anatomical, genetic or functional features. A functional brain atlas is made up of regions of interest, where these regions are typically defined as spatially contiguous and functionally coherent patches of gray matter.
The bipartite realization problem is a classical decision problem in graph theory, a branch of combinatorics. Given two finite sequences and of natural numbers, the problem asks whether there is labeled simple bipartite graph such that is the degree sequence of this bipartite graph.

Disparity filter is a network reduction algorithm to extract the backbone structure of undirected weighted network. Many real world networks such as citation networks, food web, airport networks display heavy tailed statistical distribution of nodes' weight and strength. Disparity filter can sufficiently reduce the network without destroying the multi-scale nature of the network. The algorithm is developed by M. Angeles Serrano, Marian Boguna and Alessandro Vespignani.
The Giant Virus Finder is a free bioinformatics software for finding giant viruses in metagenomes.

Csaba Pal is a Hungarian biologist at the Biological Research Centre (BRC) in Szeged Hungary. His laboratory is part of the Synthetic and Systems Biology Unit at BRC. His research is at the interface of evolution, antibiotic resistance and genome engineering and has published over 70 scientific publications in these areas.