In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In particle physics, Rutherford scattering is the elastic scattering of charged particles by the Coulomb interaction. It is a physical phenomenon explained by Ernest Rutherford in 1911 that led to the development of the planetary Rutherford model of the atom and eventually the Bohr model. Rutherford scattering was first referred to as Coulomb scattering because it relies only upon the static electric (Coulomb) potential, and the minimum distance between particles is set entirely by this potential. The classical Rutherford scattering process of alpha particles against gold nuclei is an example of "elastic scattering" because neither the alpha particles nor the gold nuclei are internally excited. The Rutherford formula further neglects the recoil kinetic energy of the massive target nucleus.
In optics, Lambert's cosine law says that the radiant intensity or luminous intensity observed from an ideal diffusely reflecting surface or ideal diffuse radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal; I = I0 cos θ. The law is also known as the cosine emission law or Lambert's emission law. It is named after Johann Heinrich Lambert, from his Photometria, published in 1760.

In particle physics, bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

Compton scattering is the quantum theory of high frequency photons scattering following an interaction with a charged particle, usually an electron. Specifically, when the photon hits electrons, it releases loosely bound electrons from the outer valence shells of atoms or molecules.

Pair production is the creation of a subatomic particle and its antiparticle from a neutral boson. Examples include creating an electron and a positron, a muon and an antimuon, or a proton and an antiproton. Pair production often refers specifically to a photon creating an electron–positron pair near a nucleus. As energy must be conserved, for pair production to occur, the incoming energy of the photon must be above a threshold of at least the total rest mass energy of the two particles created. Conservation of energy and momentum are the principal constraints on the process. All other conserved quantum numbers of the produced particles must sum to zero – thus the created particles shall have opposite values of each other. For instance, if one particle has electric charge of +1 the other must have electric charge of −1, or if one particle has strangeness of +1 then another one must have strangeness of −1.
In many areas of science, Bragg's law, Wulff–Bragg's condition, or Laue–Bragg interference are a special case of Laue diffraction, giving the angles for coherent scattering of waves from a large crystal lattice. It describes how the superposition of wave fronts scattered by lattice planes leads to a strict relation between the wavelength and scattering angle. This law was initially formulated for X-rays, but it also applies to all types of matter waves including neutron and electron waves if there are a large number of atoms, as well as visible light with artificial periodic microscale lattices.

Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is the low-energy limit of Compton scattering: the particle's kinetic energy and photon frequency do not change as a result of the scattering. This limit is valid as long as the photon energy is much smaller than the mass energy of the particle: , or equivalently, if the wavelength of the light is much greater than the Compton wavelength of the particle.
In condensed matter physics, scintillation is the physical process where a material, called a scintillator, emits ultraviolet or visible light under excitation from high energy photons or energetic particles. See scintillator and scintillation counter for practical applications.

In particle physics, the Klein–Nishina formula gives the differential cross section of photons scattered from a single free electron, calculated in the lowest order of quantum electrodynamics. It was first derived in 1928 by Oskar Klein and Yoshio Nishina, constituting one of the first successful applications of the Dirac equation. The formula describes both the Thomson scattering of low energy photons and the Compton scattering of high energy photons, showing that the total cross section and expected deflection angle decrease with increasing photon energy.
In quantum physics, the scattering amplitude is the probability amplitude of the outgoing spherical wave relative to the incoming plane wave in a stationary-state scattering process. At large distances from the centrally symmetric scattering center, the plane wave is described by the wavefunction
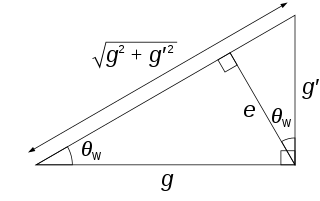
The weak mixing angle or Weinberg angle is a parameter in the Weinberg–Salam theory of the electroweak interaction, part of the Standard Model of particle physics, and is usually denoted as θW. It is the angle by which spontaneous symmetry breaking rotates the original
W0
and
B0
vector boson plane, producing as a result the
Z0
boson, and the photon. Its measured value is slightly below 30°, but also varies, very slightly increasing, depending on how high the relative momentum of the particles involved in the interaction is that the angle is used for.
Elastic recoil detection analysis (ERDA), also referred to as forward recoil scattering, is an ion beam analysis technique in materials science to obtain elemental concentration depth profiles in thin films. This technique is known by several different names. These names are listed below. In the technique of ERDA, an energetic ion beam is directed at a sample to be characterized and there is an elastic nuclear interaction between the ions of beam and the atoms of the target sample. Such interactions are commonly of Coulomb nature. Depending on the kinetics of the ions, cross section area, and the loss of energy of the ions in the matter, ERDA helps determine the quantification of the elemental analysis. It also provides information about the depth profile of the sample.

Electron scattering occurs when electrons are displaced from their original trajectory. This is due to the electrostatic forces within matter interaction or, if an external magnetic field is present, the electron may be deflected by the Lorentz force. This scattering typically happens with solids such as metals, semiconductors and insulators; and is a limiting factor in integrated circuits and transistors.

Møller scattering is the name given to electron-electron scattering in quantum field theory, named after the Danish physicist Christian Møller. The electron interaction that is idealized in Møller scattering forms the theoretical basis of many familiar phenomena such as the repulsion of electrons in the helium atom. While formerly many particle colliders were designed specifically for electron-electron collisions, more recently electron-positron colliders have become more common. Nevertheless, Møller scattering remains a paradigmatic process within the theory of particle interactions.

In quantum electrodynamics, Bhabha scattering is the electron-positron scattering process:
Rutherford backscattering spectrometry (RBS) is an analytical technique used in materials science. Sometimes referred to as high-energy ion scattering (HEIS) spectrometry, RBS is used to determine the structure and composition of materials by measuring the backscattering of a beam of high energy ions (typically protons or alpha particles) impinging on a sample.

Modeling photon propagation with Monte Carlo methods is a flexible yet rigorous approach to simulate photon transport. In the method, local rules of photon transport are expressed as probability distributions which describe the step size of photon movement between sites of photon-matter interaction and the angles of deflection in a photon's trajectory when a scattering event occurs. This is equivalent to modeling photon transport analytically by the radiative transfer equation (RTE), which describes the motion of photons using a differential equation. However, closed-form solutions of the RTE are often not possible; for some geometries, the diffusion approximation can be used to simplify the RTE, although this, in turn, introduces many inaccuracies, especially near sources and boundaries. In contrast, Monte Carlo simulations can be made arbitrarily accurate by increasing the number of photons traced. For example, see the movie, where a Monte Carlo simulation of a pencil beam incident on a semi-infinite medium models both the initial ballistic photon flow and the later diffuse propagation.
The Kapitza–Dirac effect is a quantum mechanical effect consisting of the diffraction of matter by a standing wave of light. The effect was first predicted as the diffraction of electrons from a standing wave of light by Paul Dirac and Pyotr Kapitsa in 1933. The effect relies on the wave–particle duality of matter as stated by the de Broglie hypothesis in 1924.
Surface-extended X-ray absorption fine structure (SEXAFS) is the surface-sensitive equivalent of the EXAFS technique. This technique involves the illumination of the sample by high-intensity X-ray beams from a synchrotron and monitoring their photoabsorption by detecting in the intensity of Auger electrons as a function of the incident photon energy. Surface sensitivity is achieved by the interpretation of data depending on the intensity of the Auger electrons instead of looking at the relative absorption of the X-rays as in the parent method, EXAFS.















