Del in cylindrical and spherical coordinates

This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.

Notes

• This article uses the standard notation ISO 80000-2, which supersedes ISO 31-11, for spherical coordinates (other sources may reverse the definitions of θ and φ):
  • The polar angle is denoted by ${\displaystyle \theta \in [0,\pi ]}$: it is the angle between the z-axis and the radial vector connecting the origin to the point in question.
  • The azimuthal angle is denoted by ${\displaystyle \varphi \in [0,2\pi ]}$: it is the angle between the x-axis and the projection of the radial vector onto the xy-plane.
• The function atan2(y, x) can be used instead of the mathematical function arctan(y/x) owing to its domain and image. The classical arctan function has an image of (−π/2, +π/2), whereas atan2 is defined to have an image of (−π, π].

Coordinate conversions

Conversion between Cartesian, cylindrical, and spherical coordinates ^[1]

		From
		Cartesian	Cylindrical	Spherical
To	Cartesian	${\displaystyle {\begin{aligned}x&=x\\y&=y\\z&=z\\\end{aligned}}}$	${\displaystyle {\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}x&=r\sin \theta \cos \varphi \\y&=r\sin \theta \sin \varphi \\z&=r\cos \theta \\\end{aligned}}}$
	Cylindrical	${\displaystyle {\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &=\arctan \left({\frac {y}{x}}\right)\\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}\rho &=\rho \\\varphi &=\varphi \\z&=z\\\end{aligned}}}$	${\displaystyle {\begin{aligned}\rho &=r\sin \theta \\\varphi &=\varphi \\z&=r\cos \theta \end{aligned}}}$
	Spherical	${\displaystyle {\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)\\\varphi &=\arctan \left({\frac {y}{x}}\right)\end{aligned}}}$	${\displaystyle {\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}}\\\theta &=\arctan {\left({\frac {\rho }{z}}\right)}\\\varphi &=\varphi \end{aligned}}}$	${\displaystyle {\begin{aligned}r&=r\\\theta &=\theta \\\varphi &=\varphi \end{aligned}}}$

CAUTION: the operation ${\displaystyle \arctan \left({\frac {A}{B}}\right)}$ must be interpreted as the two-argument inverse tangent, atan2.

Unit vector conversions

Conversion between unit vectors in Cartesian, cylindrical, and spherical coordinate systems in terms of destination coordinates ^[1]

	Cartesian	Cylindrical	Spherical
Cartesian	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\hat {\mathbf {x} }}\\{\hat {\mathbf {y} }}&={\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\cos \varphi {\hat {\boldsymbol {\rho }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \varphi {\hat {\boldsymbol {\rho }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\sin \theta \cos \varphi {\hat {\mathbf {r} }}+\cos \theta \cos \varphi {\hat {\boldsymbol {\theta }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \theta \sin \varphi {\hat {\mathbf {r} }}+\cos \theta \sin \varphi {\hat {\boldsymbol {\theta }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}}$
Cylindrical	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\hat {\boldsymbol {\rho }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\sin \theta {\hat {\mathbf {r} }}+\cos \theta {\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}}$
Spherical	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}+z{\hat {\mathbf {z} }}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {\left(x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}\right)z-\left(x^{2}+y^{2}\right){\hat {\mathbf {z} }}}{{\sqrt {x^{2}+y^{2}+z^{2}}}{\sqrt {x^{2}+y^{2}}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {\rho {\hat {\boldsymbol {\rho }}}+z{\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {z{\hat {\boldsymbol {\rho }}}-\rho {\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\hat {\mathbf {r} }}\\{\hat {\boldsymbol {\theta }}}&={\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\\end{aligned}}}$

Conversion between unit vectors in Cartesian, cylindrical, and spherical coordinate systems in terms of source coordinates

	Cartesian	Cylindrical	Spherical
Cartesian	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\hat {\mathbf {x} }}\\{\hat {\mathbf {y} }}&={\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x{\hat {\boldsymbol {\rho }}}-y{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {y} }}&={\frac {y{\hat {\boldsymbol {\rho }}}+x{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)-y{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {y} }}&={\frac {y\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)+x{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-{\sqrt {x^{2}+y^{2}}}{\hat {\boldsymbol {\theta }}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\end{aligned}}}$
Cylindrical	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\hat {\boldsymbol {\rho }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {\rho {\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-\rho {\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\end{aligned}}}$
Spherical	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta {\hat {\boldsymbol {\rho }}}+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta {\hat {\boldsymbol {\rho }}}-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\hat {\mathbf {r} }}\\{\hat {\boldsymbol {\theta }}}&={\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\\end{aligned}}}$

Del formula

Table with the del operator in cartesian, cylindrical and spherical coordinates

Operation	Cartesian coordinates (x, y, z)	Cylindrical coordinates (ρ, φ, z)	Spherical coordinates (r, θ, φ), where θ is the polar angle and φ is the azimuthal angle α
Vector field A	${\displaystyle A_{x}{\hat {\mathbf {x} }}+A_{y}{\hat {\mathbf {y} }}+A_{z}{\hat {\mathbf {z} }}}$	${\displaystyle A_{\rho }{\hat {\boldsymbol {\rho }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}+A_{z}{\hat {\mathbf {z} }}}$	${\displaystyle A_{r}{\hat {\mathbf {r} }}+A_{\theta }{\hat {\boldsymbol {\theta }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}}$
Gradient ∇f [1]	${\displaystyle {\partial f \over \partial x}{\hat {\mathbf {x} }}+{\partial f \over \partial y}{\hat {\mathbf {y} }}+{\partial f \over \partial z}{\hat {\mathbf {z} }}}$	${\displaystyle {\partial f \over \partial \rho }{\hat {\boldsymbol {\rho }}}+{1 \over \rho }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}+{\partial f \over \partial z}{\hat {\mathbf {z} }}}$	${\displaystyle {\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}}$
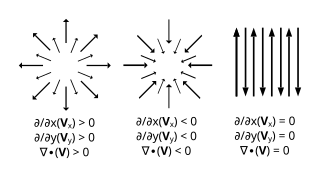
Divergence ∇ ⋅ A [1]	${\displaystyle {\partial A_{x} \over \partial x}+{\partial A_{y} \over \partial y}+{\partial A_{z} \over \partial z}}$	${\displaystyle {1 \over \rho }{\partial \left(\rho A_{\rho }\right) \over \partial \rho }+{1 \over \rho }{\partial A_{\varphi } \over \partial \varphi }+{\partial A_{z} \over \partial z}}$	${\displaystyle {1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\varphi } \over \partial \varphi }}$
Curl ∇ × A [1]	${\displaystyle {\begin{aligned}\left({\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right)&{\hat {\boldsymbol {\rho }}}\\+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+{\frac {1}{\rho }}\left({\frac {\partial \left(\rho A_{\varphi }\right)}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \varphi }}\right)&{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{\frac {1}{r\sin \theta }}\left({\frac {\partial }{\partial \theta }}\left(A_{\varphi }\sin \theta \right)-{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\{}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {\partial }{\partial r}}\left(rA_{\varphi }\right)\right)&{\hat {\boldsymbol {\theta }}}\\{}+{\frac {1}{r}}\left({\frac {\partial }{\partial r}}\left(rA_{\theta }\right)-{\frac {\partial A_{r}}{\partial \theta }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Laplace operator ∇2f ≡ ∆f [1]	${\displaystyle {\partial ^{2}f \over \partial x^{2}}+{\partial ^{2}f \over \partial y^{2}}+{\partial ^{2}f \over \partial z^{2}}}$	${\displaystyle {1 \over \rho }{\partial \over \partial \rho }\left(\rho {\partial f \over \partial \rho }\right)+{1 \over \rho ^{2}}{\partial ^{2}f \over \partial \varphi ^{2}}+{\partial ^{2}f \over \partial z^{2}}}$	${\displaystyle {1 \over r^{2}}{\partial \over \partial r}\!\left(r^{2}{\partial f \over \partial r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\partial \over \partial \theta }\!\left(\sin \theta {\partial f \over \partial \theta }\right)\!+\!{1 \over r^{2}\!\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}}$
Vector gradient ∇A β	${\displaystyle {\begin{aligned}{}&{\frac {\partial A_{x}}{\partial x}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{x}}{\partial y}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{x}}{\partial z}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{y}}{\partial x}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{y}}{\partial y}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{y}}{\partial z}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{z}}{\partial x}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{z}}{\partial y}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{z}}{\partial z}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{}&{\frac {\partial A_{\rho }}{\partial \rho }}{\hat {\boldsymbol {\rho }}}\otimes {\hat {\boldsymbol {\rho }}}+\left({\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \varphi }}-{\frac {A_{\varphi }}{\rho }}\right){\hat {\boldsymbol {\rho }}}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{\rho }}{\partial z}}{\hat {\boldsymbol {\rho }}}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{\varphi }}{\partial \rho }}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\rho }}}+\left({\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {A_{\rho }}{\rho }}\right){\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{\varphi }}{\partial z}}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{z}}{\partial \rho }}{\hat {\mathbf {z} }}\otimes {\hat {\boldsymbol {\rho }}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}{\hat {\mathbf {z} }}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{z}}{\partial z}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}{}&{\frac {\partial A_{r}}{\partial r}}{\hat {\mathbf {r} }}\otimes {\hat {\mathbf {r} }}+\left({\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {A_{\theta }}{r}}\right){\hat {\mathbf {r} }}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {A_{\varphi }}{r}}\right){\hat {\mathbf {r} }}\otimes {\hat {\boldsymbol {\varphi }}}\\{}+&{\frac {\partial A_{\theta }}{\partial r}}{\hat {\boldsymbol {\theta }}}\otimes {\hat {\mathbf {r} }}+\left({\frac {1}{r}}{\frac {\partial A_{\theta }}{\partial \theta }}+{\frac {A_{r}}{r}}\right){\hat {\boldsymbol {\theta }}}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}-\cot \theta {\frac {A_{\varphi }}{r}}\right){\hat {\boldsymbol {\theta }}}\otimes {\hat {\boldsymbol {\varphi }}}\\{}+&{\frac {\partial A_{\varphi }}{\partial r}}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial A_{\varphi }}{\partial \theta }}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+\cot \theta {\frac {A_{\theta }}{r}}+{\frac {A_{r}}{r}}\right){\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Vector Laplacian ∇2A ≡ ∆A [2]	${\displaystyle \nabla ^{2}A_{x}{\hat {\mathbf {x} }}+\nabla ^{2}A_{y}{\hat {\mathbf {y} }}+\nabla ^{2}A_{z}{\hat {\mathbf {z} }}}$	${\displaystyle {\begin{aligned}{\mathopen {}}\left(\nabla ^{2}A_{\rho }-{\frac {A_{\rho }}{\rho ^{2}}}-{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\rho }}}\\+{\mathopen {}}\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{\rho ^{2}}}+{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\varphi }}}\\{}+\nabla ^{2}A_{z}&{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\left(\nabla ^{2}A_{r}-{\frac {2A_{r}}{r^{2}}}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial \left(A_{\theta }\sin \theta \right)}{\partial \theta }}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\+\left(\nabla ^{2}A_{\theta }-{\frac {A_{\theta }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}+{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Directional derivative (A ⋅ ∇)B [3]	${\displaystyle \mathbf {A} \cdot \nabla B_{x}{\hat {\mathbf {x} }}+\mathbf {A} \cdot \nabla B_{y}{\hat {\mathbf {y} }}+\mathbf {A} \cdot \nabla B_{z}{\hat {\mathbf {z} }}}$	${\displaystyle {\begin{aligned}\left(A_{\rho }{\frac {\partial B_{\rho }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\rho }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\rho }}{\partial z}}-{\frac {A_{\varphi }B_{\varphi }}{\rho }}\right)&{\hat {\boldsymbol {\rho }}}\\+\left(A_{\rho }{\frac {\partial B_{\varphi }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\varphi }}{\partial z}}+{\frac {A_{\varphi }B_{\rho }}{\rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+\left(A_{\rho }{\frac {\partial B_{z}}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{z}}{\partial \varphi }}+A_{z}{\frac {\partial B_{z}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\left(A_{r}{\frac {\partial B_{r}}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{r}}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{r}}{\partial \varphi }}-{\frac {A_{\theta }B_{\theta }+A_{\varphi }B_{\varphi }}{r}}\right)&{\hat {\mathbf {r} }}\\+\left(A_{r}{\frac {\partial B_{\theta }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\theta }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\theta }}{\partial \varphi }}+{\frac {A_{\theta }B_{r}}{r}}-{\frac {A_{\varphi }B_{\varphi }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(A_{r}{\frac {\partial B_{\varphi }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\varphi }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+{\frac {A_{\varphi }B_{r}}{r}}+{\frac {A_{\varphi }B_{\theta }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Tensor divergence ∇ ⋅ T γ	${\displaystyle {\begin{aligned}\left({\frac {\partial T_{xx}}{\partial x}}+{\frac {\partial T_{yx}}{\partial y}}+{\frac {\partial T_{zx}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial T_{xy}}{\partial x}}+{\frac {\partial T_{yy}}{\partial y}}+{\frac {\partial T_{zy}}{\partial z}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial T_{xz}}{\partial x}}+{\frac {\partial T_{yz}}{\partial y}}+{\frac {\partial T_{zz}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi r}}{\partial \varphi }}-{\frac {1}{r}}(T_{\theta \theta }+T_{\varphi \varphi })\right]&{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta }+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \theta }}{\partial \varphi }}+{\frac {T_{\theta r}}{r}}-{\frac {\cot \theta }{r}}T_{\varphi \varphi }\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta })\right]&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
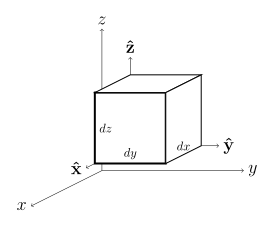
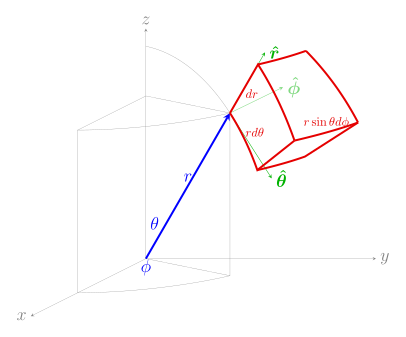
Differential displacement dℓ [1]	${\displaystyle dx\,{\hat {\mathbf {x} }}+dy\,{\hat {\mathbf {y} }}+dz\,{\hat {\mathbf {z} }}}$	${\displaystyle d\rho \,{\hat {\boldsymbol {\rho }}}+\rho \,d\varphi \,{\hat {\boldsymbol {\varphi }}}+dz\,{\hat {\mathbf {z} }}}$	${\displaystyle dr\,{\hat {\mathbf {r} }}+r\,d\theta \,{\hat {\boldsymbol {\theta }}}+r\,\sin \theta \,d\varphi \,{\hat {\boldsymbol {\varphi }}}}$
Differential normal area dS	${\displaystyle {\begin{aligned}dy\,dz&\,{\hat {\mathbf {x} }}\\{}+dx\,dz&\,{\hat {\mathbf {y} }}\\{}+dx\,dy&\,{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\rho \,d\varphi \,dz&\,{\hat {\boldsymbol {\rho }}}\\{}+d\rho \,dz&\,{\hat {\boldsymbol {\varphi }}}\\{}+\rho \,d\rho \,d\varphi &\,{\hat {\mathbf {z} }}\end{aligned}}}$	${\displaystyle {\begin{aligned}r^{2}\sin \theta \,d\theta \,d\varphi &\,{\hat {\mathbf {r} }}\\{}+r\sin \theta \,dr\,d\varphi &\,{\hat {\boldsymbol {\theta }}}\\{}+r\,dr\,d\theta &\,{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
Differential volume dV [1]	${\displaystyle dx\,dy\,dz}$	${\displaystyle \rho \,d\rho \,d\varphi \,dz}$	${\displaystyle r^{2}\sin \theta \,dr\,d\theta \,d\varphi }$

^α This page uses ${\displaystyle \theta }$ for the polar angle and ${\displaystyle \varphi }$ for the azimuthal angle, which is common notation in physics. The source that is used for these formulae uses ${\displaystyle \theta }$ for the azimuthal angle and ${\displaystyle \varphi }$ for the polar angle, which is common mathematical notation. In order to get the mathematics formulae, switch ${\displaystyle \theta }$ and ${\displaystyle \varphi }$ in the formulae shown in the table above.

^β Defined in Cartesian coordinates as ${\displaystyle \partial _{i}\mathbf {A} \otimes \mathbf {e} _{i}}$. An alternative definition is ${\displaystyle \mathbf {e} _{i}\otimes \partial _{i}\mathbf {A} }$.

^γ Defined in Cartesian coordinates as ${\displaystyle \mathbf {e} _{i}\cdot \partial _{i}\mathbf {T} }$. An alternative definition is ${\displaystyle \partial _{i}\mathbf {T} \cdot \mathbf {e} _{i}}$.

Calculation rules

1. ${\displaystyle \operatorname {div} \,\operatorname {grad} f\equiv \nabla \cdot \nabla f\equiv \nabla ^{2}f}$
2. ${\displaystyle \operatorname {curl} \,\operatorname {grad} f\equiv \nabla \times \nabla f=\mathbf {0} }$
3. ${\displaystyle \operatorname {div} \,\operatorname {curl} \mathbf {A} \equiv \nabla \cdot (\nabla \times \mathbf {A} )=0}$
4. ${\displaystyle \operatorname {curl} \,\operatorname {curl} \mathbf {A} \equiv \nabla \times (\nabla \times \mathbf {A} )=\nabla (\nabla \cdot \mathbf {A} )-\nabla ^{2}\mathbf {A} }$ (Lagrange's formula for del)
5. ${\displaystyle \nabla ^{2}(fg)=f\nabla ^{2}g+2\nabla f\cdot \nabla g+g\nabla ^{2}f}$
6. ${\displaystyle \nabla ^{2}\left(\mathbf {P} \cdot \mathbf {Q} \right)=\mathbf {Q} \cdot \nabla ^{2}\mathbf {P} -\mathbf {P} \cdot \nabla ^{2}\mathbf {Q} +2\nabla \cdot \left[\left(\mathbf {P} \cdot \nabla \right)\mathbf {Q} +\mathbf {P} \times \nabla \times \mathbf {Q} \right]\quad }$ (From ^[4] )

Cartesian derivation

$${\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} =\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}&={\frac {A_{x}(x+dx)\,dy\,dz-A_{x}(x)\,dy\,dz+A_{y}(y+dy)\,dx\,dz-A_{y}(y)\,dx\,dz+A_{z}(z+dz)\,dx\,dy-A_{z}(z)\,dx\,dy}{dx\,dy\,dz}}\\&={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{x}=\lim _{S^{\perp \mathbf {\hat {x}} }\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{z}(y+dy)\,dz-A_{z}(y)\,dz+A_{y}(z)\,dy-A_{y}(z+dz)\,dy}{dy\,dz}}\\&={\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\end{aligned}}}$$

The expressions for ${\displaystyle (\operatorname {curl} \mathbf {A} )_{y}}$ and ${\displaystyle (\operatorname {curl} \mathbf {A} )_{z}}$ are found in the same way.

Cylindrical derivation

$${\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{\rho }(\rho +d\rho )(\rho +d\rho )\,d\phi \,dz-A_{\rho }(\rho )\rho \,d\phi \,dz+A_{\phi }(\phi +d\phi )\,d\rho \,dz-A_{\phi }(\phi )\,d\rho \,dz+A_{z}(z+dz)\,d\rho \,(\rho +d\rho /2)\,d\phi -A_{z}(z)\,d\rho (\rho +d\rho /2)\,d\phi }{\rho \,d\phi \,d\rho \,dz}}\\&={\frac {1}{\rho }}{\frac {\partial (\rho A_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial A_{\phi }}{\partial \phi }}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\rho }&=\lim _{S^{\perp {\hat {\boldsymbol {\rho }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\[1ex]&={\frac {A_{\phi }(z)\left(\rho +d\rho \right)\,d\phi -A_{\phi }(z+dz)\left(\rho +d\rho \right)\,d\phi +A_{z}(\phi +d\phi )\,dz-A_{z}(\phi )\,dz}{\left(\rho +d\rho \right)\,d\phi \,dz}}\\[1ex]&=-{\frac {\partial A_{\phi }}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }&=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\&={\frac {A_{z}(\rho )\,dz-A_{z}(\rho +d\rho )\,dz+A_{\rho }(z+dz)\,d\rho -A_{\rho }(z)\,d\rho }{d\rho \,dz}}\\&=-{\frac {\partial A_{z}}{\partial \rho }}+{\frac {\partial A_{\rho }}{\partial z}}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\hat {\boldsymbol {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\[1ex]&={\frac {A_{\rho }(\phi )\,d\rho -A_{\rho }(\phi +d\phi )\,d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )\,d\phi -A_{\phi }(\rho )\rho \,d\phi }{\rho \,d\rho \,d\phi }}\\[1ex]&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{\rho }{\hat {\boldsymbol {\rho }}}+(\operatorname {curl} \mathbf {A} )_{\phi }{\hat {\boldsymbol {\phi }}}+(\operatorname {curl} \mathbf {A} )_{z}{\hat {\boldsymbol {z}}}\\[1ex]&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}-{\frac {\partial A_{\phi }}{\partial z}}\right){\hat {\boldsymbol {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\hat {\boldsymbol {\phi }}}+{\frac {1}{\rho }}\left({\frac {\partial (\rho A_{\phi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \phi }}\right){\hat {\boldsymbol {z}}}\end{aligned}}}$$

Spherical derivation

$${\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{r}(r+dr)(r+dr)\,d\theta \,(r+dr)\sin \theta \,d\phi -A_{r}(r)r\,d\theta \,r\sin \theta \,d\phi +A_{\theta }(\theta +d\theta )\sin(\theta +d\theta )r\,dr\,d\phi -A_{\theta }(\theta )\sin(\theta )r\,dr\,d\phi +A_{\phi }(\phi +d\phi )r\,dr\,d\theta -A_{\phi }(\phi )r\,dr\,d\theta }{dr\,r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r^{2}}}{\frac {\partial (r^{2}A_{r})}{\partial r}}+{\frac {1}{r\sin \theta }}{\frac {\partial (A_{\theta }\sin \theta )}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{r}=\lim _{S^{\perp {\boldsymbol {\hat {r}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\theta }(\phi )r\,d\theta +A_{\phi }(\theta +d\theta )r\sin(\theta +d\theta )\,d\phi -A_{\theta }(\phi +d\phi )r\,d\theta -A_{\phi }(\theta )r\sin(\theta )\,d\phi }{r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \phi }}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\theta }=\lim _{S^{\perp {\boldsymbol {\hat {\theta }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\phi }(r)r\sin \theta \,d\phi +A_{r}(\phi +d\phi )\,dr-A_{\phi }(r+dr)(r+dr)\sin \theta \,d\phi -A_{r}(\phi )\,dr}{dr\,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {1}{r}}{\frac {\partial (rA_{\phi })}{\partial r}}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{r}(\theta )\,dr+A_{\theta }(r+dr)(r+dr)\,d\theta -A_{r}(\theta +d\theta )\,dr-A_{\theta }(r)r\,d\theta }{r\,dr\,d\theta }}\\&={\frac {1}{r}}{\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}\\[1ex]&={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \phi }}\right){\hat {\boldsymbol {r}}}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial (rA_{\phi })}{\partial r}}\right){\hat {\boldsymbol {\theta }}}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\hat {\boldsymbol {\phi }}}\end{aligned}}}$$

Unit vector conversion formula

The unit vector of a coordinate parameter u is defined in such a way that a small positive change in u causes the position vector ${\displaystyle \mathbf {r} }$ to change in ${\displaystyle \mathbf {u} }$ direction.

Therefore,

$${\displaystyle {\frac {\partial {\mathbf {r} }}{\partial u}}={\frac {\partial {s}}{\partial u}}\mathbf {u} }$$

where s is the arc length parameter.

For two sets of coordinate systems ${\displaystyle u_{i}}$ and ${\displaystyle v_{j}}$, according to chain rule,

$${\displaystyle d\mathbf {r} =\sum _{i}{\frac {\partial \mathbf {r} }{\partial u_{i}}}\,du_{i}=\sum _{i}{\frac {\partial s}{\partial u_{i}}}{\hat {\mathbf {u} }}_{i}du_{i}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\hat {\mathbf {v} }}_{j}\,dv_{j}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\hat {\mathbf {v} }}_{j}\sum _{i}{\frac {\partial v_{j}}{\partial u_{i}}}\,du_{i}=\sum _{i}\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\frac {\partial v_{j}}{\partial u_{i}}}{\hat {\mathbf {v} }}_{j}\,du_{i}.}$$

Now, we isolate the ${\displaystyle i}$^th component. For ${\displaystyle i{\neq }k}$, let ${\displaystyle \mathrm {d} u_{k}=0}$. Then divide on both sides by ${\displaystyle \mathrm {d} u_{i}}$ to get:

$${\displaystyle {\frac {\partial s}{\partial u_{i}}}{\hat {\mathbf {u} }}_{i}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\frac {\partial v_{j}}{\partial u_{i}}}{\hat {\mathbf {v} }}_{j}.}$$

See also

• Del
• Orthogonal coordinates
• Curvilinear coordinates
• Vector fields in cylindrical and spherical coordinates

References

1. Griffiths, David J. (2012). Introduction to Electrodynamics. Pearson. ISBN   978-0-321-85656-2.
2. Arfken, George; Weber, Hans; Harris, Frank (2012). Mathematical Methods for Physicists (Seventh ed.). Academic Press. p. 192. ISBN   9789381269558.
3. Weisstein, Eric W. "Convective Operator". Mathworld. Retrieved 23 March 2011.
4. Fernández-Guasti, M. (2012). "Green's Second Identity for Vector Fields". ISRN Mathematical Physics. 2012. Hindawi Limited: 1–7. doi: 10.5402/2012/973968 . ISSN   2090-4681.

External links

• Maxima Computer Algebra system scripts to generate some of these operators in cylindrical and spherical coordinates.