
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including aerodynamics and hydrodynamics. Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation.
Laminar flow is the property of fluid particles in fluid dynamics to follow smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mixing, and adjacent layers slide past one another smoothly. There are no cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluids. In laminar flow, the motion of the particles of the fluid is very orderly with particles close to a solid surface moving in straight lines parallel to that surface. Laminar flow is a flow regime characterized by high momentum diffusion and low momentum convection.
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as:
In thermal fluid dynamics, the Nusselt number is the ratio of total heat transfer to conductive heat transfer at a boundary in a fluid. Total heat transfer combines conduction and convection. Convection includes both advection and diffusion (conduction). The conductive component is measured under the same conditions as the convective but for a hypothetically motionless fluid. It is a dimensionless number, closely related to the fluid's Rayleigh number.
In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.
In fluid dynamics, the Darcy–Weisbach equation is an empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation is named after Henry Darcy and Julius Weisbach. Currently, there is no formula more accurate or universally applicable than the Darcy-Weisbach supplemented by the Moody diagram or Colebrook equation.

In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition. The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.
In thermodynamics, the heat transfer coefficient or film coefficient, or film effectiveness, is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat. It is used in calculating the heat transfer, typically by convection or phase transition between a fluid and a solid. The heat transfer coefficient has SI units in watts per square meter per kelvin (W/m²K).

In fluid mechanics, plug flow is a simple model of the velocity profile of a fluid flowing in a pipe. In plug flow, the velocity of the fluid is assumed to be constant across any cross-section of the pipe perpendicular to the axis of the pipe. The plug flow model assumes there is no boundary layer adjacent to the inner wall of the pipe.
In fluid dynamics, the Schmidt number of a fluid is a dimensionless number defined as the ratio of momentum diffusivity and mass diffusivity, and it is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975).
The Stanton number, St, is a dimensionless number that measures the ratio of heat transferred into a fluid to the thermal capacity of fluid. The Stanton number is named after Thomas Stanton (engineer) (1865–1931). It is used to characterize heat transfer in forced convection flows.

In fluid dynamics, the law of the wall states that the average velocity of a turbulent flow at a certain point is proportional to the logarithm of the distance from that point to the "wall", or the boundary of the fluid region. This law of the wall was first published in 1930 by Hungarian-American mathematician, aerospace engineer, and physicist Theodore von Kármán. It is only technically applicable to parts of the flow that are close to the wall, though it is a good approximation for the entire velocity profile of natural streams.
This page describes some of the parameters used to characterize the thickness and shape of boundary layers formed by fluid flowing along a solid surface. The defining characteristic of boundary layer flow is that at the solid walls, the fluid's velocity is reduced to zero. The boundary layer refers to the thin transition layer between the wall and the bulk fluid flow. The boundary layer concept was originally developed by Ludwig Prandtl and is broadly classified into two types, bounded and unbounded. The differentiating property between bounded and unbounded boundary layers is whether the boundary layer is being substantially influenced by more than one wall. Each of the main types has a laminar, transitional, and turbulent sub-type. The two types of boundary layers use similar methods to describe the thickness and shape of the transition region with a couple of exceptions detailed in the Unbounded Boundary Layer Section. The characterizations detailed below consider steady flow but is easily extended to unsteady flow.
The Reynolds Analogy is popularly known to relate turbulent momentum and heat transfer. That is because in a turbulent flow the transport of momentum and the transport of heat largely depends on the same turbulent eddies: the velocity and the temperature profiles have the same shape.
The turbulent Prandtl number (Prt) is a non-dimensional term defined as the ratio between the momentum eddy diffusivity and the heat transfer eddy diffusivity. It is useful for solving the heat transfer problem of turbulent boundary layer flows. The simplest model for Prt is the Reynolds analogy, which yields a turbulent Prandtl number of 1. From experimental data, Prt has an average value of 0.85, but ranges from 0.7 to 0.9 depending on the Prandtl number of the fluid in question.
In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Hagen in 1839 and then by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845.

In fluid dynamics, the Reynolds number is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers, flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow. These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation.
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.
Skin friction drag is a type of aerodynamic or hydrodynamic drag, which is resistant force exerted on an object moving in a fluid. Skin friction drag is caused by the viscosity of fluids and is developed from laminar drag to turbulent drag as a fluid moves on the surface of an object. Skin friction drag is generally expressed in terms of the Reynolds number, which is the ratio between inertial force and viscous force.
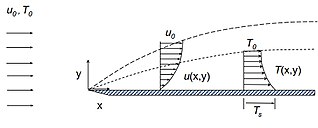
This page describes some parameters used to characterize the properties of the thermal boundary layer formed by a heated fluid moving along a heated wall. In many ways, the thermal boundary layer description parallels the velocity (momentum) boundary layer description first conceptualized by Ludwig Prandtl. Consider a fluid of uniform temperature and velocity impinging onto a stationary plate uniformly heated to a temperature . Assume the flow and the plate are semi-infinite in the positive/negative direction perpendicular to the plane. As the fluid flows along the wall, the fluid at the wall surface satisfies a no-slip boundary condition and has zero velocity, but as you move away from the wall, the velocity of the flow asymptotically approaches the free stream velocity . The temperature at the solid wall is and gradually changes to as one moves toward the free stream of the fluid. It is impossible to define a sharp point at which the thermal boundary layer fluid or the velocity boundary layer fluid becomes the free stream, yet these layers have a well-defined characteristic thickness given by and . The parameters below provide a useful definition of this characteristic, measurable thickness for the thermal boundary layer. Also included in this boundary layer description are some parameters useful in describing the shape of the thermal boundary layer.














































