In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three numbers, : the radial distance of the radial liner connecting the point to the fixed point of origin ; the polar angle θ of the radial line r; and the azimuthal angle φ of the radial line r.

In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force. The symbol for torque is typically , the lowercase Greek letter tau. When being referred to as moment of force, it is commonly denoted by M. Just as a linear force is a push or a pull applied to a body, a torque can be thought of as a twist applied to an object with respect to a chosen point; for example, driving a screw uses torque, which is applied by the screwdriver rotating around its axis. A force of three newtons applied two metres from the fulcrum, for example, exerts the same torque as a force of one newton applied six metres from the fulcrum.

In physics and mathematics, in the area of dynamical systems, a double pendulum also known as a chaotic pendulum is a pendulum with another pendulum attached to its end, forming a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions. The motion of a double pendulum is governed by a set of coupled ordinary differential equations and is chaotic.
Kinematics is a subfield of physics and mathematics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of both applied and pure mathematics since it can be studied without considering the mass of a body or the forces acting upon it. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.

An inverted pendulum is a pendulum that has its center of mass above its pivot point. It is unstable and falls over without additional help. It can be suspended stably in this inverted position by using a control system to monitor the angle of the pole and move the pivot point horizontally back under the center of mass when it starts to fall over, keeping it balanced. The inverted pendulum is a classic problem in dynamics and control theory and is used as a benchmark for testing control strategies. It is often implemented with the pivot point mounted on a cart that can move horizontally under control of an electronic servo system as shown in the photo; this is called a cart and pole apparatus. Most applications limit the pendulum to 1 degree of freedom by affixing the pole to an axis of rotation. Whereas a normal pendulum is stable when hanging downward, an inverted pendulum is inherently unstable, and must be actively balanced in order to remain upright; this can be done either by applying a torque at the pivot point, by moving the pivot point horizontally as part of a feedback system, changing the rate of rotation of a mass mounted on the pendulum on an axis parallel to the pivot axis and thereby generating a net torque on the pendulum, or by oscillating the pivot point vertically. A simple demonstration of moving the pivot point in a feedback system is achieved by balancing an upturned broomstick on the end of one's finger.
In analytical mechanics, generalized coordinates are a set of parameters used to represent the state of a system in a configuration space. These parameters must uniquely define the configuration of the system relative to a reference state. The generalized velocities are the time derivatives of the generalized coordinates of the system. The adjective "generalized" distinguishes these parameters from the traditional use of the term "coordinate" to refer to Cartesian coordinates.
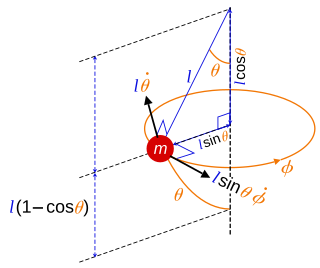
In physics, a spherical pendulum is a higher dimensional analogue of the pendulum. It consists of a mass m moving without friction on the surface of a sphere. The only forces acting on the mass are the reaction from the sphere and gravity.
In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M. The analogous solution for a charged, rotating body is given by the Kerr–Newman metric.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the linear rotor requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water, ammonia, or methane.
The Schwarzschild solution describes spacetime under the influence of a massive, non-rotating, spherically symmetric object. It is considered by some to be one of the simplest and most useful solutions to the Einstein field equations.

An osculating circle is a circle that best approximates the curvature of a curve at a specific point. It is tangent to the curve at that point and has the same curvature as the curve at that point. The osculating circle provides a way to understand the local behavior of a curve and is commonly used in differential geometry and calculus.

In classical mechanics, Routh's procedure or Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by Edward John Routh. Correspondingly, the Routhian is the function which replaces both the Lagrangian and Hamiltonian functions. Routhian mechanics is equivalent to Lagrangian mechanics and Hamiltonian mechanics, and introduces no new physics. It offers an alternative way to solve mechanical problems.

A pendulum is a body suspended from a fixed support such that it freely swings back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back towards the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.

The swinging Atwood's machine (SAM) is a mechanism that resembles a simple Atwood's machine except that one of the masses is allowed to swing in a two-dimensional plane, producing a dynamical system that is chaotic for some system parameters and initial conditions.

Rotational diffusion is the rotational movement which acts upon any object such as particles, molecules, atoms when present in a fluid, by random changes in their orientations. Whilst the directions and intensities of these changes are statistically random, they do not arise randomly and are instead the result of interactions between particles. One example occurs in colloids, where relatively large insoluble particles are suspended in a greater amount of fluid. The changes in orientation occur from collisions between the particle and the many molecules forming the fluid surrounding the particle, which each transfer kinetic energy to the particle, and as such can be considered random due to the varied speeds and amounts of fluid molecules incident on each individual particle at any given time.

In physics and mathematics, in the area of dynamical systems, an elastic pendulum is a physical system where a piece of mass is connected to a spring so that the resulting motion contains elements of both a simple pendulum and a one-dimensional spring-mass system. For specific energy values, the system demonstrates all the hallmarks of chaotic behavior and is sensitive to initial conditions.At very low and very high energy, there also appears to be regular motion. The motion of an elastic pendulum is governed by a set of coupled ordinary differential equations.This behavior suggests a complex interplay between energy states and system dynamics.
A proper reference frame in the theory of relativity is a particular form of accelerated reference frame, that is, a reference frame in which an accelerated observer can be considered as being at rest. It can describe phenomena in curved spacetime, as well as in "flat" Minkowski spacetime in which the spacetime curvature caused by the energy–momentum tensor can be disregarded. Since this article considers only flat spacetime—and uses the definition that special relativity is the theory of flat spacetime while general relativity is a theory of gravitation in terms of curved spacetime—it is consequently concerned with accelerated frames in special relativity.





































