In applied mathematics, Gabor atoms, or Gabor functions, are functions used in the analysis proposed by Dennis Gabor in 1946 in which a family of functions is built from translations and modulations of a generating function.
In 1946, [1] Dennis Gabor suggested the idea of using a granular system to produce sound. In his work, Gabor discussed the problems with Fourier analysis. Although he found the mathematics to be correct, it did not reflect the behaviour of sound in the world, because sounds, such as the sound of a siren, have variable frequencies over time. Another problem was the underlying supposition, as we use sine waves analysis, that the signal under concern has infinite duration even though sounds in real life have limited duration – see time–frequency analysis. Gabor applied ideas from quantum physics to sound, allowing an analogy between sound and quanta. He proposed a mathematical method to reduce Fourier analysis into cells. His research aimed at the information transmission through communication channels. Gabor saw in his atoms a possibility to transmit the same information but using less data. Instead of transmitting the signal itself it would be possible to transmit only the coefficients which represent the same signal using his atoms.
The Gabor function is defined by
where a and b are constants and g is a fixed function in L2(R), such that ||g|| = 1. Depending on , , and , a Gabor system may be a basis for L2(R), which is defined by translations and modulations. This is similar to a wavelet system, which may form a basis through dilating and translating a mother wavelet.
When one takes
one gets the Gabor transform.
In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
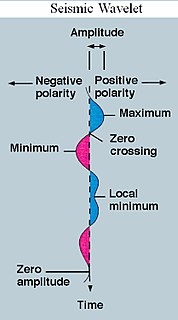
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one recorded by a seismograph or heart monitor. Generally, wavelets are intentionally crafted to have specific properties that make them useful for signal processing. Using a "reverse, shift, multiply and integrate" technique called convolution, wavelets can be combined with known portions of a damaged signal to extract information from the unknown portions.
The Fourier transform (FT) decomposes a function of time into its constituent frequencies. This is similar to the way a musical chord can be expressed in terms of the volumes and frequencies of its constituent notes. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of time. The Fourier transform of a function of time is itself a complex-valued function of frequency, whose magnitude (modulus) represents the amount of that frequency present in the original function, and whose argument is the phase offset of the basic sinusoid in that frequency. The Fourier transform is not limited to functions of time, but the domain of the original function is commonly referred to as the time domain. There is also an inverse Fourier transform that mathematically synthesizes the original function from its frequency domain representation.
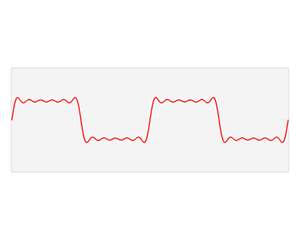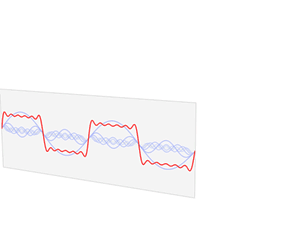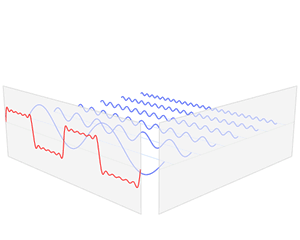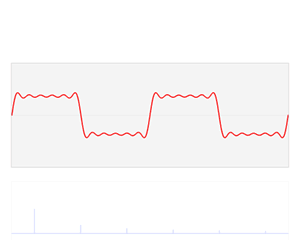
In mathematics, a Fourier series is a periodic function composed of harmonically related sinusoids, combined by a weighted summation. With appropriate weights, one cycle of the summation can be made to approximate an arbitrary function in that interval. As such, the summation is a synthesis of another function. The discrete-time Fourier transform is an example of Fourier series. The process of deriving the weights that describe a given function is a form of Fourier analysis. For functions on unbounded intervals, the analysis and synthesis analogies are Fourier transform and inverse transform.
In mathematics, the Gibbs phenomenon, discovered by Henry Wilbraham (1848) and rediscovered by J. Willard Gibbs (1899), is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity. The nth partial sum of the Fourier series has large oscillations near the jump, which might increase the maximum of the partial sum above that of the function itself. The overshoot does not die out as n increases, but approaches a finite limit. This sort of behavior was also observed by experimental physicists, but was believed to be due to imperfections in the measuring apparatuses.
The short-term Fourier transform (STFT), is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. In practice, the procedure for computing STFTs is to divide a longer time signal into shorter segments of equal length and then compute the Fourier transform separately on each shorter segment. This reveals the Fourier spectrum on each shorter segment. One then usually plots the changing spectra as a function of time, known as a spectrogram or waterfall plot.
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum of the square of a function is equal to the sum of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later applied to the Fourier series. It is also known as Rayleigh's energy theorem, or Rayleigh's identity, after John William Strutt, Lord Rayleigh.
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains simultaneously, using various time–frequency representations. Rather than viewing a 1-dimensional signal and some transform, time–frequency analysis studies a two-dimensional signal – a function whose domain is the two-dimensional real plane, obtained from the signal via a time–frequency transform.
Stransform as a time–frequency distribution was developed in 1994 for analyzing geophysics data. In this way, the S transform is a generalization of the short-time Fourier transform (STFT), extending the continuous wavelet transform and overcoming some of its disadvantages. For one, modulation sinusoids are fixed with respect to the time axis; this localizes the scalable Gaussian window dilations and translations in S transform. Moreover, the S transform doesn't have a cross-term problem and yields a better signal clarity than Gabor transform. However, the S transform has its own disadvantages: the clarity is worse than Wigner distribution function and Cohen's class distribution function.
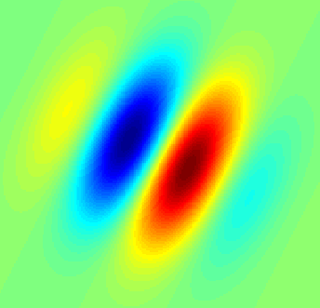
In image processing, a Gabor filter, named after Dennis Gabor, is a linear filter used for texture analysis, which means that it basically analyzes whether there are any specific frequency content in the image in specific directions in a localized region around the point or region of analysis. Frequency and orientation representations of Gabor filters are claimed by many contemporary vision scientists to be similar to those of the human visual system. They have been found to be particularly appropriate for texture representation and discrimination. In the spatial domain, a 2D Gabor filter is a Gaussian kernel function modulated by a sinusoidal plane wave.
In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.
The Wigner distribution function (WDF) is used in signal processing as a transform in time-frequency analysis.
In mathematics, the Balian–Low theorem in Fourier analysis is named for Roger Balian and Francis E. Low. The theorem states that there is no well-localized window function g either in time or frequency for an exact Gabor frame.
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window function, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal x(t) is defined by this formula:
In the mathematics of signal processing, the harmonic wavelet transform, introduced by David Edward Newland in 1993, is a wavelet-based linear transformation of a given function into a time-frequency representation. It combines advantages of the short-time Fourier transform and the continuous wavelet transform. It can be expressed in terms of repeated Fourier transforms, and its discrete analogue can be computed efficiently using a fast Fourier transform algorithm.
The cone-shape distribution function, also known as the Zhao–Atlas–Marks time-frequency distribution,, is one of the members of Cohen's class distribution function. It was first proposed by Yunxin Zhao, Les E. Atlas, and Robert J. Marks II in 1990. The distribution's name stems from the twin cone shape of the distribution's kernel function on the plane. The advantage of the cone kernel function is that it can completely remove the cross-term between two components having the same center frequency. Cross-term results from components with the same time center, however, cannot be completely removed by the cone-shaped kernel.
In mathematics, the Hausdorff−Young inequality bounds the Lq-norm of the Fourier coefficients of a periodic function for q ≥ 2. William Henry Young (1913) proved the inequality for some special values of q, and Hausdorff (1923) proved it in general. More generally the inequality also applies to the Fourier transform of a function on a locally compact group, such as Rn, and in this case Babenko (1961) and Beckner (1975) gave a sharper form of it called the Babenko–Beckner inequality.
Overcompleteness is a concept from linear algebra that is widely used in mathematics, computer science, engineering, and statistics. It was introduced by R. J. Duffin and A. C. Schaeffer in 1952.
Hans Georg Feichtinger is an Austrian mathematician. He is Professor in the mathematical faculty of the University of Vienna. He is editor-in-chief of the Journal of Fourier Analysis and Applications (JFAA) and associate editor to several other journals. He is one of the founders and head of the Numerical Harmonic Analysis Group (NuHAG) at University of Vienna. Today Feichtinger's main field of research is harmonic analysis with a focus on time-frequency analysis.
In mathematical analysis, the Szegő limit theorems describe the asymptotic behaviour of the determinants of large Toeplitz matrices. They were first proved by Gábor Szegő.
