Game tree

Last updated January 16, 2024

In the context of combinatorial game theory, which typically studies sequential games with perfect information, a game tree is a graph representing all possible game states within such a game. Such games include well-known ones such as chess, checkers, Go, and tic-tac-toe. This can be used to measure the complexity of a game, as it represents all the possible ways a game can pan out. Due to the large game trees of complex games such as chess, algorithms that are designed to play this class of games will use partial game trees, which makes computation feasible on modern computers. Various methods exist to solve game trees. If a complete game tree can be generated, a deterministic algorithm, such as backward induction or retrograde analysis can be used. Randomized algorithms and minmax algorithms such as MCTS can be used in cases where a complete game tree is not feasible.

Understanding the game tree

To better understand the game tree, it can be thought of as a technique for analyzing adversarial games, which determine the actions that player takes to win the game. In game theory, a game tree is a directed graph whose nodes are positions in a game (e.g., the arrangement of the pieces in a board game) and whose edges are moves (e.g., to move pieces from one position on a board to another).^[1]

The complete game tree for a game is the game tree starting at the initial position and containing all possible moves from each position; the complete tree is the same tree as that obtained from the extensive-form game representation. To be more specific, the complete game is a norm for the game in game theory. Which can clearly express many important aspects. For example, the sequence of actions that stakeholders may take, their choices at each decision point, information about actions taken by other stakeholders when each stakeholder makes a decision, and the benefits of all possible game results.^[2]

The first two plies of the game tree for tic-tac-toe. Tic-tac-toe-game-tree.svg — The first two plies of the game tree for tic-tac-toe.

The diagram shows the first two levels, or plies , in the game tree for tic-tac-toe. The rotations and reflections of positions are equivalent, so the first player has three choices of move: in the center, at the edge, or in the corner. The second player has two choices for the reply if the first player played in the center, otherwise five choices. And so on.

The number of leaf nodes in the complete game tree is the number of possible different ways the game can be played. For example, the game tree for tic-tac-toe has 255,168 leaf nodes.

Game trees are important in artificial intelligence because one way to pick the best move in a game is to search the game tree using any of numerous tree search algorithms, combined with minimax-like rules to prune the tree. The game tree for tic-tac-toe is easily searchable, but the complete game trees for larger games like chess are much too large to search. Instead, a chess-playing program searches a partial game tree: typically as many plies from the current position as it can search in the time available. Except for the case of "pathological" game trees^[3] (which seem to be quite rare in practice), increasing the search depth (i.e., the number of plies searched) generally improves the chance of picking the best move.

Two-person games can also be represented as and-or trees. For the first player to win a game, there must exist a winning move for all moves of the second player. This is represented in the and-or tree by using disjunction to represent the first player's alternative moves and using conjunction to represent all of the second player's moves.

Solving game trees

Deterministic algorithm version

An arbitrary game tree that has been fully colored Arbitrary-gametree-solved.svg — An arbitrary game tree that has been fully colored

With a complete game tree, it is possible to "solve" the game – that is to say, find a sequence of moves that either the first or second player can follow that will guarantee the best possible outcome for that player (usually a win or a tie). The deterministic algorithm (which is generally called backward induction or retrograde analysis) can be described recursively as follows.

Color the final ply of the game tree so that all wins for player 1 are colored one way (Blue in the diagram), all wins for player 2 are colored another way (Red in the diagram), and all ties are colored a third way (Grey in the diagram).
Look at the next ply up. If there exists a node colored opposite as the current player, color this node for that player as well. If all immediately lower nodes are colored for the same player, color this node for the same player as well. Otherwise, color this node a tie.
Repeat for each ply, moving upwards, until all nodes are colored. The color of the root node will determine the nature of the game.

The diagram shows a game tree for an arbitrary game, colored using the above algorithm.

It is usually possible to solve a game (in this technical sense of "solve") using only a subset of the game tree, since in many games a move need not be analyzed if there is another move that is better for the same player (for example alpha-beta pruning can be used in many deterministic games).

Any subtree that can be used to solve the game is known as a decision tree, and the sizes of decision trees of various shapes are used as measures of game complexity.^[4]

Randomized algorithms version

Randomized algorithms can be used in solving game trees. There are two main advantages in this type of implementation: speed and practicality. Whereas a deterministic version of solving game trees can be done in $Ο (n)$ , the following randomized algorithm has an expected run time of $θ (n 0.792)$ if every node in the game tree has degree 2. Moreover, it is practical because randomized algorithms are capable of "foiling an enemy", meaning an opponent cannot beat the system of game trees by knowing the algorithm used to solve the game tree because the order of solving is random.

The following is an implementation of randomized game tree solution algorithm:^[5]

defgt_eval_rand(u)->bool:"""Returns True if this node evaluates to a win, otherwise False"""ifu.leaf:returnu.winelse:random_children=(gt_eval_rand(child)forchildinrandom_order(u.children))ifu.op=="OR":returnany(random_children)ifu.op=="AND":returnall(random_children)

The algorithm makes use of the idea of "short-circuiting": if the root node is considered an "OR" operator, then once one True is found, the root is classified as True; conversely, if the root node is considered an "AND" operator then once one False is found, the root is classified as False.

^[6]

Related Research Articles

Minmax is a decision rule used in artificial intelligence, decision theory, game theory, statistics, and philosophy for minimizing the possible loss for a worst case scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.

Tic-tac-toe, noughts and crosses, or Xs and Os is a paper-and-pencil game for two players who take turns marking the spaces in a three-by-three grid with X or O. The player who succeeds in placing three of their marks in a horizontal, vertical, or diagonal row is the winner. It is a solved game, with a forced draw assuming best play from both players.

A solved game is a game whose outcome can be correctly predicted from any position, assuming that both players play perfectly. This concept is usually applied to abstract strategy games, and especially to games with full information and no element of chance; solving such a game may use combinatorial game theory and/or computer assistance.

Computer chess includes both hardware and software capable of playing chess. Computer chess provides opportunities for players to practice even in the absence of human opponents, and also provides opportunities for analysis, entertainment and training. Computer chess applications that play at the level of a chess grandmaster or higher are available on hardware from supercomputers to smart phones. Standalone chess-playing machines are also available. Stockfish, Leela Chess Zero, GNU Chess, Fruit, and other free open source applications are available for various platforms.

Alpha–beta pruning is a search algorithm that seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree. It is an adversarial search algorithm used commonly for machine playing of two-player combinatorial games. It stops evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.

The horizon effect, also known as the horizon problem, is a problem in artificial intelligence whereby, in many games, the number of possible states or positions is immense and computers can only feasibly search a small portion of them, typically a few plies down the game tree. Thus, for a computer searching only five plies, there is a possibility that it will make a detrimental move, but the effect is not visible because the computer does not search to the depth of the error.

Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position that the players take turns changing in defined ways or moves to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field.

Combinatorial game theory measures game complexity in several ways:

State-space complexity,
Game tree size,
Decision complexity,
Game-tree complexity,
Computational complexity.

In combinatorial game theory, the strategy-stealing argument is a general argument that shows, for many two-player games, that the second player cannot have a guaranteed winning strategy. The strategy-stealing argument applies to any symmetric game in which an extra move can never be a disadvantage. A key property of a strategy-stealing argument is that it proves that the first player can win the game without actually constructing such a strategy. So, although it might prove the existence of a winning strategy, the proof gives no information about what that strategy is.

In game theory, an extensive-form game is a specification of a game allowing for the explicit representation of a number of key aspects, like the sequencing of players' possible moves, their choices at every decision point, the information each player has about the other player's moves when they make a decision, and their payoffs for all possible game outcomes. Extensive-form games also allow for the representation of incomplete information in the form of chance events modeled as "moves by nature". Extensive-form representations differ from normal-form in that they provide a more complete description of the game in question, whereas normal-form simply boils down the game into a payoff matrix.

Negamax search is a variant form of minimax search that relies on the zero-sum property of a two-player game.

In game theory, a sequential game is a game where one player chooses their action before the others choose theirs. The other players must have information on the first player's choice so that the difference in time has no strategic effect. Sequential games are governed by the time axis and represented in the form of decision trees.

An and–or tree is a graphical representation of the reduction of problems to conjunctions and disjunctions of subproblems.

In computer science, B* is a best-first graph search algorithm that finds the least-cost path from a given initial node to any goal node. First published by Hans Berliner in 1979, it is related to the A* search algorithm.

<span class="mw-page-title-main">Zillions of Games</span> General game playing software

Zillions of Games is a commercial general game playing system developed by Jeff Mallett and Mark Lefler in 1998. The game rules are specified with S-expressions, Zillions rule language. It was designed to handle mostly abstract strategy board games or puzzles. After parsing the rules of the game, the system's artificial intelligence can automatically play one or more players. It treats puzzles as solitaire games and its AI can be used to solve them.

<span class="mw-page-title-main">First-player and second-player win</span>

In combinatorial game theory, a two-player deterministic perfect information turn-based game is a first-player-win if with perfect play the first player to move can always force a win. Similarly, a game is second-player-win if with perfect play the second player to move can always force a win. With perfect play, if neither side can force a win, the game is a draw.

In computer science, Monte Carlo tree search (MCTS) is a heuristic search algorithm for some kinds of decision processes, most notably those employed in software that plays board games. In that context MCTS is used to solve the game tree.

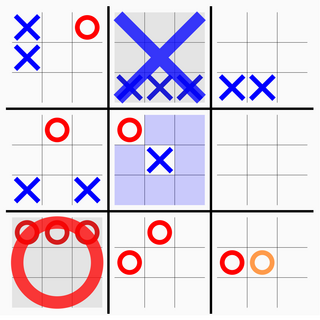
Ultimate tic-tac-toe is a board game composed of nine tic-tac-toe boards arranged in a 3 × 3 grid. Players take turns playing on the smaller tic-tac-toe boards until one of them wins on the larger board. Compared to traditional tic-tac-toe, strategy in this game is conceptually more difficult and has proven more challenging for computers.

Tic-tac-toe is an instance of an m,n,k-game, where two players alternate taking turns on an m×n board until one of them gets k in a row. Harary's generalized tic-tac-toe is an even broader generalization. The game can also be generalized as a n^d game. The game can be generalised even further from the above variants by playing on an arbitrary hypergraph where rows are hyperedges and cells are vertices.

References

↑ Zuckerman, Inon; Wilson, Brandon; Nau, Dana S. (2018). "Avoiding game-tree pathology in 2-player adversarial search". Computational Intelligence. 34 (2): 542–561. doi:10.1111/coin.12162. ISSN 1467-8640. S2CID 46926187.
↑ Huang, Zishuo; Yu, Hang; Chu, Xiangyang; Peng, Zhenwei (2018-05-01). "A novel optimization model based on game tree for multi-energy conversion systems". Energy. 150: 109–121. doi:10.1016/j.energy.2018.02.091. ISSN 0360-5442.
↑ Nau, Dana (1982). "An investigation of the causes of pathology in games". Artificial Intelligence. 19 (3): 257–278. doi:10.1016/0004-3702(82)90002-9.
↑ Victor Allis (1994). Searching for Solutions in Games and Artificial Intelligence (PDF). Ph.D. Thesis, University of Limburg, Maastricht, The Netherlands. ISBN 90-900748-8-0.
↑ Daniel Roche (2013). SI486D: Randomness in Computing, Game Trees Unit. United States Naval Academy, Computer Science Department.
↑ Pekař, Libor; Matušů, Radek; Andrla, Jiří; Litschmannová, Martina (September 2020). "Review of Kalah Game Research and the Proposition of a Novel Heuristic–Deterministic Algorithm Compared to Tree-Search Solutions and Human Decision-Making". Informatics. 7 (3): 34. doi: 10.3390/informatics7030034 . hdl: 10084/142398 .