Game complexity

Last updated

Combinatorial game theory measures game complexity in several ways:

Contents

  1. State-space complexity (the number of legal game positions from the initial position),
  2. Game tree size (total number of possible games),
  3. Decision complexity (number of leaf nodes in the smallest decision tree for initial position),
  4. Game-tree complexity (number of leaf nodes in the smallest full-width decision tree for initial position),
  5. Computational complexity (asymptotic difficulty of a game as it grows arbitrarily large).

These measures involve understanding game positions, possible outcomes, and computation required for various game scenarios.

Measures of game complexity

State-space complexity

The state-space complexity of a game is the number of legal game positions reachable from the initial position of the game. [1]

When this is too hard to calculate, an upper bound can often be computed by also counting (some) illegal positions, meaning positions that can never arise in the course of a game.

Game tree size

The game tree size is the total number of possible games that can be played: the number of leaf nodes in the game tree rooted at the game's initial position.

The game tree is typically vastly larger than the state space because the same positions can occur in many games by making moves in a different order (for example, in a tic-tac-toe game with two X and one O on the board, this position could have been reached in two different ways depending on where the first X was placed). An upper bound for the size of the game tree can sometimes be computed by simplifying the game in a way that only increases the size of the game tree (for example, by allowing illegal moves) until it becomes tractable.

For games where the number of moves is not limited (for example by the size of the board, or by a rule about repetition of position) the game tree is generally infinite.

Decision trees

The next two measures use the idea of a decision tree , which is a subtree of the game tree, with each position labelled with "player A wins", "player B wins" or "drawn", if that position can be proved to have that value (assuming best play by both sides) by examining only other positions in the graph. (Terminal positions can be labelled directly; a position with player A to move can be labelled "player A wins" if any successor position is a win for A, or labelled "player B wins" if all successor positions are wins for B, or labelled "draw" if all successor positions are either drawn or wins for B. And correspondingly for positions with B to move.)

Decision complexity

Decision complexity of a game is the number of leaf nodes in the smallest decision tree that establishes the value of the initial position.

Game-tree complexity

The game-tree complexity of a game is the number of leaf nodes in the smallest full-width decision tree that establishes the value of the initial position. [1] A full-width tree includes all nodes at each depth.

This is an estimate of the number of positions one would have to evaluate in a minimax search to determine the value of the initial position.

It is hard even to estimate the game-tree complexity, but for some games an approximation can be given by raising the game's average branching factor b to the power of the number of plies d in an average game, or:

.

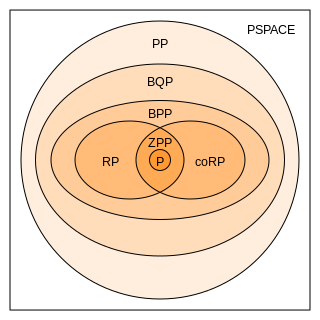
Computational complexity

The computational complexity of a game describes the asymptotic difficulty of a game as it grows arbitrarily large, expressed in big O notation or as membership in a complexity class. This concept doesn't apply to particular games, but rather to games that have been generalized so they can be made arbitrarily large, typically by playing them on an n-by-n board. (From the point of view of computational complexity a game on a fixed size of board is a finite problem that can be solved in O(1), for example by a look-up table from positions to the best move in each position.)

The asymptotic complexity is defined by the most efficient (in terms of whatever computational resource one is considering) algorithm for solving the game; the most common complexity measure (computation time) is always lower-bounded by the logarithm of the asymptotic state-space complexity, since a solution algorithm must work for every possible state of the game. It will be upper-bounded by the complexity of any particular algorithm that works for the family of games. Similar remarks apply to the second-most commonly used complexity measure, the amount of space or computer memory used by the computation. It is not obvious that there is any lower bound on the space complexity for a typical game, because the algorithm need not store game states; however many games of interest are known to be PSPACE-hard, and it follows that their space complexity will be lower-bounded by the logarithm of the asymptotic state-space complexity as well (technically the bound is only a polynomial in this quantity; but it is usually known to be linear).

Example: tic-tac-toe (noughts and crosses)

For tic-tac-toe, a simple upper bound for the size of the state space is 39 = 19,683. (There are three states for each cell and nine cells.) This count includes many illegal positions, such as a position with five crosses and no noughts, or a position in which both players have a row of three. A more careful count, removing these illegal positions, gives 5,478. [2] [3] And when rotations and reflections of positions are considered identical, there are only 765 essentially different positions.

To bound the game tree, there are 9 possible initial moves, 8 possible responses, and so on, so that there are at most 9! or 362,880 total games. However, games may take less than 9 moves to resolve, and an exact enumeration gives 255,168 possible games. When rotations and reflections of positions are considered the same, there are only 26,830 possible games.

The computational complexity of tic-tac-toe depends on how it is generalized. A natural generalization is to m,n,k-games: played on an m by n board with winner being the first player to get k in a row. It is immediately clear that this game can be solved in DSPACE(mn) by searching the entire game tree. This places it in the important complexity class PSPACE. With some more work it can be shown to be PSPACE-complete. [4]

Complexities of some well-known games

Due to the large size of game complexities, this table gives the ceiling of their logarithm to base 10. (In other words, the number of digits). All of the following numbers should be considered with caution: seemingly-minor changes to the rules of a game can change the numbers (which are often rough estimates anyway) by tremendous factors, which might easily be much greater than the numbers shown.

Note: ordered by game tree size

GameBoard size

(positions)

State-space complexity

(as log to base 10)

Game-tree complexity

(as log to base 10)

Average game length

(plies)

Branching factorRef Complexity class of suitable generalized game
Tic-tac-toe 93594 PSPACE-complete [5]
Sim 1538143.7 PSPACE-complete [6]
Pentominoes 6412181075 [7] [8]  ?, but in PSPACE
Kalah [9] 14131850 [7] Generalization is unclear
Connect Four 421321364 [1] [10]  ?, but in PSPACE
Domineering (8 × 8)641527308 [7]  ?, but in PSPACE; in P for certain dimensions [11]
Congkak 141533 [7]
English draughts (8x8) (checkers) 3220 or 1840702.8 [1] [12] [13] EXPTIME-complete [14]
Awari [15] 121232603.5 [1] Generalization is unclear
Qubic 6430342054.2 [1] PSPACE-complete [5]
Double dummy bridge [nb 1] (52)<17<40525.6PSPACE-complete [16]
Fanorona 4521464411 [17]  ?, but in EXPTIME
Nine men's morris 2410505010 [1]  ?, but in EXPTIME
Tablut 8127 [18]
International draughts (10x10) 503054904 [1] EXPTIME-complete [14]
Chinese checkers (2 sets)12123180 [19] EXPTIME-complete [20]
Chinese checkers (6 sets)12178600 [19] EXPTIME-complete [20]
Reversi (Othello)6428585810 [1] PSPACE-complete [21]
OnTop (2p base game)7288623123.77 [22]
Lines of Action 6423644429 [23]  ?, but in EXPTIME
Gomoku (15x15, freestyle)2251057030210 [1] PSPACE-complete [5]
Hex (11x11) 12157985096 [7] PSPACE-complete [5]
Chess 64441237035 [24] EXPTIME-complete (without 50-move drawing rule) [25]
Bejeweled and Candy Crush (8x8)64<5070 [26] NP-hard
GIPF 37251329029.3 [27]
Connect6 3611721403046000 [28] PSPACE-complete [29]
Backgammon 282014455250 [30] Generalization is unclear
Xiangqi 90401509538 [1] [31] [32]  ?, believed to be EXPTIME-complete
Abalone 61251548760 [33] [34] PSPACE-hard, and in EXPTIME
Havannah 27112715766240 [7] [35] PSPACE-complete [36]
Twixt 57214015960452 [37]
Janggi 904416010040 [32]  ?, believed to be EXPTIME-complete
Quoridor 81421629160 [38]  ?, but in PSPACE
Carcassonne (2p base game)72>401957155 [39] Generalization is unclear
Amazons (10x10) 1004021284374 or 299 [40] [41] [42] PSPACE-complete [43]
Shogi 817122611592 [31] [44] EXPTIME-complete [45]
Thurn and Taxis (2 player)336624056879 [46]
Go (19x19) 361170360150250 [1] [47] [48] EXPTIME-complete (without the superko rule) [49]
Arimaa 64434029217281 [50] [51] [52]  ?, but in EXPTIME
Stratego 9211553538121.739 [53]
Infinite chess infiniteinfiniteinfiniteinfiniteinfinite [54] Un­known, but mate-in-n is decidable [55]
Magic: The Gathering [56] AH-hard [57]
Wordle 512,9726 [58] NP-hard, unknown if PSPACE-complete with parametization.

Notes

  1. ↑ Double dummy bridge (i.e., double dummy problems in the context of contract bridge) is not a proper board game but has a similar game tree, and is studied in computer bridge. The bridge table can be regarded as having one slot for each player and trick to play a card in, which corresponds to board size 52. Game-tree complexity is a very weak upper bound: 13! to the power of 4 players regardless of legality. State-space complexity is for one given deal; likewise regardless of legality but with many transpositions eliminated. The last 4 plies are always forced moves with branching factor 1.

Related Research Articles

<span class="mw-page-title-main">BQP</span> Computational complexity class of problems

In computational complexity theory, bounded-error quantum polynomial time (BQP) is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances. It is the quantum analogue to the complexity class BPP.

In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

<span class="mw-page-title-main">Hex (board game)</span> Abstract strategy board game

Hex is a two player abstract strategy board game in which players attempt to connect opposite sides of a rhombus-shaped board made of hexagonal cells. Hex was invented by mathematician and poet Piet Hein in 1942 and later rediscovered and popularized by John Nash.

In computational complexity theory, a decision problem is PSPACE-complete if it can be solved using an amount of memory that is polynomial in the input length and if every other problem that can be solved in polynomial space can be transformed to it in polynomial time. The problems that are PSPACE-complete can be thought of as the hardest problems in PSPACE, the class of decision problems solvable in polynomial space, because a solution to any one such problem could easily be used to solve any other problem in PSPACE.

In computational complexity theory, the complexity class EXPTIME (sometimes called EXP or DEXPTIME) is the set of all decision problems that are solvable by a deterministic Turing machine in exponential time, i.e., in O(2p(n)) time, where p(n) is a polynomial function of n.

A solved game is a game whose outcome can be correctly predicted from any position, assuming that both players play perfectly. This concept is usually applied to abstract strategy games, and especially to games with full information and no element of chance; solving such a game may use combinatorial game theory and/or computer assistance.

<span class="mw-page-title-main">Evaluation function</span> Function in a computer game-playing program that evaluates a game position

An evaluation function, also known as a heuristic evaluation function or static evaluation function, is a function used by game-playing computer programs to estimate the value or goodness of a position in a game tree. Most of the time, the value is either a real number or a quantized integer, often in nths of the value of a playing piece such as a stone in go or a pawn in chess, where n may be tenths, hundredths or other convenient fraction, but sometimes, the value is an array of three values in the unit interval, representing the win, draw, and loss percentages of the position.

In the context of combinatorial game theory, which typically studies sequential games with perfect information, a game tree is a graph representing all possible game states within such a game. Such games include well-known ones such as chess, checkers, Go, and tic-tac-toe. This can be used to measure the complexity of a game, as it represents all the possible ways a game can pan out. Due to the large game trees of complex games such as chess, algorithms that are designed to play this class of games will use partial game trees, which makes computation feasible on modern computers. Various methods exist to solve game trees. If a complete game tree can be generated, a deterministic algorithm, such as backward induction or retrograde analysis can be used. Randomized algorithms and minmax algorithms such as MCTS can be used in cases where a complete game tree is not feasible.

In quantum computing, a quantum algorithm is an algorithm that runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer. Although all classical algorithms can also be performed on a quantum computer, the term quantum algorithm is generally reserved for algorithms that seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition or quantum entanglement.

<span class="mw-page-title-main">Generalized game</span> Game generalized so that it can be played on a board or grid of any size

In computational complexity theory, a generalized game is a game or puzzle that has been generalized so that it can be played on a board or grid of any size. For example, generalized chess is the game of chess played on an board, with pieces on each side. Generalized Sudoku includes Sudokus constructed on an grid.

<span class="mw-page-title-main">Shannon number</span> Estimate of number of possible chess games

The Shannon number, named after the American mathematician Claude Shannon, is a conservative lower bound of the game-tree complexity of chess of 10120, based on an average of about 103 possibilities for a pair of moves consisting of a move for White followed by a move for Black, and a typical game lasting about 40 such pairs of moves.

<span class="mw-page-title-main">Go and mathematics</span> Calculations of the game complexity of go

The game of Go is one of the most popular games in the world. As a result of its elegant and simple rules, the game has long been an inspiration for mathematical research. Shen Kuo, an 11th century Chinese scholar, estimated in his Dream Pool Essays that the number of possible board positions is around 10172. In more recent years, research of the game by John H. Conway led to the development of the surreal numbers and contributed to development of combinatorial game theory (with Go Infinitesimals being a specific example of its use in Go).

In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A (fully) quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified, using either existential or universal quantifiers, at the beginning of the sentence. Such a formula is equivalent to either true or false. If such a formula evaluates to true, then that formula is in the language TQBF. It is also known as QSAT.

Quantum complexity theory is the subfield of computational complexity theory that deals with complexity classes defined using quantum computers, a computational model based on quantum mechanics. It studies the hardness of computational problems in relation to these complexity classes, as well as the relationship between quantum complexity classes and classical complexity classes.

In algorithmic game theory, a succinct game or a succinctly representable game is a game which may be represented in a size much smaller than its normal form representation. Without placing constraints on player utilities, describing a game of players, each facing strategies, requires listing utility values. Even trivial algorithms are capable of finding a Nash equilibrium in a time polynomial in the length of such a large input. A succinct game is of polynomial type if in a game represented by a string of length n the number of players, as well as the number of strategies of each player, is bounded by a polynomial in n.

Solving chess consists of finding an optimal strategy for the game of chess; that is, one by which one of the players can always force a victory, or either can force a draw. It is also related to more generally solving chess-like games such as Capablanca chess and infinite chess. In a weaker sense, solving chess may refer to proving which one of the three possible outcomes is the result of two perfect players, without necessarily revealing the optimal strategy itself.

In computational complexity theory, and more specifically in the analysis of algorithms with integer data, the transdichotomous model is a variation of the random-access machine in which the machine word size is assumed to match the problem size. The model was proposed by Michael Fredman and Dan Willard, who chose its name "because the dichotomy between the machine model and the problem size is crossed in a reasonable manner."

In computer science, Monte Carlo tree search (MCTS) is a heuristic search algorithm for some kinds of decision processes, most notably those employed in software that plays board games. In that context MCTS is used to solve the game tree.

In discrete mathematics and theoretical computer science, reconfiguration problems are computational problems involving reachability or connectivity of state spaces.

References

  1. 1 2 3 4 5 6 7 8 9 10 11 12 Victor Allis (1994). Searching for Solutions in Games and Artificial Intelligence (PDF) (Ph.D. thesis). University of Limburg, Maastricht, The Netherlands. ISBN   90-900748-8-0.
  2. ↑ "combinatorics - TicTacToe State Space Choose Calculation". Mathematics Stack Exchange. Retrieved 2020-04-08.
  3. ↑ T, Brian (October 20, 2018). "Btsan/generate_tictactoe". GitHub . Retrieved 2020-04-08.
  4. ↑ Stefan Reisch (1980). "Gobang ist PSPACE-vollständig (Gobang is PSPACE-complete)". Acta Informatica. 13 (1): 59–66. doi:10.1007/bf00288536. S2CID   21455572.
  5. 1 2 3 4 Stefan Reisch (1981). "Hex ist PSPACE-vollständig (Hex is PSPACE-complete)". Acta Inform (15): 167–191.
  6. ↑ Slany, Wolfgang (2000). "The complexity of graph Ramsey games". In Marsland, T. Anthony; Frank, Ian (eds.). Computers and Games, Second International Conference, CG 2000, Hamamatsu, Japan, October 26-28, 2000, Revised Papers. Lecture Notes in Computer Science. Vol. 2063. Springer. pp. 186–203. doi:10.1007/3-540-45579-5_12.
  7. 1 2 3 4 5 6 H. J. van den Herik; J. W. H. M. Uiterwijk; J. van Rijswijck (2002). "Games solved: Now and in the future". Artificial Intelligence. 134 (1–2): 277–311. doi: 10.1016/S0004-3702(01)00152-7 .
  8. ↑ Orman, Hilarie K. (1996). "Pentominoes: a first player win" (PDF). In Nowakowski, Richard J. (ed.). Games of No Chance: Papers from the Combinatorial Games Workshop held in Berkeley, CA, July 11–21, 1994. Mathematical Sciences Research Institute Publications. Vol. 29. Cambridge University Press. pp. 339–344. ISBN   0-521-57411-0. MR   1427975.
  9. ↑ See van den Herik et al for rules.
  10. ↑ John Tromp (2010). "John's Connect Four Playground".
  11. ↑ Lachmann, Michael; Moore, Cristopher; Rapaport, Ivan (2002). "Who wins Domineering on rectangular boards?". In Nowakowski, Richard (ed.). More Games of No Chance: Proceedings of the 2nd Combinatorial Games Theory Workshop held in Berkeley, CA, July 24–28, 2000. Mathematical Sciences Research Institute Publications. Vol. 42. Cambridge University Press. pp. 307–315. ISBN   0-521-80832-4. MR   1973019.
  12. ↑ Jonathan Schaeffer; et al. (July 6, 2007). "Checkers is Solved". Science. 317 (5844): 1518–1522. Bibcode:2007Sci...317.1518S. doi: 10.1126/science.1144079 . PMID   17641166. S2CID   10274228.
  13. ↑ Schaeffer, Jonathan (2007). "Game over: Black to play and draw in checkers" (PDF). ICGA Journal . 30 (4): 187–197. doi:10.3233/ICG-2007-30402. Archived from the original (PDF) on 2016-04-03.
  14. 1 2 J. M. Robson (1984). "N by N checkers is Exptime complete". SIAM Journal on Computing . 13 (2): 252–267. doi:10.1137/0213018.
  15. ↑ See Allis 1994 for rules
  16. ↑ Bonnet, Edouard; Jamain, Florian; Saffidine, Abdallah (2013). "On the complexity of trick-taking card games". In Rossi, Francesca (ed.). IJCAI 2013, Proceedings of the 23rd International Joint Conference on Artificial Intelligence, Beijing, China, August 3-9, 2013. IJCAI/AAAI. pp. 482–488.
  17. ↑ M.P.D. Schadd; M.H.M. Winands; J.W.H.M. Uiterwijk; H.J. van den Herik; M.H.J. Bergsma (2008). "Best Play in Fanorona leads to Draw" (PDF). New Mathematics and Natural Computation . 4 (3): 369–387. doi:10.1142/S1793005708001124.
  18. ↑ Andrea Galassi (2018). "An Upper Bound on the Complexity of Tablut".
  19. 1 2 G.I. Bell (2009). "The Shortest Game of Chinese Checkers and Related Problems". Integers. 9. arXiv: 0803.1245 . Bibcode:2008arXiv0803.1245B. doi:10.1515/INTEG.2009.003. S2CID   17141575.
  20. 1 2 Kasai, Takumi; Adachi, Akeo; Iwata, Shigeki (1979). "Classes of pebble games and complete problems". SIAM Journal on Computing. 8 (4): 574–586. doi:10.1137/0208046. MR   0573848. Proves completeness of the generalization to arbitrary graphs.
  21. ↑ Iwata, Shigeki; Kasai, Takumi (1994). "The Othello game on an board is PSPACE-complete". Theoretical Computer Science. 123 (2): 329–340. doi: 10.1016/0304-3975(94)90131-7 . MR   1256205.
  22. ↑ Robert Briesemeister (2009). Analysis and Implementation of the Game OnTop (PDF) (Thesis). Maastricht University, Dept of Knowledge Engineering.
  23. ↑ Mark H.M. Winands (2004). Informed Search in Complex Games (PDF) (Ph.D. thesis). Maastricht University, Maastricht, The Netherlands. ISBN   90-5278-429-9.
  24. ↑ The size of the state space and game tree for chess were first estimated in Claude Shannon (1950). "Programming a Computer for Playing Chess" (PDF). Philosophical Magazine. 41 (314). Archived from the original (PDF) on 2010-07-06. Shannon gave estimates of 1043 and 10120 respectively, smaller than the upper bound in the table, which is detailed in Shannon number.
  25. ↑ Fraenkel, Aviezri S.; Lichtenstein, David (1981). "Computing a perfect strategy for chess requires time exponential in ". Journal of Combinatorial Theory, Series A . 31 (2): 199–214. doi: 10.1016/0097-3165(81)90016-9 . MR   0629595.
  26. ↑ Gualà, Luciano; Leucci, Stefano; Natale, Emanuele (2014). "Bejeweled, Candy Crush and other match-three games are (NP-)hard". 2014 IEEE Conference on Computational Intelligence and Games, CIG 2014, Dortmund, Germany, August 26-29, 2014. IEEE. pp. 1–8. arXiv: 1403.5830 . doi:10.1109/CIG.2014.6932866.
  27. ↑ Diederik Wentink (2001). Analysis and Implementation of the game Gipf (PDF) (Thesis). Maastricht University.
  28. ↑ Chang-Ming Xu; Ma, Z.M.; Jun-Jie Tao; Xin-He Xu (2009). "Enhancements of proof number search in connect6". 2009 Chinese Control and Decision Conference. p. 4525. doi:10.1109/CCDC.2009.5191963. ISBN   978-1-4244-2722-2. S2CID   20960281.
  29. ↑ Hsieh, Ming Yu; Tsai, Shi-Chun (October 1, 2007). "On the fairness and complexity of generalized k -in-a-row games". Theoretical Computer Science. 385 (1–3): 88–100. doi: 10.1016/j.tcs.2007.05.031 . Retrieved 2018-04-12– via dl.acm.org.
  30. ↑ Tesauro, Gerald (May 1, 1992). "Practical issues in temporal difference learning". Machine Learning. 8 (3–4): 257–277. doi: 10.1007/BF00992697 .
  31. 1 2 Shi-Jim Yen, Jr-Chang Chen; Tai-Ning Yang; Shun-Chin Hsu (March 2004). "Computer Chinese Chess" (PDF). International Computer Games Association Journal. 27 (1): 3–18. doi:10.3233/ICG-2004-27102. S2CID   10336286. Archived from the original (PDF) on 2007-06-14.
  32. 1 2 Donghwi Park (2015). "Space-state complexity of Korean chess and Chinese chess". arXiv: 1507.06401 [math.GM].
  33. ↑ Chorus, Pascal. "Implementing a Computer Player for Abalone Using Alpha-Beta and Monte-Carlo Search" (PDF). Dept of Knowledge Engineering, Maastricht University. Retrieved 2012-03-29.
  34. ↑ Kopczynski, Jacob S (2014). Pushy Computing: Complexity Theory and the Game Abalone (Thesis). Reed College.
  35. ↑ Joosten, B. "Creating a Havannah Playing Agent" (PDF). Retrieved 2012-03-29.
  36. ↑ E. Bonnet; F. Jamain; A. Saffidine (March 25, 2014). "Havannah and TwixT are PSPACE-complete". arXiv: 1403.6518 [cs.CC].
  37. ↑ Kevin Moesker (2009). Txixt: Theory, Analysis, and Implementation (PDF) (Thesis). Faculty of Humanities and Sciences of Maastricht University.
  38. ↑ Lisa Glendenning (May 2005). Mastering Quoridor (PDF). Computer Science (B.Sc. thesis). University of New Mexico. Archived from the original (PDF) on 2012-03-15.
  39. ↑ Cathleen Heyden (2009). Implementing a Computer Player for Carcassonne (PDF) (Thesis). Maastricht University, Dept of Knowledge Engineering.
  40. ↑ The lower branching factor is for the second player.
  41. ↑ Kloetzer, Julien; Iida, Hiroyuki; Bouzy, Bruno (2007). "The Monte-Carlo approach in Amazons" (PDF). Computer Games Workshop, Amsterdam, the Netherlands, 15-17 June 2007. pp. 185–192.
  42. ↑ P. P. L. M. Hensgens (2001). "A Knowledge-Based Approach of the Game of Amazons" (PDF). Universiteit Maastricht, Institute for Knowledge and Agent Technology.
  43. ↑ R. A. Hearn (February 2, 2005). "Amazons is PSPACE-complete". arXiv: cs.CC/0502013 .
  44. ↑ Hiroyuki Iida; Makoto Sakuta; Jeff Rollason (January 2002). "Computer shogi". Artificial Intelligence. 134 (1–2): 121–144. doi: 10.1016/S0004-3702(01)00157-6 .
  45. ↑ H. Adachi; H. Kamekawa; S. Iwata (1987). "Shogi on n × n board is complete in exponential time". Trans. IEICE. J70-D: 1843–1852.
  46. ↑ F.C. Schadd (2009). Monte-Carlo Search Techniques in the Modern Board Game Thurn and Taxis (PDF) (Thesis). Maastricht University. Archived from the original (PDF) on 2021-01-14.
  47. ↑ John Tromp; Gunnar Farnebäck (2007). "Combinatorics of Go". This paper derives the bounds 48<log(log(N))<171 on the number of possible games N.
  48. ↑ John Tromp (2016). "Number of legal Go positions".
  49. ↑ J. M. Robson (1983). "The complexity of Go". Information Processing; Proceedings of IFIP Congress. pp. 413–417.
  50. ↑ Christ-Jan Cox (2006). "Analysis and Implementation of the Game Arimaa" (PDF).
  51. ↑ David Jian Wu (2011). "Move Ranking and Evaluation in the Game of Arimaa" (PDF).
  52. ↑ Brian Haskin (2006). "A Look at the Arimaa Branching Factor".
  53. ↑ A.F.C. Arts (2010). Competitive Play in Stratego (PDF) (Thesis). Maastricht.
  54. ↑ CDA Evans and Joel David Hamkins (2014). "Transfinite game values in infinite chess". arXiv: 1302.4377 [math.LO].
  55. ↑ Stefan Reisch, Joel David Hamkins, and Phillipp Schlicht (2012). "The mate-in-n problem of infinite chess is decidable". Conference on Computability in Europe: 78–88. arXiv: 1201.5597 .{{cite journal}}: CS1 maint: multiple names: authors list (link)
  56. ↑ Alex Churchill, Stella Biderman, and Austin Herrick (2020). "Magic: the Gathering is Turing Complete". arXiv: 1904.09828 [cs.AI].{{cite arXiv}}: CS1 maint: multiple names: authors list (link)
  57. ↑ Stella Biderman (2020). "Magic: the Gathering is as Hard as Arithmetic". arXiv: 2003.05119 [cs.AI].
  58. ↑ Lokshtanov, Daniel; Subercaseaux, Bernardo (May 14, 2022). "Wordle is NP-hard". arXiv: 2203.16713 [cs.CC].

See also

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.