In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. The determinant of a matrix A is commonly denoted det(A), det A, or |A|. Its value characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants.
In mathematics, a product is the result of multiplication, or an expression that identifies objects to be multiplied, called factors. For example, 21 is the product of 3 and 7, and is the product of and . When one factor is an integer, the product is called a multiple.
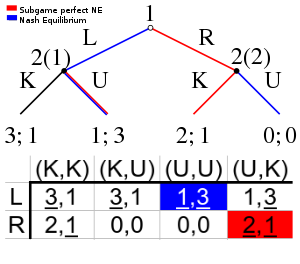
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equilibrium strategies of the other players, and no one has anything to gain by changing only one's own strategy. The principle of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to competing firms choosing outputs.

In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally,
In mathematics, a complex square matrix A is normal if it commutes with its conjugate transpose A*:

In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix A by producing another matrix, often denoted by AT.
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal matrix is , while an example of a 3×3 diagonal matrix is. An identity matrix of any size, or any multiple of it is a diagonal matrix called scalar matrix, for example, . In geometry, a diagonal matrix may be used as a scaling matrix, since matrix multiplication with it results in changing scale (size) and possibly also shape; only a scalar matrix results in uniform change in scale.
In mathematics, a triangular matrix is a special kind of square matrix. A square matrix is called lower triangular if all the entries above the main diagonal are zero. Similarly, a square matrix is called upper triangular if all the entries below the main diagonal are zero.
In statistics, the matrix normal distribution or matrix Gaussian distribution is a probability distribution that is a generalization of the multivariate normal distribution to matrix-valued random variables.
In linear algebra, linear transformations can be represented by matrices. If is a linear transformation mapping to and is a column vector with entries, then

In mathematics, an ordered basis of a vector space of finite dimension n allows representing uniquely any element of the vector space by a coordinate vector, which is a sequence of n scalars called coordinates. If two different bases are considered, the coordinate vector that represents a vector v on one basis is, in general, different from the coordinate vector that represents v on the other basis. A change of basis consists of converting every assertion expressed in terms of coordinates relative to one basis into an assertion expressed in terms of coordinates relative to the other basis.
In game theory, an extensive-form game is a specification of a game allowing for the explicit representation of a number of key aspects, like the sequencing of players' possible moves, their choices at every decision point, the information each player has about the other player's moves when they make a decision, and their payoffs for all possible game outcomes. Extensive-form games also allow for the representation of incomplete information in the form of chance events modeled as "moves by nature". Extensive-form representations differ from normal-form in that they provide a more complete description of the game in question, whereas normal-form simply boils down the game into a payoff matrix.
In game theory, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. Symmetry can come in different varieties. Ordinally symmetric games are games that are symmetric with respect to the ordinal structure of the payoffs. A game is quantitatively symmetric if and only if it is symmetric with respect to the exact payoffs. A partnership game is a symmetric game where both players receive identical payoffs for any strategy set. That is, the payoff for playing strategy a against strategy b receives the same payoff as playing strategy b against strategy a.
In linear algebra, eigendecomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. When the matrix being factorized is a normal or real symmetric matrix, the decomposition is called "spectral decomposition", derived from the spectral theorem.

In mathematics, trace diagrams are a graphical means of performing computations in linear and multilinear algebra. They can be represented as graphs in which some edges are labeled by matrices. The simplest trace diagrams represent the trace and determinant of a matrix. Several results in linear algebra, such as Cramer's Rule and the Cayley–Hamilton theorem, have simple diagrammatic proofs. They are closely related to Penrose's graphical notation.
A continuous game is a mathematical concept, used in game theory, that generalizes the idea of an ordinary game like tic-tac-toe or checkers (draughts). In other words, it extends the notion of a discrete game, where the players choose from a finite set of pure strategies. The continuous game concepts allows games to include more general sets of pure strategies, which may be uncountably infinite.
In mathematics, and in particular the study of game theory, a function is graph continuous if it exhibits the following properties. The concept was originally defined by Partha Dasgupta and Eric Maskin in 1986 and is a version of continuity that finds application in the study of continuous games.
In game theory, the common ways to describe a game are the normal form and the extensive form. The graphical form is an alternate compact representation of a game using the interaction among participants.
The Berge equilibrium is a game theory solution concept named after the mathematician Claude Berge. It is similar to the standard Nash equilibrium, except that it aims to capture a type of altruism rather than purely non-cooperative play. Whereas a Nash equilibrium is a situation in which each player of a strategic game ensures that they personally will receive the highest payoff given other players' strategies, in a Berge equilibrium every player ensures that all other players will receive the highest payoff possible. Although Berge introduced the intuition for this equilibrium notion in 1957, it was only formally defined by Vladislav Iosifovich Zhukovskii in 1985, and it was not in widespread use until half a century after Berge originally developed it.
In game theory, a satisfaction equilibrium is a solution concept for a class of non-cooperative games, namely games in satisfaction form. Games in satisfaction form model situations in which players aim at satisfying a given individual constraint, e.g., a performance metric must be smaller or bigger than a given threshold. When a player satisfies its own constraint, the player is said to be satisfied. A satisfaction equilibrium, if it exists, arises when all players in the game are satisfied.