First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded.
A Bayesian network is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to information science to computation (scheduling).
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning.

In probability theory, conditional independence describes situations wherein an observation is irrelevant or redundant when evaluating the certainty of a hypothesis. Conditional independence is usually formulated in terms of conditional probability, as a special case where the probability of the hypothesis given the uninformative observation is equal to the probability without. If is the hypothesis, and and are observations, conditional independence can be stated as an equality:
The Markov condition, sometimes called the Markov assumption, is an assumption made in Bayesian probability theory, that every node in a Bayesian network is conditionally independent of its nondescendants, given its parents. Stated loosely, it is assumed that a node has no bearing on nodes which do not descend from it. In a DAG, this local Markov condition is equivalent to the global Markov condition, which states that d-separations in the graph also correspond to conditional independence relations. This also means that a node is conditionally independent of the entire network, given its Markov blanket.
An influence diagram (ID) is a compact graphical and mathematical representation of a decision situation. It is a generalization of a Bayesian network, in which not only probabilistic inference problems but also decision making problems can be modeled and solved.
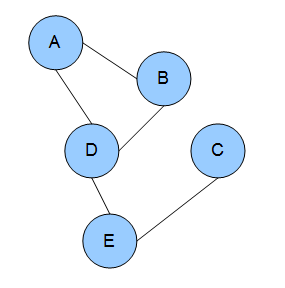
In the domain of physics and probability, a Markov random field (MRF), Markov network or undirected graphical model is a set of random variables having a Markov property described by an undirected graph. In other words, a random field is said to be a Markov random field if it satisfies Markov properties. The concept originates from the Sherrington–Kirkpatrick model.
In statistics, econometrics, epidemiology and related disciplines, the method of instrumental variables (IV) is used to estimate causal relationships when controlled experiments are not feasible or when a treatment is not successfully delivered to every unit in a randomized experiment. Intuitively, IVs are used when an explanatory variable of interest is correlated with the error term (endogenous), in which case ordinary least squares and ANOVA give biased results. A valid instrument induces changes in the explanatory variable but has no independent effect on the dependent variable and is not correlated with the error term, allowing a researcher to uncover the causal effect of the explanatory variable on the dependent variable.
In formal ontology, a branch of metaphysics, and in ontological computer science, mereotopology is a first-order theory, embodying mereological and topological concepts, of the relations among wholes, parts, parts of parts, and the boundaries between parts.
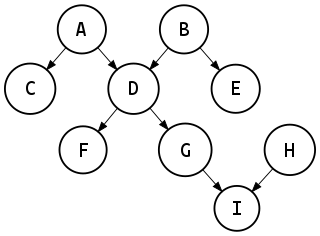
In mathematics, and more specifically in graph theory, a polytree is a directed acyclic graph whose underlying undirected graph is a tree. In other words, if we replace its directed edges with undirected edges, we obtain an undirected graph that is both connected and acyclic.
In the foundations of mathematics, Morse–Kelley set theory (MK), Kelley–Morse set theory (KM), Morse–Tarski set theory (MT), Quine–Morse set theory (QM) or the system of Quine and Morse is a first-order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory (NBG). While von Neumann–Bernays–Gödel set theory restricts the bound variables in the schematic formula appearing in the axiom schema of Class Comprehension to range over sets alone, Morse–Kelley set theory allows these bound variables to range over proper classes as well as sets, as first suggested by Quine in 1940 for his system ML.
Conditional random fields (CRFs) are a class of statistical modeling methods often applied in pattern recognition and machine learning and used for structured prediction. Whereas a classifier predicts a label for a single sample without considering "neighbouring" samples, a CRF can take context into account. To do so, the predictions are modelled as a graphical model, which represents the presence of dependencies between the predictions. What kind of graph is used depends on the application. For example, in natural language processing, "linear chain" CRFs are popular, for which each prediction is dependent only on its immediate neighbours. In image processing, the graph typically connects locations to nearby and/or similar locations to enforce that they receive similar predictions.

In graph theory, a moral graph is used to find the equivalent undirected form of a directed acyclic graph. It is a key step of the junction tree algorithm, used in belief propagation on graphical models.
General set theory (GST) is George Boolos's (1998) name for a fragment of the axiomatic set theory Z. GST is sufficient for all mathematics not requiring infinite sets, and is the weakest known set theory whose theorems include the Peano axioms.
Discriminative models, also referred to as conditional models, are a class of logistical models used for classification or regression. They distinguish decision boundaries through observed data, such as pass/fail, win/lose, alive/dead or healthy/sick.
Variable elimination (VE) is a simple and general exact inference algorithm in probabilistic graphical models, such as Bayesian networks and Markov random fields. It can be used for inference of maximum a posteriori (MAP) state or estimation of conditional or marginal distributions over a subset of variables. The algorithm has exponential time complexity, but could be efficient in practice for low-treewidth graphs, if the proper elimination order is used.
In statistics, econometrics, epidemiology, genetics and related disciplines, causal graphs are probabilistic graphical models used to encode assumptions about the data-generating process.
Dependency networks (DNs) are graphical models, similar to Markov networks, wherein each vertex (node) corresponds to a random variable and each edge captures dependencies among variables. Unlike Bayesian networks, DNs may contain cycles. Each node is associated to a conditional probability table, which determines the realization of the random variable given its parents.


















