Halin graph

Last updated

A Halin graph Halin graph.svg
A Halin graph

In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross (this is called a planar embedding), and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it. [1]

Contents

Halin graphs are named after German mathematician Rudolf Halin, who studied them in 1971. [2] The cubic Halin graphs – the ones in which each vertex touches exactly three edges – had already been studied over a century earlier by Kirkman. [3] Halin graphs are polyhedral graphs, meaning that every Halin graph can be used to form the vertices and edges of a convex polyhedron, and the polyhedra formed from them have been called roofless polyhedra or domes.

Every Halin graph has a Hamiltonian cycle through all its vertices, as well as cycles of almost all lengths up to the number of vertices of the graph. Halin graphs can be recognized in linear time. Because Halin graphs have low treewidth, many computational problems that are hard on other kinds of planar graphs, such as finding Hamiltonian cycles, can be solved quickly on Halin graphs.

A triangular prism, constructed as a Halin graph from a six-vertex tree Triangular prism as halin graph.svg
A triangular prism, constructed as a Halin graph from a six-vertex tree

Examples

Wheel graphs Wheel graphs.svg
Wheel graphs

A star is a tree with exactly one internal vertex. Applying the Halin graph construction to a star produces a wheel graph, the graph of the (edges of) a pyramid. [4] The graph of a triangular prism is also a Halin graph: it can be drawn so that one of its rectangular faces is the exterior cycle, and the remaining edges form a tree with four leaves, two interior vertices, and five edges. [5]

The Frucht graph, one of the five smallest cubic graphs with no nontrivial graph automorphisms, [6] is also a Halin graph. [7]

Properties

Every Halin graph is 3-connected, meaning that it is not possible to delete two vertices from it and disconnect the remaining vertices. It is edge-minimal 3-connected, meaning that if any one of its edges is removed, the remaining graph will no longer be 3-connected. [1] By Steinitz's theorem, as a 3-connected planar graph, it can be represented as the set of vertices and edges of a convex polyhedron; that is, it is a polyhedral graph. The polyhedron that realizes the graph can be chosen so that the face containing all of the tree leaves is horizontal, and all of the other faces lie above it, with equal slopes. [8] As with every polyhedral graph, Halin graphs have a unique planar embedding, up to the choice of which of its faces is to be the outer face. [1]

Every Halin graph is a Hamiltonian graph, and every edge of the graph belongs to a Hamiltonian cycle. Moreover, any Halin graph remains Hamiltonian after the deletion of any vertex. [9] Because every tree without vertices of degree 2 contains two leaves that share the same parent, every Halin graph contains a triangle. In particular, it is not possible for a Halin graph to be a triangle-free graph nor a bipartite graph. [10]

A Halin graph without any 8-cycles. A similar construction allows any single even cycle length to be avoided. Halin no 8-cycle.svg
A Halin graph without any 8-cycles. A similar construction allows any single even cycle length to be avoided.

More strongly, every Halin graph is almost pancyclic, in the sense that it has cycles of all lengths from 3 to n with the possible exception of a single even length. Moreover, any Halin graph remains almost pancyclic if a single edge is contracted, and every Halin graph without interior vertices of degree three is pancyclic. [12]

The incidence chromatic number of a Halin graph G with maximum degree Δ(G) greater than four is Δ(G) + 1. [13] This is the number of colors needed to color all pairs (v,e) where v is a vertex of the graph, and e is an edge incident to v, obeying certain constraints on the coloring. Pairs that share a vertex or that share an edge are not allowed to have the same color. In addition, a pair (v,e) cannot have the same color as another pair that uses the other endpoint of e. For Halin graphs with Δ(G) = 3 or 4, the incidence chromatic number may be as large as 5 or 6 respectively. [14]

Computational complexity

It is possible to test whether a given n-vertex graph is a Halin graph in linear time, by finding a planar embedding of the graph (if one exists), and then testing whether there exists a face that has at least n/2 + 1 vertices, all of degree three. If so, there can be at most four such faces, and it is possible to check in linear time for each of them whether the rest of the graph forms a tree with the vertices of this face as its leaves. On the other hand, if no such face exists, then the graph is not Halin. [15] Alternatively, a graph with n vertices and m edges is Halin if and only if it is planar, 3-connected, and has a face whose number of vertices equals the circuit rank m−n + 1 of the graph, all of which can be checked in linear time. [16] Other methods for recognizing Halin graphs in linear time include the application of Courcelle's theorem, or a method based on graph rewriting, neither of which rely on knowing the planar embedding of the graph. [17]

Every Halin graph has treewidth = 3. [18] Therefore, many graph optimization problems that are NP-complete for arbitrary planar graphs, such as finding a maximum independent set, may be solved in linear time on Halin graphs using dynamic programming [19] or Courcelle's theorem, or in some cases (such as the construction of Hamiltonian cycles) by direct algorithms. [17] However, it is NP-complete to find the largest Halin subgraph of a given graph, to test whether there exists a Halin subgraph that includes all vertices of a given graph, or to test whether a given graph is a subgraph of a larger Halin graph. [20]

History

In 1971, Halin introduced the Halin graphs as a class of minimally 3-vertex-connected graphs: for every edge in the graph, the removal of that edge reduces the connectivity of the graph. [2] These graphs gained significance with the discovery that many algorithmic problems that were computationally infeasible for arbitrary planar graphs could be solved efficiently on them. [9] [16] This fact was later explained to be a consequence of their low treewidth, and of algorithmic meta-theorems like Courcelle's theorem that provide efficient solutions to these problems on any graph of low treewidth. [18] [19]

Prior to Halin's work on these graphs, graph enumeration problems concerning the cubic (or 3-regular) Halin graphs were studied in 1856 by Thomas Kirkman [3] and in 1965 by Hans Rademacher. Rademacher calls these graphs based polyhedra. He defines them as the cubic polyhedral graphs with f faces in which one of the faces has f− 1 sides. [21] The graphs that fit this definition are exactly the cubic Halin graphs. [22]

Inspired by the fact that both Halin graphs and 4-vertex-connected planar graphs contain Hamiltonian cycles, Lovász & Plummer (1974) conjectured that every 4-vertex-connected planar graph contains a spanning Halin subgraph; here "spanning" means that the subgraph includes all vertices of the larger graph. The Lovász–Plummer conjecture remained open until 2015, when a construction for infinitely many counterexamples was published. [23]

The Halin graphs are sometimes also called skirted trees [11] or roofless polyhedra. [9] However, these names are ambiguous. Some authors use the name "skirted trees" to refer to planar graphs formed from trees by connecting the leaves into a cycle, but without requiring that the internal vertices of the tree have degree three or more. [24] And like "based polyhedra", the "roofless polyhedra" name may also refer to the cubic Halin graphs. [22] The convex polyhedra whose graphs are Halin graphs have also been called domes. [25]

Related Research Articles

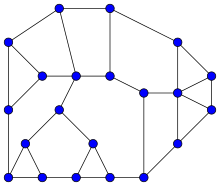
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In mathematics, Tait's conjecture states that "Every 3-connected planar cubic graph has a Hamiltonian cycle through all its vertices". It was proposed by P. G. Tait (1884) and disproved by W. T. Tutte (1946), who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by Holton & McKay (1988). The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron, which forms a bipartite graph with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian.

<span class="mw-page-title-main">Hamiltonian path</span> Path in a graph that visits each vertex exactly once

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. Determining whether such paths and cycles exist in graphs are NP-complete.

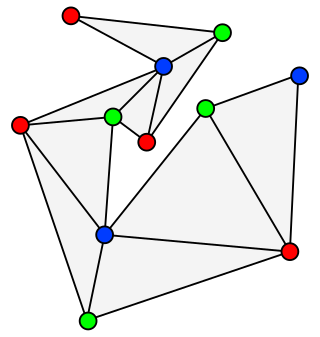
<span class="mw-page-title-main">Outerplanar graph</span> Non-crossing graph with vertices on outer face

In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

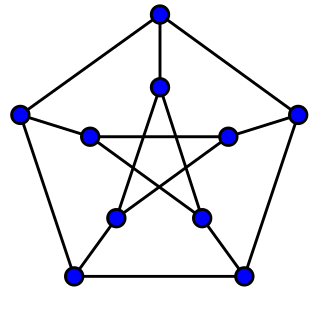
<span class="mw-page-title-main">Snark (graph theory)</span> 3-regular graph with no 3-edge-coloring

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

<span class="mw-page-title-main">Dual graph</span> Graph representing faces of another graph

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.

<span class="mw-page-title-main">Factor-critical graph</span> Graph of n vertices with a perfect matching for every subgraph of n-1 vertices

In graph theory, a mathematical discipline, a factor-critical graph is a graph with n vertices in which every subgraph of n − 1 vertices has a perfect matching.

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

<span class="mw-page-title-main">Grinberg's theorem</span> On Hamiltonian cycles in planar graphs

In graph theory, Grinberg's theorem is a necessary condition for a planar graph to contain a Hamiltonian cycle, based on the lengths of its face cycles. If a graph does not meet this condition, it is not Hamiltonian. The result has been widely used to prove that certain planar graphs constructed to have additional properties are not Hamiltonian; for instance it can prove non-Hamiltonicity of some counterexamples to Tait's conjecture that cubic polyhedral graphs are Hamiltonian.

<span class="mw-page-title-main">Hamiltonian decomposition</span>

In graph theory, a branch of mathematics, a Hamiltonian decomposition of a given graph is a partition of the edges of the graph into Hamiltonian cycles. Hamiltonian decompositions have been studied both for undirected graphs and for directed graphs. In the undirected case a Hamiltonian decomposition can also be described as a 2-factorization of the graph such that each factor is connected.

<span class="mw-page-title-main">Polyhedral graph</span> Graph made from vertices and edges of a convex polyhedron

In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs.

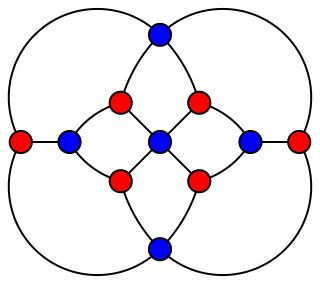
<span class="mw-page-title-main">Herschel graph</span> Bipartite non-Hamiltonian polyhedral graph

In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges. It is a polyhedral graph, and is the smallest polyhedral graph that does not have a Hamiltonian cycle, a cycle passing through all its vertices. It is named after British astronomer Alexander Stewart Herschel, because of Herschel's studies of Hamiltonian cycles in polyhedral graphs.

Barnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W. Barnette, a professor emeritus at the University of California, Davis; it states that every bipartite polyhedral graph with three edges per vertex has a Hamiltonian cycle.

<span class="mw-page-title-main">Pancyclic graph</span>

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.

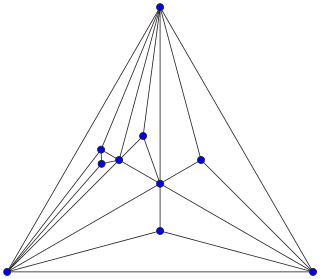
<span class="mw-page-title-main">Apollonian network</span> Graph formed by subdivision of triangles

In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

In graph theory, a branch of mathematics, Halin's grid theorem states that the infinite graphs with thick ends are exactly the graphs containing subdivisions of the hexagonal tiling of the plane. It was published by Rudolf Halin (1965), and is a precursor to the work of Robertson and Seymour linking treewidth to large grid minors, which became an important component of the algorithmic theory of bidimensionality.

In graph theory and graph drawing, a subhamiltonian graph is a subgraph of a planar Hamiltonian graph.

In the mathematical field of graph theory, a prism graph is a graph that has one of the prisms as its skeleton.

<span class="mw-page-title-main">Barnette–Bosák–Lederberg graph</span> Non-Hamiltonian simple polyhedron

In the mathematical field of graph theory, the Barnette–Bosák–Lederberg graph is a cubic polyhedral graph with no Hamiltonian cycle, the smallest such graph possible. It was discovered in the mid-1960s by Joshua Lederberg, David Barnette, and Juraj Bosák, after whom it is named. It has 38 vertices and 69 edges.

References

  1. 1 2 3 Encyclopaedia of Mathematics, first Supplementary volume, 1988, ISBN   0-7923-4709-9, p. 281, article "Halin Graph", and references therein.
  2. 1 2 Halin, R. (1971), "Studies on minimally n-connected graphs", Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), London: Academic Press, pp. 129–136, MR   0278980 .
  3. 1 2 Kirkman, Th. P. (1856), "On the enumeration of x-edra having triedral summits and an (x− 1)-gonal base", Philosophical Transactions of the Royal Society of London, 146: 399–411, doi: 10.1098/rstl.1856.0018 , JSTOR   108592 .
  4. ↑ Cornuéjols, Naddef & Pulleyblank (1983): "If T is a star, i.e., a single node v joined to n other nodes, then H is called a wheel and is the simplest type of Halin graph."
  5. ↑ See Sysło & Proskurowski (1983), Prop. 4.3, p. 254, which identifies the triangular prism as the unique graph with exactly three cycles that can be the outer cycle of a realization as a Halin graph.
  6. ↑ Bussemaker, F. C.; Cobeljic, S.; Cvetkovic, D. M.; Seidel, J. J. (1976), "Computer investigation of cubic graphs", Eindhoven University of Technology Research Portal, EUT report, Dept. of Mathematics and Computing Science, Eindhoven University of Technology, 76-WSK-01
  7. ↑ Weisstein, Eric W., "Halin Graph", MathWorld
  8. ↑ Aichholzer, Oswin; Cheng, Howard; Devadoss, Satyan L.; Hackl, Thomas; Huber, Stefan; Li, Brian; Risteski, Andrej (2012), "What makes a tree a straight skeleton?" (PDF), Proceedings of the 24th Canadian Conference on Computational Geometry (CCCG'12)
  9. 1 2 3 Cornuéjols, G.; Naddef, D.; Pulleyblank, W. R. (1983), "Halin graphs and the travelling salesman problem", Mathematical Programming , 26 (3): 287–294, doi:10.1007/BF02591867, S2CID   26278382 .
  10. ↑ See the proof of Theorem 10 in Wang, Weifan; Bu, Yuehua; Montassier, Mickaël; Raspaud, André (2012), "On backbone coloring of graphs", Journal of Combinatorial Optimization, 23 (1): 79–93, doi:10.1007/s10878-010-9342-6, MR   2875236, S2CID   26975523 : "Since G contains a 3-cycle consisting of one inner vertex and two outer vertices, G is not a bipartite graph."
  11. 1 2 Malkevitch, Joseph (1978), "Cycle lengths in polytopal graphs", Theory and Applications of Graphs (Proc. Internat. Conf., Western Mich. Univ., Kalamazoo, Mich., 1976), Lecture Notes in Mathematics, vol. 642, Berlin: Springer, pp. 364–370, doi:10.1007/BFb0070393, ISBN   978-3-540-08666-6, MR   0491287
  12. ↑ Skowrońska, Mirosława (1985), "The pancyclicity of Halin graphs and their exterior contractions", in Alspach, Brian R.; Godsil, Christopher D. (eds.), Cycles in Graphs, Annals of Discrete Mathematics, vol. 27, Elsevier Science Publishers B.V., pp. 179–194.
  13. ↑ Wang, Shu-Dong; Chen, Dong-Ling; Pang, Shan-Chen (2002), "The incidence coloring number of Halin graphs and outerplanar graphs", Discrete Mathematics , 256 (1–2): 397–405, doi:10.1016/S0012-365X(01)00302-8, MR   1927561 .
  14. ↑ Shiu, W. C.; Sun, P. K. (2008), "Invalid proofs on incidence coloring", Discrete Mathematics , 308 (24): 6575–6580, doi: 10.1016/j.disc.2007.11.030 , MR   2466963 .
  15. ↑ Fomin, Fedor V.; Thilikos, Dimitrios M. (2006), "A 3-approximation for the pathwidth of Halin graphs", Journal of Discrete Algorithms, 4 (4): 499–510, doi: 10.1016/j.jda.2005.06.004 , MR   2577677 .
  16. 1 2 Sysło, Maciej M.; Proskurowski, Andrzej (1983), "On Halin graphs", Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–13, 1981, Lecture Notes in Mathematics, vol. 1018, Springer-Verlag, pp. 248–256, doi:10.1007/BFb0071635 .
  17. 1 2 Eppstein, David (2016), "Simple recognition of Halin graphs and their generalizations", Journal of Graph Algorithms and Applications , 20 (2): 323–346, arXiv: 1502.05334 , doi:10.7155/jgaa.00395, S2CID   9525753 .
  18. 1 2 Bodlaender, Hans (1988), Planar graphs with bounded treewidth (PDF), Technical Report RUU-CS-88-14, Department of Computer Science, Utrecht University, archived from the original (PDF) on 2004-07-28.
  19. 1 2 Bodlaender, Hans (1988), "Dynamic programming on graphs with bounded treewidth", Proceedings of the 15th International Colloquium on Automata, Languages and Programming, Lecture Notes in Computer Science, vol. 317, Springer-Verlag, pp. 105–118, doi:10.1007/3-540-19488-6_110, hdl: 1874/16258 , ISBN   978-3540194880 .
  20. ↑ Horton, S. B.; Parker, R. Gary (1995), "On Halin subgraphs and supergraphs", Discrete Applied Mathematics , 56 (1): 19–35, doi: 10.1016/0166-218X(93)E0131-H , MR   1311302 .
  21. ↑ Rademacher, Hans (1965), "On the number of certain types of polyhedra", Illinois Journal of Mathematics, 9 (3): 361–380, doi: 10.1215/ijm/1256068140 , MR   0179682 .
  22. 1 2 Lovász, L.; Plummer, M. D. (1974), "On a family of planar bicritical graphs", Combinatorics (Proc. British Combinatorial Conf., Univ. Coll. Wales, Aberystwyth, 1973), London: Cambridge Univ. Press, pp. 103–107. London Math. Soc. Lecture Note Ser., No. 13, MR   0351915 .
  23. ↑ Chen, Guantao; Enomoto, Hikoe; Ozeki, Kenta; Tsuchiya, Shoichi (2015), "Plane triangulations without a spanning Halin subgraph: counterexamples to the Lovász-Plummer conjecture on Halin graphs", SIAM Journal on Discrete Mathematics , 29 (3): 1423–1426, doi:10.1137/140971610, MR   3376776 .
  24. ↑ Skowrońska, M.; Sysło, M. M. (1987), "Hamiltonian cycles in skirted trees", Proceedings of the International Conference on Combinatorial Analysis and its Applications (Pokrzywna, 1985), Zastos. Mat., 19 (3–4): 599–610 (1988), MR   0951375
  25. ↑ Demaine, Erik D.; Demaine, Martin L.; Uehara, Ryuhei (2013), "Zipper unfolding of domes and prismoids", Proceedings of the 25th Canadian Conference on Computational Geometry (CCCG 2013), Waterloo, Ontario, Canada, August 8–10, 2013, pp. 43–48.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.