In set theory, a hereditary set (or pure set) is a set whose elements are all hereditary sets. That is, all elements of the set are themselves sets, as are all elements of the elements, and so on.
For example, it is vacuously true that the empty set is a hereditary set, and thus the set containing only the empty set is a hereditary set. Similarly, a set that contains two elements: the empty set and the set that contains only the empty set, is a hereditary set.
In formulations of set theory that are intended to be interpreted in the von Neumann universe or to express the content of Zermelo–Fraenkel set theory, all sets are hereditary, because the only sort of object that is even a candidate to be an element of a set is another set. Thus the notion of hereditary set is interesting only in a context in which there may be urelements.
The inductive definition of hereditary sets presupposes that set membership is well-founded (i.e., the axiom of regularity), otherwise the recurrence may not have a unique solution. However, it can be restated non-inductively as follows: a set is hereditary if and only if its transitive closure contains only sets. In this way the concept of hereditary sets can also be extended to non-well-founded set theories in which sets can be members of themselves. For example, a set that contains only itself is a hereditary set.
In mathematics, the axiom of regularity is an axiom of Zermelo–Fraenkel set theory that states that every non-empty set A contains an element that is disjoint from A. In first-order logic, the axiom reads:
In mathematics, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories ensure that the empty set exists by including an axiom of empty set, while in other theories, its existence can be deduced. Many possible properties of sets are vacuously true for the empty set.
In mathematics, particularly set theory, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting. For example,
In mathematics, a filter or order filter is a special subset of a partially ordered set (poset). Filters appear in order and lattice theory, but can also be found in topology, from which they originate. The dual notion of a filter is an order ideal.
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded.
In mathematics, the well-ordering principle states that every non-empty set of positive integers contains a least element. In other words, the set of positive integers is well-ordered by its "natural" or "magnitude" order in which precedes if and only if is either or the sum of and some positive integer.
In mathematics, an empty product, or nullary product or vacuous product, is the result of multiplying no factors. It is by convention equal to the multiplicative identity, just as the empty sum—the result of adding no numbers—is by convention zero, or the additive identity. When numbers are implied, the empty product becomes one.
In axiomatic set theory and the branches of mathematics and philosophy that use it, the axiom of infinity is one of the axioms of Zermelo–Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural numbers. It was first published by Ernst Zermelo as part of his set theory in 1908.
In mathematics, and particularly in set theory, category theory, type theory, and the foundations of mathematics, a universe is a collection that contains all the entities one wishes to consider in a given situation.
In mathematics and set theory, hereditarily finite sets are defined as finite sets whose elements are all hereditarily finite sets. In other words, the set itself is finite, and all of its elements are finite sets, recursively all the way down to the empty set.
In mathematics, in set theory, the constructible universe, denoted by L, is a particular class of sets that can be described entirely in terms of simpler sets. L is the union of the constructible hierarchyLα . It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". In this paper, he proved that the constructible universe is an inner model of ZF set theory, and also that the axiom of choice and the generalized continuum hypothesis are true in the constructible universe. This shows that both propositions are consistent with the basic axioms of set theory, if ZF itself is consistent. Since many other theorems only hold in systems in which one or both of the propositions is true, their consistency is an important result.
In general topology, a branch of mathematics, a non-empty family A of subsets of a set is said to have the finite intersection property (FIP) if the intersection over any finite subcollection of is non-empty. It has the strong finite intersection property (SFIP) if the intersection over any finite subcollection of is infinite.
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by V, is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930.
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.
In the mathematical field of topology, the inductive dimension of a topological space X is either of two values, the small inductive dimension ind(X) or the large inductive dimension Ind(X). These are based on the observation that, in n-dimensional Euclidean space Rn, (n − 1)-dimensional spheres have dimension n − 1. Therefore it should be possible to define the dimension of a space inductively in terms of the dimensions of the boundaries of suitable open sets.
In measure theory, Carathéodory's extension theorem states that any pre-measure defined on a given ring R of subsets of a given set Ω can be extended to a measure on the σ-algebra generated by R, and this extension is unique if the pre-measure is σ-finite. Consequently, any pre-measure on a ring containing all intervals of real numbers can be extended to the Borel algebra of the set of real numbers. This is an extremely powerful result of measure theory, and leads, for example, to the Lebesgue measure.
General set theory (GST) is George Boolos's (1998) name for a fragment of the axiomatic set theory Z. GST is sufficient for all mathematics not requiring infinite sets, and is the weakest known set theory whose theorems include the Peano axioms.
In mathematics, a hereditary property is a property of an object that is inherited by all of its subobjects, where the meaning of subobject depends on the context. These properties are particularly considered in topology and graph theory, but also in set theory.
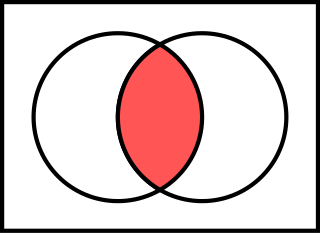
In mathematics, the intersection of two sets and denoted by is the set containing all elements of that also belong to or equivalently, all elements of that also belong to
In the mathematical field of set theory, an ultrafilter is a maximal proper filter: it is a filter on a given non-empty set which is a certain type of non-empty family of subsets of that is not equal to the power set of and that is also "maximal" in that there does not exist any other proper filter on that contains it as a proper subset. Said differently, a proper filter is called an ultrafilter if there exists exactly one proper filter that contains it as a subset, that proper filter (necessarily) being itself.
| General | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Theorems (list) & Paradoxes | |||||||||
| Logics |
| ||||||||
| Set theory |
| ||||||||
| Syntax & Language |
| ||||||||
| Proof theory | |||||||||
| Model theory | |||||||||
| Computability theory | |||||||||
| Related | |||||||||
