Hilbert's axioms

Last updated

Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie [1] [2] [3] [4] (tr. The Foundations of Geometry) as the foundation for a modern treatment of Euclidean geometry. Other well-known modern axiomatizations of Euclidean geometry are those of Alfred Tarski and of George Birkhoff.

Contents

The axioms

Hilbert's axiom system is constructed with six primitive notions: three primitive terms: [5]

and three primitive relations: [6]

Line segments, angles, and triangles may each be defined in terms of points and straight lines, using the relations of betweenness and containment. All points, straight lines, and planes in the following axioms are distinct unless otherwise stated.

I. Incidence

  1. For every two points A and B there exists a line a that contains them both. We write AB = a or BA = a. Instead of "contains", we may also employ other forms of expression; for example, we may say "A lies upon a", "A is a point of a", "a goes through A and through B", "a joins A to B", etc. If A lies upon a and at the same time upon another line b, we make use also of the expression: "The lines a and b have the point A in common", etc.
  2. For every two points there exists no more than one line that contains them both; consequently, if AB = a and AC = a, where B ≠ C, then also BC = a.
  3. There exist at least two points on a line. There exist at least three points that do not lie on the same line.
  4. For every three points A, B, C not situated on the same line there exists a plane α that contains all of them. For every plane there exists a point which lies on it. We write ABC = α. We employ also the expressions: "A, B, C lie in α"; "A, B, C are points of α", etc.
  5. For every three points A, B, C which do not lie in the same line, there exists no more than one plane that contains them all.
  6. If two points A, B of a line a lie in a plane α, then every point of a lies in α. In this case we say: "The line a lies in the plane α", etc.
  7. If two planes α, β have a point A in common, then they have at least a second point B in common.
  8. There exist at least four points not lying in a plane.

II. Order

  1. If a point B lies between points A and C, B is also between C and A, and there exists a line containing the distinct points A, B, C.
  2. If A and C are two points, then there exists at least one point B on the line AC such that C lies between A and B. [7]
  3. Of any three points situated on a line, there is no more than one which lies between the other two. [8]
  4. Pasch's Axiom: Let A, B, C be three points not lying in the same line and let a be a line lying in the plane ABC and not passing through any of the points A, B, C. Then, if the line a passes through a point of the segment AB, it will also pass through either a point of the segment BC or a point of the segment AC.

III. Congruence

  1. If A, B are two points on a line a, and if A′ is a point upon the same or another line a′, then, upon a given side of A′ on the straight line a′, we can always find a point B′ so that the segment AB is congruent to the segment A′B′. We indicate this relation by writing AB ≅ A′B′. Every segment is congruent to itself; that is, we always have AB ≅ AB.
    We can state the above axiom briefly by saying that every segment can be laid off upon a given side of a given point of a given straight line in at least one way.
  2. If a segment AB is congruent to the segment A′B′ and also to the segment A″B″, then the segment A′B′ is congruent to the segment A″B″; that is, if AB ≅ A′B′ and AB ≅ A″B″, then A′B′ ≅ A″B″.
  3. Let AB and BC be two segments of a line a which have no points in common aside from the point B, and, furthermore, let A′B′ and B′C′ be two segments of the same or of another line a′ having, likewise, no point other than B′ in common. Then, if AB ≅ A′B′ and BC ≅ B′C′, we have AC ≅ A′C′.
  4. Let an angle ∠ (h,k) be given in the plane α and let a line a′ be given in a plane α′. Suppose also that, in the plane α′, a definite side of the straight line a′ be assigned. Denote by h′ a ray of the straight line a′ emanating from a point O′ of this line. Then in the plane α′ there is one and only one ray k′ such that the angle ∠ (h, k), or ∠ (k, h), is congruent to the angle ∠ (h′, k′) and at the same time all interior points of the angle ∠ (h′, k′) lie upon the given side of a′. We express this relation by means of the notation ∠ (h, k) ≅ ∠ (h′, k′).
  5. If the angle ∠ (h, k) is congruent to the angle ∠ (h′, k′) and to the angle ∠ (h″, k″), then the angle ∠ (h′, k′) is congruent to the angle ∠ (h″, k″); that is to say, if ∠ (h, k) ≅ ∠ (h′, k′) and ∠ (h, k) ≅ ∠ (h″, k″), then ∠ (h′, k′) ≅ ∠ (h″, k″).
  6. If, in the two triangles ABC and A′B′C′ the congruences AB ≅ A′B′, AC ≅ A′C′, ∠BAC ≅ ∠B′A′C′ hold, then the congruence ∠ABC ≅ ∠A′B′C′ holds (and, by a change of notation, it follows that ∠ACB ≅ ∠A′C′B′ also holds).

IV. Parallels

  1. Euclid's Axiom: [9] Let a be any line and A a point not on it. Then there is at most one line in the plane, determined by a and A, that passes through A and does not intersect a.

V. Continuity

  1. Axiom of Archimedes: If AB and CD are any segments then there exists a number n such that n segments CD constructed contiguously from A, along the ray from A through B, will pass beyond the point B.
  2. Axiom of line completeness: An extension (An extended line from a line that already exists, usually used in geometry) of a set of points on a line with its order and congruence relations that would preserve the relations existing among the original elements as well as the fundamental properties of line order and congruence that follows from Axioms I-III and from V-1 is impossible.

Hilbert's discarded axiom

Hilbert (1899) included a 21st axiom that read as follows:

II.4. Any four points A, B, C, D of a line can always be labeled so that B shall lie between A and C and also between A and D, and, furthermore, that C shall lie between A and D and also between B and D.

This statement is also known as Pasch's theorem.

E.H. Moore and R.L. Moore independently proved that this axiom is redundant, and the former published this result in an article appearing in the Transactions of the American Mathematical Society in 1902. [10]

Before this, Pasch's axiom, now listed as II.4., was numbered II.5.

Editions and translations of Grundlagen der Geometrie

The original monograph, based on his own lectures, was organized and written by Hilbert for a memorial address given in 1899. This was quickly followed by a French translation, in which Hilbert added V.2, the Completeness Axiom. An English translation, authorized by Hilbert, was made by E.J. Townsend and copyrighted in 1902. This translation incorporated the changes made in the French translation and so is considered to be a translation of the 2nd edition. Hilbert continued to make changes in the text and several editions appeared in German. The 7th edition was the last to appear in Hilbert's lifetime. In the Preface of this edition Hilbert wrote:

"The present Seventh Edition of my book Foundations of Geometry brings considerable improvements and additions to the previous edition, partly from my subsequent lectures on this subject and partly from improvements made in the meantime by other writers. The main text of the book has been revised accordingly."

New editions followed the 7th, but the main text was essentially not revised. The modifications in these editions occur in the appendices and in supplements. The changes in the text were large when compared to the original and a new English translation was commissioned by Open Court Publishers, who had published the Townsend translation. So, the 2nd English Edition was translated by Leo Unger from the 10th German edition in 1971. This translation incorporates several revisions and enlargements of the later German editions by Paul Bernays.

The Unger translation differs from the Townsend translation with respect to the axioms in the following ways:

Axiom of completeness. To a system of points, straight lines, and planes, it is impossible to add other elements in such a manner that the system thus generalized shall form a new geometry obeying all of the five groups of axioms. In other words, the elements of geometry form a system which is not susceptible of extension, if we regard the five groups of axioms as valid.

The last two modifications are due to P. Bernays.

Other changes of note are:

Application

These axioms axiomatize Euclidean solid geometry. Removing five axioms mentioning "plane" in an essential way, namely I.4–8, and modifying III.4 and IV.1 to omit mention of planes, yields an axiomatization of Euclidean plane geometry.

Hilbert's axioms, unlike Tarski's axioms, do not constitute a first-order theory because the axioms V.1–2 cannot be expressed in first-order logic.

The value of Hilbert's Grundlagen was more methodological than substantive or pedagogical. Other major contributions to the axiomatics of geometry were those of Moritz Pasch, Mario Pieri, Oswald Veblen, Edward Vermilye Huntington, Gilbert Robinson, and Henry George Forder. The value of the Grundlagen is its pioneering approach to metamathematical questions, including the use of models to prove axioms independent; and the need to prove the consistency and completeness of an axiom system.

Mathematics in the twentieth century evolved into a network of axiomatic formal systems. This was, in considerable part, influenced by the example Hilbert set in the Grundlagen. A 2003 effort (Meikle and Fleuriot) to formalize the Grundlagen with a computer, though, found that some of Hilbert's proofs appear to rely on diagrams and geometric intuition, and as such revealed some potential ambiguities and omissions in his definitions. [11]

See also

Notes

  1. ↑ Sommer, Julius (1900). "Review: Grundlagen der Geometrie, Teubner, 1899" (PDF). Bull. Amer. Math. Soc. 6 (7): 287–299. doi: 10.1090/s0002-9904-1900-00719-1 .
  2. ↑ Poincaré, Henri (1903). "Poincaré's review of Hilbert's "Foundations of Geometry", translated by E. V. Huntington" (PDF). Bull. Amer. Math. Soc. 10: 1–23. doi: 10.1090/S0002-9904-1903-01061-1 .
  3. ↑ Schweitzer, Arthur Richard (1909). "Review: Grundlagen der Geometrie, Third edition, Teubner, 1909" (PDF). Bull. Amer. Math. Soc. 15 (10): 510–511. doi: 10.1090/s0002-9904-1909-01814-2 .
  4. ↑ Gronwall, T. H. (1919). "Review: Grundlagen der Geometrie, Fourth edition, Teubner, 1913" (PDF). Bull. Amer. Math. Soc. 20 (6): 325–326. doi: 10.1090/S0002-9904-1914-02492-9 .
  5. ↑ These axioms and their numbering are taken from the Unger translation (into English) of the 10th edition of Grundlagen der Geometrie.
  6. ↑ One could count this as six relations as specified below, but Hilbert did not do so.
  7. ↑ In the Townsend edition this statement differs in that it also includes the existence of at least one point D with C between A and D, which became a theorem in a later edition.
  8. ↑ The existence part ("there is at least one") is a theorem.
  9. ↑ This is Hilbert's terminology. This statement is more familiarly known as Playfair's axiom.
  10. ↑ Moore, E.H. (1902), "On the projective axioms of geometry" (PDF), Transactions of the American Mathematical Society, 3 (1): 142–158, doi: 10.2307/1986321 , JSTOR   1986321
  11. ↑ On page 334: "By formalizing the Grundlagen in Isabelle/Isar we showed that Hilbert's work glossed over subtle points of reasoning and relied heavily, in some cases, on diagrams which allowed implicit assumptions to be made. For this reason it can be argued that Hilbert interleaved his axioms with geometric intuition in order to prove many of his theorems."

Related Research Articles

<span class="mw-page-title-main">Euclidean geometry</span> Mathematical model of the physical space

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

<span class="mw-page-title-main">Euclidean space</span> Fundamental space of geometry

Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are called Euclidean n-spaces when one wants to specify their dimension. For n equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.

<span class="mw-page-title-main">Similarity (geometry)</span> Property of objects which are scaled or mirrored versions of each other

In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.

<span class="mw-page-title-main">Perpendicular</span> Relationship between two lines that meet at a right angle (90 degrees)

In elementary geometry, two geometric objects are perpendicular if their intersection forms right angles at the point of intersection called a foot. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. Perpendicular intersections can happen between two lines, between a line and a plane, and between two planes.

<span class="mw-page-title-main">Affine geometry</span> Euclidean geometry without distance and angles

In mathematics, affine geometry is what remains of Euclidean geometry when ignoring the metric notions of distance and angle.

In geometry, parallel lines are coplanar infinite straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. Parallel curves are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called skew lines. Line segments and Euclidean vectors are parallel if they have the same direction.

<span class="mw-page-title-main">Line (geometry)</span> Straight figure with zero width and depth

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.

In mathematics, Hilbert's fourth problem in the 1900 list of Hilbert's problems is a foundational question in geometry. In one statement derived from the original, it was to find — up to an isomorphism — all geometries that have an axiomatic system of the classical geometry, with those axioms of congruence that involve the concept of the angle dropped, and `triangle inequality', regarded as an axiom, added.

In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An incidence structure is what is obtained when all other concepts are removed and all that remains is the data about which points lie on which lines. Even with this severe limitation, theorems can be proved and interesting facts emerge concerning this structure. Such fundamental results remain valid when additional concepts are added to form a richer geometry. It sometimes happens that authors blur the distinction between a study and the objects of that study, so it is not surprising to find that some authors refer to incidence structures as incidence geometries.

Tarski's axioms, due to Alfred Tarski, are an axiom set for the substantial fragment of Euclidean geometry that is formulable in first-order logic with identity, and requiring no set theory. Other modern axiomizations of Euclidean geometry are Hilbert's axioms and Birkhoff's axioms.

<span class="mw-page-title-main">Karl Georg Christian von Staudt</span> German mathematician

Karl Georg Christian von Staudt was a German mathematician who used synthetic geometry to provide a foundation for arithmetic.

<span class="mw-page-title-main">Angle bisector theorem</span> Geometrical theorem relating the lengths of two segments that divide a triangle

In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

<span class="mw-page-title-main">Hjelmslev transformation</span>

In mathematics, the Hjelmslev transformation is an effective method for mapping an entire hyperbolic plane into a circle with a finite radius. The transformation was invented by Danish mathematician Johannes Hjelmslev. It utilizes Nikolai Ivanovich Lobachevsky's 23rd theorem from his work Geometrical Investigations on the Theory of Parallels.

In geometry, Pasch's axiom is a statement in plane geometry, used implicitly by Euclid, which cannot be derived from the postulates as Euclid gave them. Its essential role was discovered by Moritz Pasch in 1882.

<span class="mw-page-title-main">Hypercycle (geometry)</span> Type of curve in hyperbolic geometry

In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line.

Ordered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement. Ordered geometry is a fundamental geometry forming a common framework for affine, Euclidean, absolute, and hyperbolic geometry.

Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

<span class="mw-page-title-main">Playfair's axiom</span> Modern formulation of Euclids parallel postulate

In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid :

In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.

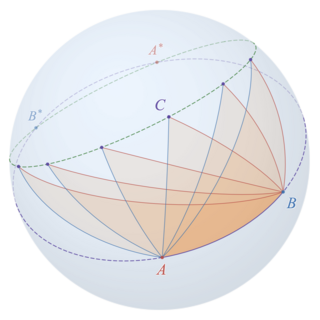
<span class="mw-page-title-main">Lexell's theorem</span> Characterizes spherical triangles with fixed base and area

In spherical geometry, Lexell's theorem holds that every spherical triangle with the same surface area on a fixed base has its apex on a small circle, called Lexell's circle or Lexell's locus, passing through each of the two points antipodal to the two base vertices.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.