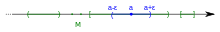In mathematics, a continuous function is a function such that a continuous variation of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as discontinuities. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is not continuous. Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity.
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.

In mathematics, an open set is a generalization of an open interval in the real line.
In topology, the closure of a subset S of points in a topological space consists of all points in S together with all limit points of S. The closure of S may equivalently be defined as the union of S and its boundary, and also as the intersection of all closed sets containing S. Intuitively, the closure can be thought of as all the points that are either in S or "very near" S. A point which is in the closure of S is a point of closure of S. The notion of closure is in many ways dual to the notion of interior.
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis. A topological vector space is a vector space that is also a topological space with the property that the vector space operations are also continuous functions. Such a topology is called a vector topology and every topological vector space has a uniform topological structure, allowing a notion of uniform convergence and completeness. Some authors also require that the space is a Hausdorff space. One of the most widely studied categories of TVSs are locally convex topological vector spaces. This article focuses on TVSs that are not necessarily locally convex. Banach spaces, Hilbert spaces and Sobolev spaces are other well-known examples of TVSs.
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points. In a complete metric space, a closed set is a set which is closed under the limit operation. This should not be confused with a closed manifold.
A subset of a topological space is called a regular open set if it is equal to the interior of its closure; expressed symbolically, if or, equivalently, if where and denote, respectively, the interior, closure and boundary of
In mathematics, a subset of a topological space is called nowhere dense or rare if its closure has empty interior. In a very loose sense, it is a set whose elements are not tightly clustered anywhere. For example, the integers are nowhere dense among the reals, whereas an open ball is not.

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points in the closure of S not belonging to the interior of S. An element of the boundary of S is called a boundary point of S. The term boundary operation refers to finding or taking the boundary of a set. Notations used for boundary of a set S include and . Some authors use the term frontier instead of boundary in an attempt to avoid confusion with a different definition used in algebraic topology and the theory of manifolds. Despite widespread acceptance of the meaning of the terms boundary and frontier, they have sometimes been used to refer to other sets. For example, Metric Spaces by E. T. Copson uses the term boundary to refer to Hausdorff's border, which is defined as the intersection of a set with its boundary. Hausdorff also introduced the term residue, which is defined as the intersection of a set with the closure of the border of its complement.
In mathematics, more specifically in topology, an open map is a function between two topological spaces that maps open sets to open sets. That is, a function is open if for any open set in the image is open in Likewise, a closed map is a function that maps closed sets to closed sets. A map may be open, closed, both, or neither; in particular, an open map need not be closed and vice versa.
In mathematics, a closure operator on a set S is a function :{\mathcal {P}}(S)\rightarrow {\mathcal {P}}(S)} from the power set of S to itself that satisfies the following conditions for all sets
In functional analysis and related areas of mathematics, locally convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of balanced, absorbent, convex sets. Alternatively they can be defined as a vector space with a family of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem to hold, yielding a sufficiently rich theory of continuous linear functionals.
In topology and related areas of mathematics, the neighbourhood system, complete system of neighbourhoods, or neighbourhood filter for a point in a topological space is the collection of all neighbourhoods of
In functional analysis and related areas of mathematics an absorbing set in a vector space is a set which can be "inflated" or "scaled up" to eventually always include any given point of the vector space. Alternative terms are radial or absorbent set. Every neighborhood of the origin in every topological vector space is an absorbing subset.
In the mathematical field of topology, a topological space is usually defined by declaring its open sets. However, this is not necessary, as there are many equivalent axiomatic foundations, each leading to exactly the same concept. For instance, a topological space determines a class of closed sets, of closure and interior operators, and of convergence of various types of objects. Each of these can instead be taken as the primary class of objects, with all of the others directly determined from that new starting point. For example, in Kazimierz Kuratowski's well-known textbook on point-set topology, a topological space is defined as a set together with a certain type of "closure operator," and all other concepts are derived therefrom. Likewise, the neighborhood-based axioms can be retraced to Felix Hausdorff's original definition of a topological space in Grundzüge der Mengenlehre.
In topology and related fields of mathematics, a sequential space is a topological space whose topology can be completely characterized by its convergent/divergent sequences. They can be thought of as spaces that satisfy a very weak axiom of countability, and all first-countable spaces are sequential.
In the mathematical field of topology, a hyperconnected space or irreducible space is a topological space X that cannot be written as the union of two proper closed sets. The name irreducible space is preferred in algebraic geometry.
In topology and related areas of mathematics, a subset A of a topological space X is said to be dense in X if every point of X either belongs to A or else is arbitrarily "close" to a member of A — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it. Formally, is dense in if the smallest closed subset of containing is itself.
In the field of topology, a Fréchet–Urysohn space is a topological space with the property that for every subset the closure of in is identical to the sequential closure of in Fréchet–Urysohn spaces are a special type of sequential space.

Filters in topology, a subfield of mathematics, can be used to study topological spaces and define all basic topological notions such a convergence, continuity, compactness, and more. Filters, which are special families of subsets of some given set, also provide a common framework for defining various types of limits of functions such as limits from the left/right, to infinity, to a point or a set, and many others. Special types of filters called ultrafilters have many useful technical properties and they may often be used in place of arbitrary filters.