Related Research Articles

In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.
The Wedderburn–Etherington numbers are an integer sequence named for Ivor Malcolm Haddon Etherington and Joseph Wedderburn that can be used to count certain kinds of binary trees. The first few numbers in the sequence are
In combinatorics and computer science, covering problems are computational problems that ask whether a certain combinatorial structure 'covers' another, or how large the structure has to be to do that. Covering problems are minimization problems and usually integer linear programs, whose dual problems are called packing problems.
In mathematics, discrepancy theory describes the deviation of a situation from the state one would like it to be in. It is also called the theory of irregularities of distribution. This refers to the theme of classical discrepancy theory, namely distributing points in some space such that they are evenly distributed with respect to some subsets. The discrepancy (irregularity) measures how far a given distribution deviates from an ideal one.
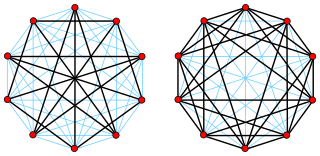
In the mathematical field of graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two distinct vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there.

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is a proper edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.
In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.
In graph theory, a branch of mathematics, the disjoint union of graphs is an operation that combines two or more graphs to form a larger graph. It is analogous to the disjoint union of sets, and is constructed by making the vertex set of the result be the disjoint union of the vertex sets of the given graphs, and by making the edge set of the result be the disjoint union of the edge sets of the given graphs. Any disjoint union of two or more nonempty graphs is necessarily disconnected.

In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :
- Creation of a new vertex v with label i (denoted by i(v))
- Disjoint union of two labeled graphs G and H (denoted by )
- Joining by an edge every vertex labeled i to every vertex labeled j (denoted by η(i,j)), where i ≠ j
- Renaming label i to label j (denoted by ρ(i,j))

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

In graph theory, a branch of mathematics, the linear arboricity of an undirected graph is the smallest number of linear forests its edges can be partitioned into. Here, a linear forest is an acyclic graph with maximum degree two; that is, it is a disjoint union of path graphs. Linear arboricity is a variant of arboricity, the minimum number of forests into which the edges can be partitioned.
In the mathematical area of graph theory, a chordal bipartite graph is a bipartite graph B = (X,Y,E) in which every cycle of length at least 6 in B has a chord, i.e., an edge that connects two vertices that are a distance > 1 apart from each other in the cycle. A better name would be weakly chordal and bipartite since chordal bipartite graphs are in general not chordal as the induced cycle of length 4 shows.

In the mathematical area of graph theory, a k-leaf power of a tree T is a graph G whose vertices are the leaves of T and whose edges connect pairs of leaves whose distance in T is at most k. That is, G is an induced subgraph of the graph power , induced by the leaves of T. For a graph G constructed in this way, T is called a k-leaf root of G.

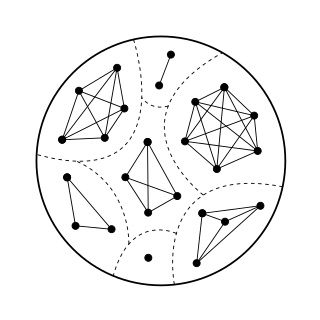
In graph theory, a branch of mathematics, a cluster graph is a graph formed from the disjoint union of complete graphs. Equivalently, a graph is a cluster graph if and only if it has no three-vertex induced path; for this reason, the cluster graphs are also called P3-free graphs. They are the complement graphs of the complete multipartite graphs and the 2-leaf powers. The cluster graphs are transitively closed, and every transitively closed undirected graph is a cluster graph.
Esther M. (Estie) Arkin is an Israeli–American mathematician and computer scientist whose research interests include operations research, computational geometry, combinatorial optimization, and the design and analysis of algorithms. She is a professor of applied mathematics and statistics at Stony Brook University. At Stony Brook, she also directs the undergraduate program in applied mathematics and statistics, and is an affiliated faculty member with the department of computer science.
In graph theory, a matching in a hypergraph is a set of hyperedges, in which every two hyperedges are disjoint. It is an extension of the notion of matching in a graph.
In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.
A sparsity matroid is a mathematical structure that captures how densely a multigraph is populated with edges. To unpack this a little, sparsity is a measure of density of a graph that bounds the number of edges in any subgraph. The property of having a particular matroid as its density measure is invariant under graph isomorphisms and so it is a graph invariant.
Matroid-constrained number partitioning is a variant of the multiway number partitioning problem, in which the subsets in the partition should be independent sets of a matroid. The input to this problem is a set S of items, a positive integer m, and some m matroids over the same set S. The goal is to partition S into m subsets, such that each subset i is an independent set in matroid i. Subject to this constraint, some objective function should be minimized, for example, minimizing the largest sum item sizes in a subset. In a more general variant, each of the m matroids has a weight function, which assigns a weight to each element of the ground-set. Various objective functions have been considered. For each of the three operators max,min,sum, one can use this operator on the weights of items in each subset, and on the subsets themselves. All in all, there are 9 possible objective functions, each of which can be maximized or minimized.
References
- ↑ Cheriyan, Joseph; Jordán, Tibor; Ravi, R. (1999). "On 2-Coverings and 2-Packings of Laminar Families". In Nešetřil, Jaroslav (ed.). Algorithms - ESA' 99. Lecture Notes in Computer Science. Vol. 1643. Berlin, Heidelberg: Springer. pp. 510–520. doi:10.1007/3-540-48481-7_44. ISBN 978-3-540-48481-3.
- ↑ Maduel, Yael; Nutov, Zeev (2010-07-06). "Covering a laminar family by leaf to leaf links". Discrete Applied Mathematics. 158 (13): 1424–1432. doi: 10.1016/j.dam.2010.04.002 . ISSN 0166-218X.
- ↑ Rautenbach, Dieter; Szigeti, Zoltán (2012-08-01). "Greedy colorings of words". Discrete Applied Mathematics. 160 (12): 1872–1874. doi: 10.1016/j.dam.2012.03.038 . ISSN 0166-218X.