In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of higher dimensional Euclidean n-spaces. For lower dimensions n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called n-dimensional volume, n-volume, hypervolume, or simply volume. It is used throughout real analysis, in particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set A is here denoted by λ(A).
In mathematical analysis and in probability theory, a σ-algebra on a set X is a nonempty collection Σ of subsets of X closed under complement, countable unions, and countable intersections. The ordered pair is called a measurable space.
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points, along with an additional structure called a topology, which can be defined as a set of neighbourhoods for each point that satisfy some axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate.
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.

In probability theory, a probability space or a probability triple is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models the throwing of a die.
In mathematics, a base (or basis; pl.: bases) for the topology τ of a topological space (X, τ) is a family of open subsets of X such that every open set of the topology is equal to the union of some sub-family of . For example, the set of all open intervals in the real number line is a basis for the Euclidean topology on because every open interval is an open set, and also every open subset of can be written as a union of some family of open intervals.
In mathematics, and more particularly in set theory, a cover of a set is a family of subsets of whose union is all of . More formally, if is an indexed family of subsets , then is a cover of if . Thus the collection is a cover of if each element of belongs to at least one of the subsets .
In general topology, a branch of mathematics, a non-empty family A of subsets of a set is said to have the finite intersection property (FIP) if the intersection over any finite subcollection of is non-empty. It has the strong finite intersection property (SFIP) if the intersection over any finite subcollection of is infinite. Sets with the finite intersection property are also called centered systems and filter subbases.
In topology, the nerve complex of a set family is an abstract complex that records the pattern of intersections between the sets in the family. It was introduced by Pavel Alexandrov and now has many variants and generalisations, among them the Čech nerve of a cover, which in turn is generalised by hypercoverings. It captures many of the interesting topological properties in an algorithmic or combinatorial way.
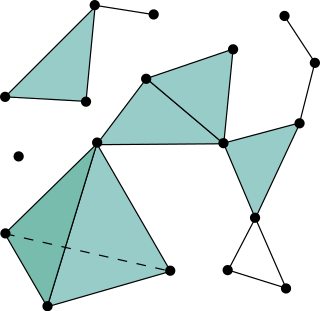
In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.
In combinatorics, a Sperner family, or clutter, is a family F of subsets of a finite set E in which none of the sets contains another. Equivalently, a Sperner family is an antichain in the inclusion lattice over the power set of E. A Sperner family is also sometimes called an independent system or irredundant set.
In mathematics, a field of sets is a mathematical structure consisting of a pair consisting of a set and a family of subsets of called an algebra over that contains the empty set as an element, and is closed under the operations of taking complements in finite unions, and finite intersections.
A Dynkin system, named after Eugene Dynkin, is a collection of subsets of another universal set satisfying a set of axioms weaker than those of 𝜎-algebra. Dynkin systems are sometimes referred to as 𝜆-systems or d-system. These set families have applications in measure theory and probability.
In mathematics, there are two different notions of a ring of sets, both referring to certain families of sets.
In measure theory, Carathéodory's extension theorem states that any pre-measure defined on a given ring of subsets R of a given set Ω can be extended to a measure on the σ-ring generated by R, and this extension is unique if the pre-measure is σ-finite. Consequently, any pre-measure on a ring containing all intervals of real numbers can be extended to the Borel algebra of the set of real numbers. This is an extremely powerful result of measure theory, and leads, for example, to the Lebesgue measure.
In mathematics, a π-system on a set is a collection of certain subsets of such that
In mathematics, especially functional analysis, a bornology on a set X is a collection of subsets of X satisfying axioms that generalize the notion of boundedness. One of the key motivations behind bornologies and bornological analysis is the fact that bornological spaces provide a convenient setting for homological algebra in functional analysis. This is becausepg 9 the category of bornological spaces is additive, complete, cocomplete, and has a tensor product adjoint to an internal hom, all necessary components for homological algebra.
In mathematics, in particular in measure theory, a content is a real-valued function defined on a collection of subsets such that
In mathematics, especially measure theory, a set function is a function whose domain is a family of subsets of some given set and that (usually) takes its values in the extended real number line which consists of the real numbers and

In the mathematical field of set theory, an ultrafilter on a set is a maximal filter on the set In other words, it is a collection of subsets of that satisfies the definition of a filter on and that is maximal with respect to inclusion, in the sense that there does not exist a strictly larger collection of subsets of that is also a filter. Equivalently, an ultrafilter on the set can also be characterized as a filter on with the property that for every subset of either or its complement belongs to the ultrafilter.



















































