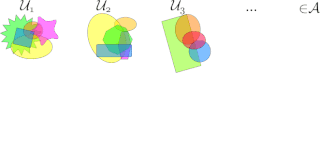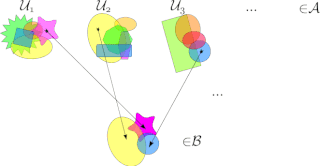In mathematics, the axiom of choice, or AC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of bins, each containing at least one object, it is possible to construct a set by arbitrarily choosing one object from each bin, even if the collection is infinite. Formally, it states that for every indexed family of nonempty sets, there exists an indexed set such that for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.

In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality (size) of sets. The cardinality of a finite set is a natural number: the number of elements in the set. The transfinite cardinal numbers, often denoted using the Hebrew symbol (aleph) followed by a subscript, describe the sizes of infinite sets.
In mathematics, the cardinality of a set is a measure of the "number of elements" of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set is also called its size, when no confusion with other notions of size is possible.
In mathematics, particularly set theory, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting. For example,
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory (ZF) that asserts that the image of any set under any definable mapping is also a set. It is necessary for the construction of certain infinite sets in ZF.
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact with respect to the product topology. The theorem is named after Andrey Nikolayevich Tikhonov, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the remark that its proof was the same as for the special case. The earliest known published proof is contained in a 1935 article of Tychonoff, A., "Uber einen Funktionenraum", Mathematical Annals, 111, pp. 762–766 (1935).

In set theory, an infinite set is a set that is not a finite set. Infinite sets may be countable or uncountable.
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded.

Kőnig's lemma or Kőnig's infinity lemma is a theorem in graph theory due to the Hungarian mathematician Dénes Kőnig who published it in 1927. It gives a sufficient condition for an infinite graph to have an infinitely long path. The computability aspects of this theorem have been thoroughly investigated by researchers in mathematical logic, especially in computability theory. This theorem also has important roles in constructive mathematics and proof theory.
In set theory, an uncountable cardinal is inaccessible if it cannot be obtained from smaller cardinals by the usual operations of cardinal arithmetic. More precisely, a cardinal κ is strongly inaccessible if it is uncountable, it is not a sum of fewer than κ cardinals smaller than κ, and implies .
In mathematics, two sets or classes A and B are equinumerous if there exists a one-to-one correspondence between them, that is, if there exists a function from A to B such that for every element y of B, there is exactly one element x of A with f(x) = y. Equinumerous sets are said to have the same cardinality. The study of cardinality is often called equinumerosity (equalness-of-number). The terms equipollence (equalness-of-strength) and equipotence (equalness-of-power) are sometimes used instead.
In mathematics, a non-measurable set is a set which cannot be assigned a meaningful "volume". The mathematical existence of such sets is construed to provide information about the notions of length, area and volume in formal set theory. In Zermelo–Fraenkel set theory, the axiom of choice entails that non-measurable subsets of exist.
In mathematics, a set A is Dedekind-infinite if some proper subset B of A is equinumerous to A. Explicitly, this means that there exists a bijective function from A onto some proper subset B of A. A set is Dedekind-finite if it is not Dedekind-infinite. Proposed by Dedekind in 1888, Dedekind-infiniteness was the first definition of "infinite" that did not rely on the definition of the natural numbers.
Tarski–Grothendieck set theory is an axiomatic set theory. It is a non-conservative extension of Zermelo–Fraenkel set theory (ZFC) and is distinguished from other axiomatic set theories by the inclusion of Tarski's axiom, which states that for each set there is a Grothendieck universe it belongs to. Tarski's axiom implies the existence of inaccessible cardinals, providing a richer ontology than that of conventional set theories such as ZFC. For example, adding this axiom supports category theory.
This article contains a discussion of paradoxes of set theory. As with most mathematical paradoxes, they generally reveal surprising and counter-intuitive mathematical results, rather than actual logical contradictions within modern axiomatic set theory.
The Banach–Tarski paradox is a theorem in set-theoretic geometry, which states the following: Given a solid ball in three-dimensional space, there exists a decomposition of the ball into a finite number of disjoint subsets, which can then be put back together in a different way to yield two identical copies of the original ball. Indeed, the reassembly process involves only moving the pieces around and rotating them without changing their shape. However, the pieces themselves are not "solids" in the usual sense, but infinite scatterings of points. The reconstruction can work with as few as five pieces.
In mathematics a group is a set together with a binary operation on the set called multiplication that obeys the group axioms. The axiom of choice is an axiom of ZFC set theory which in one form states that every set can be wellordered.
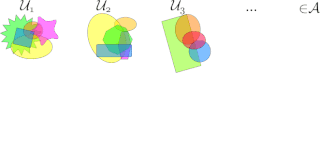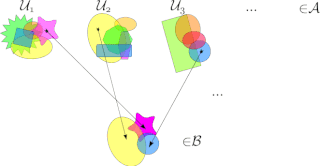
In mathematics, a selection principle is a rule asserting the possibility of obtaining mathematically significant objects by selecting elements from given sequences of sets. The theory of selection principles studies these principles and their relations to other mathematical properties. Selection principles mainly describe covering properties, measure- and category-theoretic properties, and local properties in topological spaces, especially function spaces. Often, the characterization of a mathematical property using a selection principle is a nontrivial task leading to new insights on the characterized property.
In order theory and model theory, branches of mathematics, Cantor's isomorphism theorem states that every two countable dense unbounded linear orders are order-isomorphic. It is named after Georg Cantor, and can be proved by the back-and-forth method sometimes attributed to Cantor, but Cantor's original proof only used the "going forth" half of this method.