In differential geometry, a subject of mathematics, a symplectic manifold is a smooth manifold, , equipped with a closed nondegenerate differential 2-form , called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology. Symplectic manifolds arise naturally in abstract formulations of classical mechanics and analytical mechanics as the cotangent bundles of manifolds. For example, in the Hamiltonian formulation of classical mechanics, which provides one of the major motivations for the field, the set of all possible configurations of a system is modeled as a manifold, and this manifold's cotangent bundle describes the phase space of the system.
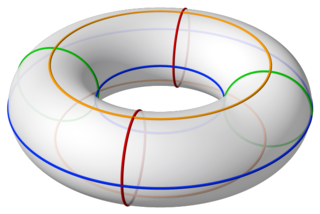
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.

In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise.

In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes. It is a cohomology theory based on the existence of differential forms with prescribed properties.

In mathematics, a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable, or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class Cr it is usually understood that r ≥ 1. The number p is called the dimension of the foliation and q = n − p is called its codimension.
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.
In mathematics, certain systems of partial differential equations are usefully formulated, from the point of view of their underlying geometric and algebraic structure, in terms of a system of differential forms. The idea is to take advantage of the way a differential form restricts to a submanifold, and the fact that this restriction is compatible with the exterior derivative. This is one possible approach to certain over-determined systems, for example, including Lax pairs of integrable systems. A Pfaffian system is specified by 1-forms alone, but the theory includes other types of example of differential system. To elaborate, a Pfaffian system is a set of 1-forms on a smooth manifold.
In mathematics, a Killing vector field, named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold. More simply, the flow generates a symmetry, in the sense that moving each point of an object the same distance in the direction of the Killing vector will not distort distances on the object.
Darboux's theorem is a theorem in the mathematical field of differential geometry and more specifically differential forms, partially generalizing the Frobenius integration theorem. It is a foundational result in several fields, the chief among them being symplectic geometry. The theorem is named after Jean Gaston Darboux who established it as the solution of the Pfaff problem.

In mathematics, a solenoid is a compact connected topological space that may be obtained as the inverse limit of an inverse system of topological groups and continuous homomorphisms
In mathematics, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space V. Its dimension is 1/2n(n + 1). It may be identified with the homogeneous space
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory.

In mathematics, particularly in dynamical systems, Arnold tongues are a pictorial phenomenon that occur when visualizing how the rotation number of a dynamical system, or other related invariant property thereof, changes according to two or more of its parameters. The regions of constant rotation number have been observed, for some dynamical systems, to form geometric shapes that resemble tongues, in which case they are called Arnold tongues.
In the mathematical surgery theory the surgery exact sequence is the main technical tool to calculate the surgery structure set of a compact manifold in dimension . The surgery structure set of a compact -dimensional manifold is a pointed set which classifies -dimensional manifolds within the homotopy type of .
In mathematics, a diffiety is a geometrical object which plays the same role in the modern theory of partial differential equations that algebraic varieties play for algebraic equations, that is, to encode the space of solutions in a more conceptual way. The term was coined in 1984 by Alexandre Mikhailovich Vinogradov as portmanteau from differential variety.
In mathematics a translation surface is a surface obtained from identifying the sides of a polygon in the Euclidean plane by translations. An equivalent definition is a Riemann surface together with a holomorphic 1-form.
In mathematics, the closed-subgroup theorem is a theorem in the theory of Lie groups. It states that if H is a closed subgroup of a Lie group G, then H is an embedded Lie group with the smooth structure agreeing with the embedding. One of several results known as Cartan's theorem, it was first published in 1930 by Élie Cartan, who was inspired by John von Neumann's 1929 proof of a special case for groups of linear transformations.
In mathematics and theoretical physics, and especially gauge theory, the deformed Hermitian Yang–Mills (dHYM) equation is a differential equation describing the equations of motion for a D-brane in the B-model of string theory. The equation was derived by Mariño-Minasian-Moore-Strominger in the case of Abelian gauge group, and by Leung–Yau–Zaslow using mirror symmetry from the corresponding equations of motion for D-branes in the A-model of string theory.
In mathematics, mirror symmetry is a conjectural relationship between certain Calabi–Yau manifolds and a constructed "mirror manifold". The conjecture allows one to relate the number of rational curves on a Calabi-Yau manifold to integrals from a family of varieties. In short, this means there is a relation between the number of genus algebraic curves of degree on a Calabi-Yau variety and integrals on a dual variety . These relations were original discovered by Candelas, De la Ossa, Green, and Parkes in a paper studying a generic quintic threefold in as the variety and a construction from the quintic Dwork family giving . Shortly after, Sheldon Katz wrote a summary paper outlining part of their construction and conjectures what the rigorous mathematical interpretation could be.
In mathematics, and especially symplectic geometry, the Thomas–Yau conjecture asks for the existence of a stability condition, similar to those which appear in algebraic geometry, which guarantees the existence of a solution to the special Lagrangian equation inside a Hamiltonian isotopy class of Lagrangian submanifolds. In particular the conjecture contains two difficulties: first it asks what a suitable stability condition might be, and secondly if one can prove stability of an isotopy class if and only if it contains a special Lagrangian representative.































