Related Research Articles

In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century.
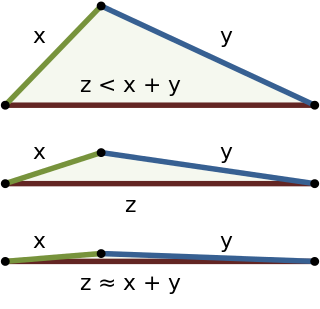
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If x, y, and z are the lengths of the sides of the triangle, with no side being greater than z, then the triangle inequality states that

Hermann Minkowski was a German mathematician and professor at Königsberg, Zürich and Göttingen. He created and developed the geometry of numbers and used geometrical methods to solve problems in number theory, mathematical physics, and the theory of relativity.

Shing-Tung Yau is a Chinese-American mathematician and the William Caspar Graustein Professor of Mathematics at Harvard University. In April 2022, Yau announced retirement from Harvard to become Chair Professor of mathematics at Tsinghua University.
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In -dimensional space the inequality lower bounds the surface area or perimeter of a set by its volume ,
Minkowski, Mińkowski or Minkovski is a surname of Polish origin. It may refer to:

In geometry, the Minkowski sum of two sets of position vectors A and B in Euclidean space is formed by adding each vector in A to each vector in B:

In geometry, Barbier's theorem states that every curve of constant width has perimeter π times its width, regardless of its precise shape. This theorem was first published by Joseph-Émile Barbier in 1860.

The Hasse–Minkowski theorem is a fundamental result in number theory which states that two quadratic forms over a number field are equivalent if and only if they are equivalent locally at all places, i.e. equivalent over every completion of the field. A related result is that a quadratic space over a number field is isotropic if and only if it is isotropic locally everywhere, or equivalently, that a quadratic form over a number field nontrivially represents zero if and only if this holds for all completions of the field. The theorem was proved in the case of the field of rational numbers by Hermann Minkowski and generalized to number fields by Helmut Hasse. The same statement holds even more generally for all global fields.

Louis Nirenberg was a Canadian-American mathematician, considered one of the most outstanding mathematicians of the 20th century.
In mathematics, the Minkowski–Steiner formula is a formula relating the surface area and volume of compact subsets of Euclidean space. More precisely, it defines the surface area as the "derivative" of enclosed volume in an appropriate sense.
In mathematics, the Brunn–Minkowski theorem is an inequality relating the volumes of compact subsets of Euclidean space. The original version of the Brunn–Minkowski theorem applied to convex sets; the generalization to compact nonconvex sets stated here is due to Lazar Lyusternik (1935).
In mathematics, Busemann's theorem is a theorem in Euclidean geometry and geometric tomography. It was first proved by Herbert Busemann in 1949 and was motivated by his theory of area in Finsler spaces.
In mathematics, particularly, in asymptotic convex geometry, Milman's reverse Brunn–Minkowski inequality is a result due to Vitali Milman that provides a reverse inequality to the famous Brunn–Minkowski inequality for convex bodies in n-dimensional Euclidean space Rn. Namely, it bounds the volume of the Minkowski sum of two bodies from above in terms of the volumes of the bodies.
In mathematics, geometric measure theory (GMT) is the study of geometric properties of sets through measure theory. It allows mathematicians to extend tools from differential geometry to a much larger class of surfaces that are not necessarily smooth.
References
- ↑ Finding Lost - Season Four: The Unofficial Guide, Nikki Stafford. Published by ECW Press, 2009; ISBN 1554903505, ISBN 9781554903504, Google Books. Accessed March, 2016.