In mathematics, more specifically in functional analysis, a Banach space is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space.

In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.
The Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a vector subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed vector space to make the study of the dual space "interesting". Another version of the Hahn–Banach theorem is known as the Hahn–Banach separation theorem or the hyperplane separation theorem, and has numerous uses in convex geometry.
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis. A topological vector space is a vector space that is also a topological space with the property that the vector space operations are also continuous functions. Such a topology is called a vector topology and every topological vector space has a uniform topological structure, allowing a notion of uniform convergence and completeness. Some authors also require that the space is a Hausdorff space. One of the most widely studied categories of TVSs are locally convex topological vector spaces. This article focuses on TVSs that are not necessarily locally convex. Banach spaces, Hilbert spaces and Sobolev spaces are other well-known examples of TVSs.
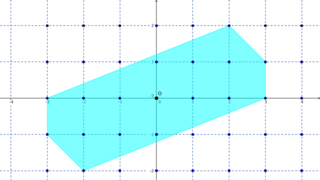
In mathematics, Minkowski's theorem is the statement that every convex set in which is symmetric with respect to the origin and which has volume greater than contains a non-zero integer point. The theorem was proved by Hermann Minkowski in 1889 and became the foundation of the branch of number theory called the geometry of numbers. It can be extended from the integers to any lattice and to any symmetric convex set with volume greater than , where denotes the covolume of the lattice.
In mathematics, a linear form is a linear map from a vector space to its field of scalars.
In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes' theorem.

In mathematics, an extreme point of a convex set in a real or complex vector space is a point in that does not lie in any open line segment joining two points of In linear programming problems, an extreme point is also called vertex or corner point of
In functional analysis and related areas of mathematics, locally convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of balanced, absorbent, convex sets. Alternatively they can be defined as a vector space with a family of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem to hold, yielding a sufficiently rich theory of continuous linear functionals.
In geometry, a zonohedron is a convex polyhedron that is centrally symmetric, every face of which is a polygon that is centrally symmetric. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as a three-dimensional projection of a hypercube. Zonohedra were originally defined and studied by E. S. Fedorove, a Russian crystallographer. More generally, in any dimension, the Minkowski sum of line segments forms a polytope known as a zonotope.
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude of the vector. This norm can be defined as the square root of the inner product of a vector with itself.
In linear algebra, a sublinear function, also called a quasi-seminorm or a Banach functional, on a vector space is a real-valued function with only some of the properties of a seminorm. Unlike seminorms, a sublinear function does not have to be nonnegative-valued and also does not have to be absolutely homogeneous. Seminorms are themselves abstractions of the more well known notion of norms, where a seminorm has all the defining properties of a norm except that it is not required to map non-zero vectors to non-zero values.
In mathematics, Farkas' lemma is a solvability theorem for a finite system of linear inequalities. It was originally proven by the Hungarian mathematician Gyula Farkas. Farkas' lemma is the key result underpinning the linear programming duality and has played a central role in the development of mathematical optimization. It is used amongst other things in the proof of the Karush–Kuhn–Tucker theorem in nonlinear programming. Remarkably, in the area of the foundations of quantum theory, the lemma also underlies the complete set of Bell inequalities in the form of necessary and sufficient conditions for the existence of a local hidden-variable theory, given data from any specific set of measurements.

In the mathematical theory of functional analysis, the Krein–Milman theorem is a proposition about compact convex sets in locally convex topological vector spaces (TVSs).

In geometry, a set in the Euclidean space is called a star domain if there exists an such that for all the line segment from to lies in This definition is immediately generalizable to any real, or complex, vector space.
In mathematics, the Brunn–Minkowski theorem is an inequality relating the volumes of compact subsets of Euclidean space. The original version of the Brunn–Minkowski theorem applied to convex sets; the generalization to compact nonconvex sets stated here is due to Lazar Lyusternik (1935).
In mathematics, the relative interior of a set is a refinement of the concept of the interior, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces.
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.

The Shapley–Folkman lemma is a result in convex geometry that describes the Minkowski addition of sets in a vector space. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the economist Ross M. Starr.
In mathematics, a matroid polytope, also called a matroid basis polytope to distinguish it from other polytopes derived from a matroid, is a polytope constructed via the bases of a matroid. Given a matroid , the matroid polytope is the convex hull of the indicator vectors of the bases of .









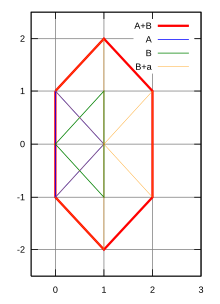







































![An example of a non-convex set such that
A
+
A
[?]
2
A
.
{\displaystyle A+A\neq 2A.} Minkowskisum.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/6/62/Minkowskisum.svg/220px-Minkowskisum.svg.png)





















