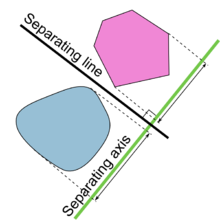
Hyperplane separation theorem

Hyperplane separation theorem

Illustration of the hyperplane separation theorem.
Type	Theorem
Field	Convex geometry Topological vector spaces Collision detection
Conjectured by	Hermann Minkowski
Open problem	No
Generalizations	Hahn–Banach separation theorem

In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in n-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint.

The hyperplane separation theorem is due to Hermann Minkowski. The Hahn–Banach separation theorem generalizes the result to topological vector spaces.

A related result is the supporting hyperplane theorem.

In the context of support-vector machines, the optimally separating hyperplane or maximum-margin hyperplane is a hyperplane which separates two convex hulls of points and is equidistant from the two. ^{[1] [2] [3]}

Statements and proof

In all cases, assume ${\displaystyle A,B}$ to be disjoint, nonempty, and convex subsets of ${\displaystyle \mathbb {R} ^{n}}$. The summary of the results are as follows:

summary table

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle \langle x,v\rangle }$	${\displaystyle \langle y,v\rangle }$
		${\displaystyle \geq c}$	${\displaystyle \leq c}$
closed compact	closed	${\displaystyle >c_{1}}$	${\displaystyle <c_{2}}$ with ${\displaystyle c_{2}<c_{1}}$
closed	closed compact	${\displaystyle >c_{1}}$	${\displaystyle <c_{2}}$ with ${\displaystyle c_{2}<c_{1}}$
open		${\displaystyle >c}$	${\displaystyle \leq c}$
open	open	${\displaystyle >c}$	${\displaystyle <c}$

Hyperplane separation theorem ^[4]  — Let ${\displaystyle A}$ and ${\displaystyle B}$ be two disjoint nonempty convex subsets of ${\displaystyle \mathbb {R} ^{n}}$. Then there exist a nonzero vector ${\displaystyle v}$ and a real number ${\displaystyle c}$ such that

${\displaystyle \langle x,v\rangle \geq c\,{\text{ and }}\langle y,v\rangle \leq c}$

for all ${\displaystyle x}$ in ${\displaystyle A}$ and ${\displaystyle y}$ in ${\displaystyle B}$; i.e., the hyperplane ${\displaystyle \langle \cdot ,v\rangle =c}$, ${\displaystyle v}$ the normal vector, separates ${\displaystyle A}$ and ${\displaystyle B}$.

If both sets are closed, and at least one of them is compact, then the separation can be strict, that is, ${\displaystyle \langle x,v\rangle >c_{1}\,{\text{ and }}\langle y,v\rangle <c_{2}}$ for some ${\displaystyle c_{1}>c_{2}}$

The number of dimensions must be finite. In infinite-dimensional spaces there are examples of two closed, convex, disjoint sets which cannot be separated by a closed hyperplane (a hyperplane where a continuous linear functional equals some constant) even in the weak sense where the inequalities are not strict. ^[5]

Here, the compactness in the hypothesis cannot be relaxed; see an example in the section Counterexamples and uniqueness. This version of the separation theorem does generalize to infinite-dimension; the generalization is more commonly known as the Hahn–Banach separation theorem.

The proof is based on the following lemma:

Lemma — Let ${\displaystyle A}$ and ${\displaystyle B}$ be two disjoint closed subsets of ${\displaystyle \mathbb {R} ^{n}}$, and assume ${\displaystyle A}$ is compact. Then there exist points ${\displaystyle a_{0}\in A}$ and ${\displaystyle b_{0}\in B}$ minimizing the distance ${\displaystyle \|a-b\|}$ over ${\displaystyle a\in A}$ and ${\displaystyle b\in B}$.

Proof of lemma

Let ${\displaystyle a\in A}$ and ${\displaystyle b\in B}$ be any pair of points, and let ${\displaystyle r_{1}=\|b-a\|}$. Since ${\displaystyle A}$ is compact, it is contained in some ball centered on ${\displaystyle a}$; let the radius of this ball be ${\displaystyle r_{2}}$. Let ${\displaystyle S=B\cap {\overline {B_{r_{1}+r_{2}}(a)}}}$ be the intersection of ${\displaystyle B}$ with a closed ball of radius ${\displaystyle r_{1}+r_{2}}$ around ${\displaystyle a}$. Then ${\displaystyle S}$ is compact and nonempty because it contains ${\displaystyle b}$. Since the distance function is continuous, there exist points ${\displaystyle a_{0}}$ and ${\displaystyle b_{0}}$ whose distance ${\displaystyle \|a_{0}-b_{0}\|}$ is the minimum over all pairs of points in ${\displaystyle A\times S}$. It remains to show that ${\displaystyle a_{0}}$ and ${\displaystyle b_{0}}$ in fact have the minimum distance over all pairs of points in ${\displaystyle A\times B}$. Suppose for contradiction that there exist points ${\displaystyle a'}$ and ${\displaystyle b'}$ such that ${\displaystyle \|a'-b'\|<\|a_{0}-b_{0}\|}$. Then in particular, ${\displaystyle \|a'-b'\|<r_{1}}$, and by the triangle inequality, ${\displaystyle \|a-b'\|\leq \|a'-b'\|+\|a-a'\|<r_{1}+r_{2}}$. Therefore ${\displaystyle b'}$ is contained in ${\displaystyle S}$, which contradicts the fact that ${\displaystyle a_{0}}$ and ${\displaystyle b_{0}}$ had minimum distance over ${\displaystyle A\times S}$. ${\displaystyle \square }$

Proof illustration.

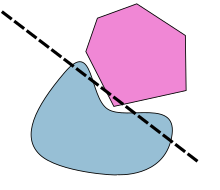
Proof of theorem

We first prove the second case. (See the diagram.)

WLOG, ${\displaystyle A}$ is compact. By the lemma, there exist points ${\displaystyle a_{0}\in A}$ and ${\displaystyle b_{0}\in B}$ of minimum distance to each other. Since ${\displaystyle A}$ and ${\displaystyle B}$ are disjoint, we have ${\displaystyle a_{0}\neq b_{0}}$. Now, construct two hyperplanes ${\displaystyle L_{A},L_{B}}$ perpendicular to line segment ${\displaystyle [a_{0},b_{0}]}$, with ${\displaystyle L_{A}}$ across ${\displaystyle a_{0}}$ and ${\displaystyle L_{B}}$ across ${\displaystyle b_{0}}$. We claim that neither ${\displaystyle A}$ nor ${\displaystyle B}$ enters the space between ${\displaystyle L_{A},L_{B}}$, and thus the perpendicular hyperplanes to ${\displaystyle (a_{0},b_{0})}$ satisfy the requirement of the theorem.

Algebraically, the hyperplanes ${\displaystyle L_{A},L_{B}}$ are defined by the vector ${\displaystyle v:=b_{0}-a_{0}}$, and two constants ${\displaystyle c_{A}:=\langle v,a_{0}\rangle <c_{B}:=\langle v,b_{0}\rangle }$, such that ${\displaystyle L_{A}=\{x:\langle v,x\rangle =c_{A}\},L_{B}=\{x:\langle v,x\rangle =c_{B}\}}$. Our claim is that ${\displaystyle \forall a\in A,\langle v,a\rangle \leq c_{A}}$ and ${\displaystyle \forall b\in B,\langle v,b\rangle \geq c_{B}}$.

Suppose there is some ${\displaystyle a\in A}$ such that ${\displaystyle \langle v,a\rangle >c_{A}}$, then let ${\displaystyle a'}$ be the foot of perpendicular from ${\displaystyle b_{0}}$ to the line segment ${\displaystyle [a_{0},a]}$. Since ${\displaystyle A}$ is convex, ${\displaystyle a'}$ is inside ${\displaystyle A}$, and by planar geometry, ${\displaystyle a'}$ is closer to ${\displaystyle b_{0}}$ than ${\displaystyle a_{0}}$, contradiction. Similar argument applies to ${\displaystyle B}$.

Now for the first case.

Approach both ${\displaystyle A,B}$ from the inside by ${\displaystyle A_{1}\subseteq A_{2}\subseteq \cdots \subseteq A}$ and ${\displaystyle B_{1}\subseteq B_{2}\subseteq \cdots \subseteq B}$, such that each ${\displaystyle A_{k},B_{k}}$ is closed and compact, and the unions are the relative interiors ${\displaystyle \mathrm {relint} (A),\mathrm {relint} (B)}$. (See relative interior page for details.)

Now by the second case, for each pair ${\displaystyle A_{k},B_{k}}$ there exists some unit vector ${\displaystyle v_{k}}$ and real number ${\displaystyle c_{k}}$, such that ${\displaystyle \langle v_{k},A_{k}\rangle <c_{k}<\langle v_{k},B_{k}\rangle }$.

Since the unit sphere is compact, we can take a convergent subsequence, so that ${\displaystyle v_{k}\to v}$. Let ${\displaystyle c_{A}:=\sup _{a\in A}\langle v,a\rangle ,c_{B}:=\inf _{b\in B}\langle v,b\rangle }$. We claim that ${\displaystyle c_{A}\leq c_{B}}$, thus separating ${\displaystyle A,B}$.

Assume not, then there exists some ${\displaystyle a\in A,b\in B}$ such that ${\displaystyle \langle v,a\rangle >\langle v,b\rangle }$, then since ${\displaystyle v_{k}\to v}$, for large enough ${\displaystyle k}$, we have ${\displaystyle \langle v_{k},a\rangle >\langle v_{k},b\rangle }$, contradiction.

Since a separating hyperplane cannot intersect the interiors of open convex sets, we have a corollary:

Separation theorem I — Let ${\displaystyle A}$ and ${\displaystyle B}$ be two disjoint nonempty convex sets. If ${\displaystyle A}$ is open, then there exist a nonzero vector ${\displaystyle v}$ and real number ${\displaystyle c}$ such that

${\displaystyle \langle x,v\rangle >c\,{\text{ and }}\langle y,v\rangle \leq c}$

for all ${\displaystyle x}$ in ${\displaystyle A}$ and ${\displaystyle y}$ in ${\displaystyle B}$. If both sets are open, then there exist a nonzero vector ${\displaystyle v}$ and real number ${\displaystyle c}$ such that

${\displaystyle \langle x,v\rangle >c\,{\text{ and }}\langle y,v\rangle <c}$

for all ${\displaystyle x}$ in ${\displaystyle A}$ and ${\displaystyle y}$ in ${\displaystyle B}$.

Case with possible intersections

If the sets ${\displaystyle A,B}$ have possible intersections, but their relative interiors are disjoint, then the proof of the first case still applies with no change, thus yielding:

Separation theorem II — Let ${\displaystyle A}$ and ${\displaystyle B}$ be two nonempty convex subsets of ${\displaystyle \mathbb {R} ^{n}}$ with disjoint relative interiors. Then there exist a nonzero vector ${\displaystyle v}$ and a real number ${\displaystyle c}$ such that

${\displaystyle \langle x,v\rangle \geq c\,{\text{ and }}\langle y,v\rangle \leq c}$

in particular, we have the supporting hyperplane theorem.

Supporting hyperplane theorem — if ${\displaystyle A}$ is a convex set in ${\displaystyle \mathbb {R} ^{n},}$ and ${\displaystyle a_{0}}$ is a point on the boundary of ${\displaystyle A}$, then there exists a supporting hyperplane of ${\displaystyle A}$ containing ${\displaystyle a_{0}}$.

Proof

If the affine span of ${\displaystyle A}$ is not all of ${\displaystyle \mathbb {R} ^{n}}$, then extend the affine span to a supporting hyperplane. Else, ${\displaystyle \mathrm {relint} (A)=\mathrm {int} (A)}$ is disjoint from ${\displaystyle \mathrm {relint} (\{a_{0}\})=\{a_{0}\}}$, so apply the above theorem.

Converse of theorem

Note that the existence of a hyperplane that only "separates" two convex sets in the weak sense of both inequalities being non-strict obviously does not imply that the two sets are disjoint. Both sets could have points located on the hyperplane.

Counterexamples and uniqueness

The theorem does not apply if one of the bodies is not convex.

If one of A or B is not convex, then there are many possible counterexamples. For example, A and B could be concentric circles. A more subtle counterexample is one in which A and B are both closed but neither one is compact. For example, if A is a closed half plane and B is bounded by one arm of a hyperbola, then there is no strictly separating hyperplane:

${\displaystyle A=\{(x,y):x\leq 0\}}$

${\displaystyle B=\{(x,y):x>0,y\geq 1/x\}.\ }$

(Although, by an instance of the second theorem, there is a hyperplane that separates their interiors.) Another type of counterexample has A compact and B open. For example, A can be a closed square and B can be an open square that touches A.

In the first version of the theorem, evidently the separating hyperplane is never unique. In the second version, it may or may not be unique. Technically a separating axis is never unique because it can be translated; in the second version of the theorem, a separating axis can be unique up to translation.

The horn angle provides a good counterexample to many hyperplane separations. For example, in ${\displaystyle \mathbb {R} ^{2}}$, the unit disk is disjoint from the open interval ${\displaystyle ((1,0),(1,1))}$, but the only line separating them contains the entirety of ${\displaystyle ((1,0),(1,1))}$. This shows that if ${\displaystyle A}$ is closed and ${\displaystyle B}$ is relatively open, then there does not necessarily exist a separation that is strict for ${\displaystyle B}$. However, if ${\displaystyle A}$ is closed polytope then such a separation exists. ^[6]

More variants

Farkas' lemma and related results can be understood as hyperplane separation theorems when the convex bodies are defined by finitely many linear inequalities.

More results may be found. ^[6]

Use in collision detection

In collision detection, the hyperplane separation theorem is usually used in the following form:

Separating axis theorem — Two closed convex objects are disjoint if there exists a line ("separating axis") onto which the two objects' projections are disjoint.

Regardless of dimensionality, the separating axis is always a line. For example, in 3D, the space is separated by planes, but the separating axis is perpendicular to the separating plane.

The separating axis theorem can be applied for fast collision detection between polygon meshes. Each face's normal or other feature direction is used as a separating axis. Note that this yields possible separating axes, not separating lines/planes.

In 3D, using face normals alone will fail to separate some edge-on-edge non-colliding cases. Additional axes, consisting of the cross-products of pairs of edges, one taken from each object, are required. ^[7]

For increased efficiency, parallel axes may be calculated as a single axis.

See also

• Dual cone
• Farkas's lemma
• Kirchberger's theorem
• Optimal control

Notes

1. Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning : Data Mining, Inference, and Prediction (PDF) (Second ed.). New York: Springer. pp. 129–135.
2. Witten, Ian H.; Frank, Eibe; Hall, Mark A.; Pal, Christopher J. (2016). Data Mining: Practical Machine Learning Tools and Techniques (Fourth ed.). Morgan Kaufmann. pp. 253–254. ISBN   9780128043578.
3. Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. pp. 337–338. ISBN   978-1-108-45514-5.
4. Boyd & Vandenberghe 2004, Exercise 2.22.
5. Haïm Brezis, Analyse fonctionnelle : théorie et applications, 1983, remarque 4, p. 7.
6. Stoer, Josef; Witzgall, Christoph (1970). Convexity and Optimization in Finite Dimensions I. Springer Berlin, Heidelberg. (2.12.9). doi:10.1007/978-3-642-46216-0. ISBN   978-3-642-46216-0.
7. "Advanced vector math".

References

• Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (PDF). Cambridge University Press. ISBN   978-0-521-83378-3.
• Golshtein, E. G.; Tretyakov, N.V. (1996). Modified Lagrangians and monotone maps in optimization. New York: Wiley. p. 6. ISBN   0-471-54821-9.
• Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Nondifferentiable and two-level mathematical programming. Boston: Kluwer Academic Publishers. p. 19. ISBN   0-7923-9821-1.

• Soltan, V. (2021). Support and separation properties of convex sets in finite dimension. Extracta Math. Vol. 36, no. 2, 241-278.

External links

• Collision detection and response