In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here, "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems. Not being one-to-one is not considered sufficient for a function to be called one-way.
In data mining and statistics, hierarchical clustering is a method of cluster analysis that seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two categories:
A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random determined by the random bits; thus either the running time, or the output are random variables.
In statistics, the k-nearest neighbors algorithm (k-NN) is a non-parametric supervised learning method first developed by Evelyn Fix and Joseph Hodges in 1951, and later expanded by Thomas Cover. It is used for classification and regression. In both cases, the input consists of the k closest training examples in a data set. The output depends on whether k-NN is used for classification or regression:
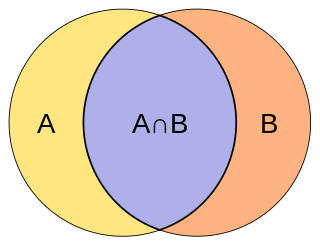
The Jaccard index, also known as the Jaccard similarity coefficient, is a statistic used for gauging the similarity and diversity of sample sets.
The GOST hash function, defined in the standards GOST R 34.11-94 and GOST 34.311-95 is a 256-bit cryptographic hash function. It was initially defined in the Russian national standard GOST R 34.11-94 Information Technology – Cryptographic Information Security – Hash Function. The equivalent standard used by other member-states of the CIS is GOST 34.311-95.
In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. If the primal is a minimization problem then the dual is a maximization problem. Any feasible solution to the primal (minimization) problem is at least as large as any feasible solution to the dual (maximization) problem. Therefore, the solution to the primal is an upper bound to the solution of the dual, and the solution of the dual is a lower bound to the solution of the primal. This fact is called weak duality.
Nearest neighbor search (NNS), as a form of proximity search, is the optimization problem of finding the point in a given set that is closest to a given point. Closeness is typically expressed in terms of a dissimilarity function: the less similar the objects, the larger the function values.
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.
In computer science, streaming algorithms are algorithms for processing data streams in which the input is presented as a sequence of items and can be examined in only a few passes, typically just one. These algorithms are designed to operate with limited memory, generally logarithmic in the size of the stream and/or in the maximum value in the stream, and may also have limited processing time per item.
In discrete mathematics, ideal lattices are a special class of lattices and a generalization of cyclic lattices. Ideal lattices naturally occur in many parts of number theory, but also in other areas. In particular, they have a significant place in cryptography. Micciancio defined a generalization of cyclic lattices as ideal lattices. They can be used in cryptosystems to decrease by a square root the number of parameters necessary to describe a lattice, making them more efficient. Ideal lattices are a new concept, but similar lattice classes have been used for a long time. For example, cyclic lattices, a special case of ideal lattices, are used in NTRUEncrypt and NTRUSign.
In computer science and data mining, MinHash is a technique for quickly estimating how similar two sets are. The scheme was invented by Andrei Broder, and initially used in the AltaVista search engine to detect duplicate web pages and eliminate them from search results. It has also been applied in large-scale clustering problems, such as clustering documents by the similarity of their sets of words.
In computing, the count–min sketch is a probabilistic data structure that serves as a frequency table of events in a stream of data. It uses hash functions to map events to frequencies, but unlike a hash table uses only sub-linear space, at the expense of overcounting some events due to collisions. The count–min sketch was invented in 2003 by Graham Cormode and S. Muthu Muthukrishnan and described by them in a 2005 paper.
Fuzzy extractors are a method that allows biometric data to be used as inputs to standard cryptographic techniques, to enhance computer security. "Fuzzy", in this context, refers to the fact that the fixed values required for cryptography will be extracted from values close to but not identical to the original key, without compromising the security required. One application is to encrypt and authenticate users records, using the biometric inputs of the user as a key.
Similarity learning is an area of supervised machine learning in artificial intelligence. It is closely related to regression and classification, but the goal is to learn a similarity function that measures how similar or related two objects are. It has applications in ranking, in recommendation systems, visual identity tracking, face verification, and speaker verification.
In machine learning, the kernel embedding of distributions comprises a class of nonparametric methods in which a probability distribution is represented as an element of a reproducing kernel Hilbert space (RKHS). A generalization of the individual data-point feature mapping done in classical kernel methods, the embedding of distributions into infinite-dimensional feature spaces can preserve all of the statistical features of arbitrary distributions, while allowing one to compare and manipulate distributions using Hilbert space operations such as inner products, distances, projections, linear transformations, and spectral analysis. This learning framework is very general and can be applied to distributions over any space on which a sensible kernel function may be defined. For example, various kernels have been proposed for learning from data which are: vectors in , discrete classes/categories, strings, graphs/networks, images, time series, manifolds, dynamical systems, and other structured objects. The theory behind kernel embeddings of distributions has been primarily developed by Alex Smola, Le Song , Arthur Gretton, and Bernhard Schölkopf. A review of recent works on kernel embedding of distributions can be found in.
A central problem in algorithmic graph theory is the shortest path problem. One of the generalizations of the shortest path problem is known as the single-source-shortest-paths (SSSP) problem, which consists of finding the shortest paths from a source vertex to all other vertices in the graph. There are classical sequential algorithms which solve this problem, such as Dijkstra's algorithm. In this article, however, we present two parallel algorithms solving this problem.
LSH is a cryptographic hash function designed in 2014 by South Korea to provide integrity in general-purpose software environments such as PCs and smart devices. LSH is one of the cryptographic algorithms approved by the Korean Cryptographic Module Validation Program (KCMVP). And it is the national standard of South Korea.
In computer science, a retrieval data structure, also known as static function, is a space-efficient dictionary-like data type composed of a collection of pairs that allows the following operations:

In mathematics, the Chambolle-Pock algorithm is an algorithm used to solve convex optimization problems. It was introduced by Antonin Chambolle and Thomas Pock in 2011 and has since become a widely used method in various fields, including image processing, computer vision, and signal processing.

















































![th
(
u
,
v
)
p
{\displaystyle {\frac {\theta (u,v)}{\pi }}}
is proportional to
1
-
cos
[?]
(
th
(
u
,
v
)
)
{\displaystyle 1-\cos(\theta (u,v))}
on the interval [0,
p
{\displaystyle \pi } Cosine-distance.png](http://upload.wikimedia.org/wikipedia/commons/thumb/9/9b/Cosine-distance.png/220px-Cosine-distance.png)





































