
In physics the Lorentz force is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge q moving with a velocity v in an electric field E and a magnetic field B experiences a force of

Magnetohydrodynamics is the study of the magnetic properties and behaviour of electrically conducting fluids. Examples of such magnetofluids include plasmas, liquid metals, salt water, and electrolytes. The word magnetohydrodynamics is derived from magneto- meaning magnetic field, hydro- meaning water, and dynamics meaning movement. The field of MHD was initiated by Hannes Alfvén, for which he received the Nobel Prize in Physics in 1970.

In physics, the Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers.

In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
In continuum mechanics, the Froude number is a dimensionless number defined as the ratio of the flow inertia to the external field. The Froude number is based on the speed–length ratio which he defined as:

In physics, circulation is the line integral of a vector field around a closed curve. In fluid dynamics, the field is the fluid velocity field. In electrodynamics, it can be the electric or the magnetic field.
In plasma physics, magnetic helicity is a measure of the linkage, twist, and writhe of a magnetic field. In ideal magnetohydrodynamics, magnetic helicity is conserved. When a magnetic field contains magnetic helicity, it tends to form large-scale structures from small-scale ones. This process can be referred as an inverse transfer in Fourier space.

Magnetic reconnection is a physical process occurring in highly conducting plasmas in which the magnetic topology is rearranged and magnetic energy is converted to kinetic energy, thermal energy, and particle acceleration. Magnetic reconnection occurs on timescales intermediate between slow resistive diffusion of the magnetic field and fast Alfvénic timescales.
The Vlasov equation is a differential equation describing time evolution of the distribution function of plasma consisting of charged particles with long-range interaction, e.g. Coulomb. The equation was first suggested for description of plasma by Anatoly Vlasov in 1938 and later discussed by him in detail in a monograph.
In physics, the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on Brownian motion. The more general form of the equation is
The Magnetic Prandtl number (Prm) is a dimensionless quantity occurring in magnetohydrodynamics which approximates the ratio of momentum diffusivity (viscosity) and magnetic diffusivity. It is defined as:

In fluid dynamics, hydrodynamic stability is the field which analyses the stability and the onset of instability of fluid flows. The study of hydrodynamic stability aims to find out if a given flow is stable or unstable, and if so, how these instabilities will cause the development of turbulence. The foundations of hydrodynamic stability, both theoretical and experimental, were laid most notably by Helmholtz, Kelvin, Rayleigh and Reynolds during the nineteenth century. These foundations have given many useful tools to study hydrodynamic stability. These include Reynolds number, the Euler equations, and the Navier–Stokes equations. When studying flow stability it is useful to understand more simplistic systems, e.g. incompressible and inviscid fluids which can then be developed further onto more complex flows. Since the 1980s, more computational methods are being used to model and analyse the more complex flows.

In fluid mechanics, the Reynolds number is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow. These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation.
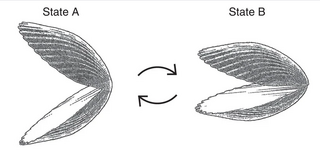
In physics, the scallop theorem states that a swimmer that exhibits time-symmetric motion cannot achieve net displacement in a low-Reynolds number Newtonian fluid environment, i.e. a fluid that is highly viscous. Such a swimmer deforms its body into a particular shape through a sequence of motions and then reverts to the original shape by going through the sequence in reverse. This is known as reciprocal motion and is invariant under time-reversal. Edward Mills Purcell stated this theorem in his 1977 paper Life at Low Reynolds Number explaining physical principles of aquatic locomotion. The theorem is named for the motion of a scallop which opens and closes a simple hinge during one period. Such motion is not sufficient to create migration at low Reynolds numbers. The scallop is an example of a body with one degree of freedom to use for motion. Bodies with a single degree of freedom deform in a reciprocal manner and subsequently, bodies with one degree of freedom do not achieve locomotion in a highly viscous environment.
Magnetohydrodynamic turbulence concerns the chaotic regimes of magnetofluid flow at high Reynolds number. Magnetohydrodynamics (MHD) deals with what is a quasi-neutral fluid with very high conductivity. The fluid approximation implies that the focus is on macro length-and-time scales which are much larger than the collision length and collision time respectively.
The Stuart number (N), also known as magnetic interaction parameter, is a dimensionless number of fluids, i.e. gases or liquids.
In magnetohydrodynamics, Alfvén's theorem, or the frozen-in flux theorem, "states that in a fluid with infinite electric conductivity, the magnetic field is frozen into the fluid and has to move along with it." Hannes Alfvén put the idea forward for the first time in 1942. In his own words: "In view of the infinite conductivity, every motion of the liquid in relation to the lines of force is forbidden because it would give infinite eddy currents. Thus the matter of the liquid is “fastened” to the lines of force...." In later life, Alfvén changed his mind and advised against use of his own theorem. However, Alfvén's theorem is much used today because of a second mechanism, magnetic reconnection. This is a breakdown of Alfvén's theorem in thin current sheets and is important as it can untangle field lines that would become increasingly tangled by plasma velocity shears and vortices in regions of low plasma beta if Alfvén's theorem applied everywhere.
The induction equation, one of the magnetohydrodynamic equations, is a partial differential equation that relates the magnetic field and velocity of an electrically conductive fluid such as a plasma. It can be derived from Maxwell's equations and Ohm's law, and plays a major role in plasma physics and astrophysics, especially in dynamo theory.
Magnetic diffusion refers to the motion of magnetic fields, typically in the presence of a conducting solid or fluid such as a plasma. The motion of magnetic fields is described by the magnetic diffusion equation and is due primarily to induction and diffusion of magnetic fields through the material. The magnetic diffusion equation is a partial differential equation commonly used in physics. Understanding the phenomenon is essential to magnetohydrodynamics and has important consequences in astrophysics, geophysics, and electrical engineering.





































