A difference engine is an automatic mechanical calculator designed to tabulate polynomial functions. It was designed in the 1820s, and was first created by Charles Babbage. The name difference engine is derived from the method of divided differences, a way to interpolate or tabulate functions by using a small set of polynomial co-efficients. Some of the most common mathematical functions used in engineering, science and navigation are built from logarithmic and trigonometric functions, which can be approximated by polynomials, so a difference engine can compute many useful tables.

John Napier of Merchiston, nicknamed Marvellous Merchiston, was a Scottish landowner known as a mathematician, physicist, and astronomer. He was the 8th Laird of Merchiston. His Latinized name was Ioannes Neper.

In mathematics, the logarithm is the inverse function to exponentiation. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 103, the logarithm base 10 of 1000 is 3, or log10 (1000) = 3. The logarithm of x to base b is denoted as logb (x), or without parentheses, logb x, or even without the explicit base, log x, when no confusion is possible, or when the base does not matter such as in big O notation.

A slide rule is a hand-operated mechanical calculator consisting of slidable rulers for evaluating mathematical operations such as multiplication, division, exponents, roots, logarithms, and trigonometry. It is one of the simplest analog computers.

The Sinclair Scientific calculator was a 12-function, pocket-sized scientific calculator introduced in 1974, dramatically undercutting in price other calculators available at the time. The Sinclair Scientific Programmable, released a year later, was advertised as the first budget programmable calculator.

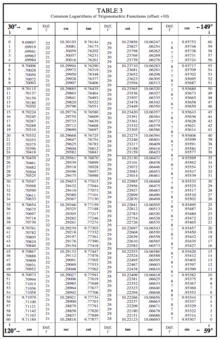
In mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering. The calculation of mathematical tables was an important area of study, which led to the development of the first mechanical computing devices.

In mathematics, the common logarithm is the logarithm with base 10. It is also known as the decadic logarithm and as the decimal logarithm, named after its base, or Briggsian logarithm, after Henry Briggs, an English mathematician who pioneered its use, as well as standard logarithm. Historically, it was known as logarithmus decimalis or logarithmus decadis. It is indicated by log(x), log10(x), or sometimes Log(x) with a capital L; on calculators, it is printed as "log", but mathematicians usually mean natural logarithm (logarithm with base e ≈ 2.71828) rather than common logarithm when writing "log". To mitigate this ambiguity, the ISO 80000 specification recommends that log10(x) should be written lg(x), and loge(x) should be ln(x).

Henry Briggs was an English mathematician notable for changing the original logarithms invented by John Napier into common logarithms, which are sometimes known as Briggsian logarithms in his honour. The specific algorithm for long division in modern use was introduced by Briggs c. 1600 AD.

In mathematics, an identity is an equality relating one mathematical expression A to another mathematical expression B, such that A and B produce the same value for all values of the variables within a certain range of validity. In other words, A = B is an identity if A and B define the same functions, and an identity is an equality between functions that are differently defined. For example, and are identities. Identities are sometimes indicated by the triple bar symbol ≡ instead of =, the equals sign. Formally, an identity is a universally quantified equality.

A scientific calculator is an electronic calculator, either desktop or handheld, designed to perform calculations using basic and complex mathematical operations and functions. They have completely replaced slide rules as well as books of mathematical tables and are used in both educational and professional settings.

The versine or versed sine is a trigonometric function found in some of the earliest trigonometric tables. The versine of an angle is 1 minus its cosine.

CORDIC, also known as Volder's algorithm, or: Digit-by-digit methodCircular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations they require are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.

The SR-50 was Texas Instruments' first scientific pocket calculator with trigonometric and logarithm functions. It enhanced their earlier SR-10 and SR-11 calculators, introduced in 1973, which had featured scientific notation, squares, square root, and reciprocals, but had no trig or log functions, and lacked other features. The SR-50 was introduced in 1974 and sold for US$170. It competed with the Hewlett-Packard HP-35.

The exsecant and excosecant are trigonometric functions defined in terms of the secant and cosecant functions. They used to be important in fields such as surveying, railway engineering, civil engineering, astronomy, and spherical trigonometry and could help improve accuracy, but are rarely used today except to simplify some calculations.

Jost Bürgi, active primarily at the courts in Kassel and Prague, was a Swiss clockmaker, a maker of astronomical instruments and a mathematician.
Prosthaphaeresis was an algorithm used in the late 16th century and early 17th century for approximate multiplication and division using formulas from trigonometry. For the 25 years preceding the invention of the logarithm in 1614, it was the only known generally applicable way of approximating products quickly. Its name comes from the Greek prosthesis (πρόσθεσις) and aphaeresis (ἀφαίρεσις), meaning addition and subtraction, two steps in the process.

The history of logarithms is the story of a correspondence between multiplication on the positive real numbers and addition on the real number line that was formalized in seventeenth century Europe and was widely used to simplify calculation until the advent of the digital computer. The Napierian logarithms were published first in 1614. E. W. Hobson called it "one of the very greatest scientific discoveries that the world has seen." Henry Briggs introduced common logarithms, which were easier to use. Tables of logarithms were published in many forms over four centuries. The idea of logarithms was also used to construct the slide rule, which became ubiquitous in science and engineering until the 1970s. A breakthrough generating the natural logarithm was the result of a search for an expression of area against a rectangular hyperbola, and required the assimilation of a new function into standard mathematics.

Casio fx-3650P is a programmable scientific calculator manufactured by Casio Computer Co., Ltd. It can store 12 digits for the mantissa and 2 digits for the exponent together with the expression each time when the "EXE" button is pressed. Also, the calculator can use the previous result to do calculations by pressing "Ans". It is one of the calculators approved by HKEAA to be used in public examinations in Hong Kong, such as HKDSE.

Trigonometry is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios such as sine.

Mirifici Logarithmorum Canonis Descriptio and Mirifici Logarithmorum Canonis Constructio are two books in Latin by John Napier expounding the method of logarithms. While others had approached the idea of logarithms, notably Jost Bürgi, it was Napier who first published the concept, along with easily used precomputed tables, in his Mirifici Logarithmorum Canonis Descriptio.