
Computational chemistry is a branch of chemistry that uses computer simulations to assist in solving chemical problems. It uses methods of theoretical chemistry incorporated into computer programs to calculate the structures and properties of molecules, groups of molecules, and solids. The importance of this subject stems from the fact that, with the exception of some relatively recent findings related to the hydrogen molecular ion, achieving an accurate quantum mechanical depiction of chemical systems analytically, or in a closed form, is not feasible. The complexity inherent in the many-body problem exacerbates the challenge of providing detailed descriptions of quantum mechanical systems. While computational results normally complement information obtained by chemical experiments, it can occasionally predict unobserved chemical phenomena.
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. The name comes from the Monte Carlo Casino in Monaco, where the primary developer of the method, physicist Stanislaw Ulam, was inspired by his uncle's gambling habits.

Computational physics is the study and implementation of numerical analysis to solve problems in physics. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science. It is sometimes regarded as a subdiscipline of theoretical physics, but others consider it an intermediate branch between theoretical and experimental physics — an area of study which supplements both theory and experiment.
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
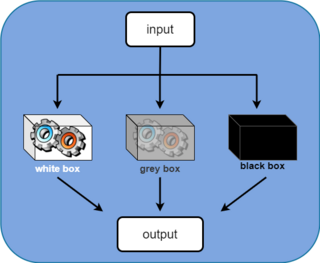
The field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data. System identification also includes the optimal design of experiments for efficiently generating informative data for fitting such models as well as model reduction. A common approach is to start from measurements of the behavior of the system and the external influences and try to determine a mathematical relation between them without going into many details of what is actually happening inside the system; this approach is called black box system identification.
Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).

Finite-difference time-domain (FDTD) or Yee's method is a numerical analysis technique used for modeling computational electrodynamics. Since it is a time-domain method, FDTD solutions can cover a wide frequency range with a single simulation run, and treat nonlinear material properties in a natural way.

The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. The term "butterfly effect" in popular media may stem from the real-world implications of the Lorenz attractor, namely that several different initial chaotic conditions evolve in phase space in a way that never repeats, so all chaos is unpredictable. This underscores that chaotic systems can be completely deterministic and yet still be inherently unpredictable over long periods of time. Because chaos continually increases in systems, we cannot predict the future of systems well. E.g., even the small flap of a butterfly’s wings could set the world on a vastly different trajectory, such as by causing a hurricane. The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to resemble a butterfly.

Fluid–structure interaction (FSI) is the interaction of some movable or deformable structure with an internal or surrounding fluid flow. Fluid–structure interactions can be stable or oscillatory. In oscillatory interactions, the strain induced in the solid structure causes it to move such that the source of strain is reduced, and the structure returns to its former state only for the process to repeat.

In the field of numerical analysis, meshfree methods are those that do not require connection between nodes of the simulation domain, i.e. a mesh, but are rather based on interaction of each node with all its neighbors. As a consequence, original extensive properties such as mass or kinetic energy are no longer assigned to mesh elements but rather to the single nodes. Meshfree methods enable the simulation of some otherwise difficult types of problems, at the cost of extra computing time and programming effort. The absence of a mesh allows Lagrangian simulations, in which the nodes can move according to the velocity field.
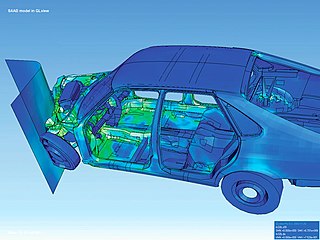
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.
Dynamic mode decomposition (DMD) is a dimensionality reduction algorithm developed by Peter J. Schmid and Joern Sesterhenn in 2008. Given a time series of data, DMD computes a set of modes each of which is associated with a fixed oscillation frequency and decay/growth rate. For linear systems in particular, these modes and frequencies are analogous to the normal modes of the system, but more generally, they are approximations of the modes and eigenvalues of the composition operator. Due to the intrinsic temporal behaviors associated with each mode, DMD differs from dimensionality reduction methods such as principal component analysis, which computes orthogonal modes that lack predetermined temporal behaviors. Because its modes are not orthogonal, DMD-based representations can be less parsimonious than those generated by PCA. However, they can also be more physically meaningful because each mode is associated with a damped sinusoidal behavior in time.

The homotopy analysis method (HAM) is a semi-analytical technique to solve nonlinear ordinary/partial differential equations. The homotopy analysis method employs the concept of the homotopy from topology to generate a convergent series solution for nonlinear systems. This is enabled by utilizing a homotopy-Maclaurin series to deal with the nonlinearities in the system.
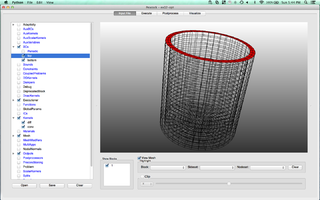
MOOSE is an object-oriented C++ finite element framework for the development of tightly coupled multiphysics solvers from Idaho National Laboratory. MOOSE makes use of the PETSc non-linear solver package and libmesh to provide the finite element discretization.
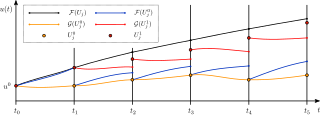
Parareal is a parallel algorithm from numerical analysis and used for the solution of initial value problems. It was introduced in 2001 by Lions, Maday and Turinici. Since then, it has become one of the most widely studied parallel-in-time integration methods.
Nektar++ is a spectral/hp element framework designed to support the construction of efficient high-performance scalable solvers for a wide range of partial differential equations (PDE). The code is released as open-source under the MIT license. Although primarily driven by application-based research, it has been designed as a platform to support the development of novel numerical techniques in the area of high-order finite element methods.
The proper generalized decomposition (PGD) is an iterative numerical method for solving boundary value problems (BVPs), that is, partial differential equations constrained by a set of boundary conditions, such as the Poisson's equation or the Laplace's equation.

Physics-informed neural networks (PINNs) are a type of universal function approximators that can embed the knowledge of any physical laws that govern a given data-set in the learning process, and can be described by partial differential equations (PDEs). They overcome the low data availability of some biological and engineering systems that makes most state-of-the-art machine learning techniques lack robustness, rendering them ineffective in these scenarios. The prior knowledge of general physical laws acts in the training of neural networks (NNs) as a regularization agent that limits the space of admissible solutions, increasing the correctness of the function approximation. This way, embedding this prior information into a neural network results in enhancing the information content of the available data, facilitating the learning algorithm to capture the right solution and to generalize well even with a low amount of training examples.












