Nonelementary integral

Last updated August 13, 2022

In mathematics, a nonelementary antiderivative of a given elementary function is an antiderivative (or indefinite integral) that is, itself, not an elementary function (i.e. a function constructed from a finite number of quotients of constant, algebraic, exponential, trigonometric, and logarithmic functions using field operations).^[1] A theorem by Liouville in 1835 provided the first proof that nonelementary antiderivatives exist.^[2] This theorem also provides a basis for the Risch algorithm for determining (with difficulty) which elementary functions have elementary antiderivatives.

Examples

Examples of functions with nonelementary antiderivatives include:

${\sqrt {1-x^{4}}}$ ^[1] (elliptic integral)
${\frac {1}{\ln x}}$ ^[3] (logarithmic integral)
$e^{-x^{2}}$ ^[1] (error function, Gaussian integral)
$\sin(x^{2})$ and $\cos(x^{2})$ (Fresnel integral)
${\frac {\sin(x)}{x}}=\operatorname {sinc} (x)$ (sine integral, Dirichlet integral)
${\frac {e^{-x}}{x}}$ (exponential integral)
$e^{e^{x}}\,$ (in terms of the exponential integral)
$\ln(\ln x)\,$ (in terms of the logarithmic integral)
${x^{c-1}}e^{-x}$ (incomplete gamma function); for $c=0,$ the antiderivative can be written in terms of the exponential integral; for $c={\tfrac {1}{2}},$ in terms of the error function; for $c=$ any positive integer, the antiderivative is elementary.

Some common non-elementary antiderivative functions are given names, defining so-called special functions, and formulas involving these new functions can express a larger class of non-elementary antiderivatives. The examples above name the corresponding special functions in parentheses.

Properties

Nonelementary antiderivatives can often be evaluated using Taylor series. Even if a function has no elementary antiderivative, its Taylor series can always be integrated term-by-term like a polynomial, giving the antiderivative function as a Taylor series with the same radius of convergence. However, even if the integrand has a convergent Taylor series, its sequence of coefficients often has no elementary formula and must be evaluated term by term, with the same limitation for the integral Taylor series.

Even if it is not possible to evaluate an indefinite integral (antiderivative) in elementary terms, one can always approximate a corresponding definite integral by numerical integration. There are also cases where there is no elementary antiderivative, but specific definite integrals (often improper integrals over unbounded intervals) can be evaluated in elementary terms: most famously the Gaussian integral ${\textstyle \int _{-\infty }^{\infty }e^{-x^{2}}dx={\sqrt {\pi }}.}$

The closure under integration of the set of the elementary functions is the set of the Liouvillian functions.

Related Research Articles

In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function $f$ is a differentiable function $F$ whose derivative is equal to the original function $f$ . This can be stated symbolically as $F' = f$ . The process of solving for antiderivatives is called antidifferentiation, and its opposite operation is called differentiation, which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as $F$ and $G$ .

In mathematics, an elementary function is a function of a single variable that is defined as taking sums, products, and compositions of finitely many polynomial, rational, trigonometric, hyperbolic, and exponential functions, including possibly their inverse functions.

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For any positive integer $n$ ,

The natural logarithm of a number is its logarithm to the base of the mathematical constant $e$ , which is an irrational and transcendental number approximately equal to $2.718 281828459$ . The natural logarithm of $x$ is generally written as $ln x$ , $log e x$ , or sometimes, if the base $e$ is implicit, simply $log x$ . Parentheses are sometimes added for clarity, giving $ln(x)$ , $log e (x)$ , or $log(x)$ . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

In mathematics, the logarithmic integral function or integral logarithm li(x) is a special function. It is relevant in problems of physics and has number theoretic significance. In particular, according to the Siegel–Walfisz theorem it is a very good approximation to the prime-counting function, which is defined as the number of prime numbers less than or equal to a given value $.$

In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation.

In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of definite integrals.

In mathematics, the error function, often denoted by $erf$ , is a complex function of a complex variable defined as:

Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.

In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form

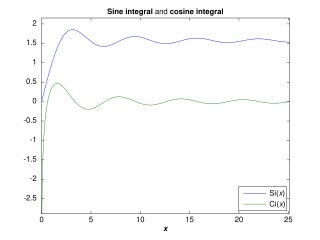
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions.

In symbolic computation, the Risch algorithm is a method of indefinite integration used in some computer algebra systems to find antiderivatives. It is named after the American mathematician Robert Henry Risch, a specialist in computer algebra who developed it in 1968.

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

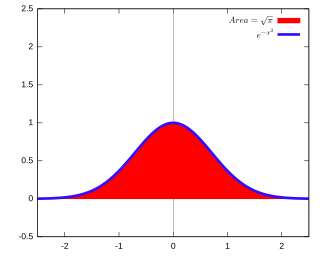
Gaussian integral Integral of the Gaussian function, equal to sqrt(π)

The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function $over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is$

In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations, and functions, but usually no limit, differentiation, or integration. The set of operations and functions may vary with author and context.

In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument.

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:

In mathematics, Liouville's theorem, originally formulated by Joseph Liouville in 1833 to 1841, places an important restriction on antiderivatives that can be expressed as elementary functions.

Carl Johan Malmsten was a Swedish mathematician and politician. He is notable for early research into the theory of functions of a complex variable, for the evaluation of several important logarithmic integrals and series, for his studies in the theory of Zeta-function related series and integrals, as well as for helping Mittag-Leffler start the journal Acta Mathematica. Malmsten became Docent in 1840, and then, Professor of mathematics at the Uppsala University in 1842. He was elected a member of the Royal Swedish Academy of Sciences in 1844. He was also a minister without portfolio in 1859–1866 and Governor of Skaraborg County in 1866–1879.

References

1 2 3 Weisstein, Eric W. "Elementary Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ElementaryFunction.html From MathWorld Accessed 24 Apr 2017.
↑ Dunham, William (2005). The Calculus Gallery. Princeton. p. 119. ISBN 978-0-691-13626-4.
↑ Impossibility theorems for elementary integration; Brian Conrad. Clay Mathematics Institute: 2005 Academy Colloquium Series. Accessed 14 Jul 2014.

Integration of Nonelementary Functions, S.O.S MATHematics.com; accessed 7 Dec 2012.

Nonelementary integral

Contents

Examples

Properties

See also

Related Research Articles

References

Further reading