In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.
In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.

In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
In mathematics, a quadratic equation is an equation that can be rearranged in standard form as

In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.

In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry.

In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic".

In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a property of arithmetic, e.g. "3 + 4 = 4 + 3" or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it ; such operations are not commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A similar property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is symmetric as two equal mathematical objects are equal regardless of their order.

In mathematical analysis, the maximum and minimum of a function are, respectively, the largest and smallest value taken by the function. Known generically as extremum, they may be defined either within a given range or on the entire domain of a function. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions.

In mathematics, the Cantor function is an example of a function that is continuous, but not absolutely continuous. It is a notorious counterexample in analysis, because it challenges naive intuitions about continuity, derivative, and measure. Though it is continuous everywhere and has zero derivative almost everywhere, its value still goes from 0 to 1 as its argument reaches from 0 to 1. Thus, in one sense the function seems very much like a constant one which cannot grow, and in another, it does indeed monotonically grow.

In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero, but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction and at a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function has a critical point at that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the -direction.
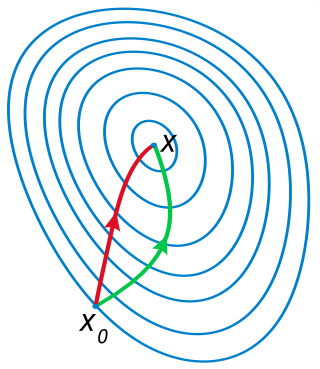
In calculus, Newton's method (also called Newton–Raphson) is an iterative method for finding the roots of a differentiable function F, which are solutions to the equation F (x) = 0. As such, Newton's method can be applied to the derivative f ′ of a twice-differentiable function f to find the roots of the derivative (solutions to f ′(x) = 0), also known as the critical points of f. These solutions may be minima, maxima, or saddle points; see section "Several variables" in Critical point (mathematics) and also section "Geometric interpretation" in this article. This is relevant in optimization, which aims to find (global) minima of the function f.

In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.

In mathematics, a critical point is the argument of a function where the function derivative is zero . The value of the function at a critical point is a critical value.
In mathematics, Robinson arithmetic is a finitely axiomatized fragment of first-order Peano arithmetic (PA), first set out by Raphael M. Robinson in 1950. It is usually denoted Q. Q is almost PA without the axiom schema of mathematical induction. Q is weaker than PA but it has the same language, and both theories are incomplete. Q is important and interesting because it is a finitely axiomatized fragment of PA that is recursively incompletable and essentially undecidable.
In mathematics, a variable is a symbol that represents a mathematical object. A variable may represent a number, a vector, a matrix, a function, the argument of a function, a set, or an element of a set.
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation:

In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their intersection is the point at which they meet. More generally, in set theory, the intersection of sets is defined to be the set of elements which belong to all of them. Unlike the Euclidean definition, this does not presume that the objects under consideration lie in a common space.

In mathematics, the Schwarz lantern is a polyhedral approximation to a cylinder, used as a pathological example of the difficulty of defining the area of a smooth (curved) surface as the limit of the areas of polyhedra. It is formed by stacked rings of isosceles triangles, arranged within each ring in the same pattern as an antiprism. The resulting shape can be folded from paper, and is named after mathematician Hermann Schwarz and for its resemblance to a cylindrical paper lantern. It is also known as Schwarz's boot, Schwarz's polyhedron, or the Chinese lantern.








































