Probabilistic forecasting

Last updated

Probabilistic forecasting summarizes what is known about, or opinions about, future events. In contrast to single-valued forecasts (such as forecasting that the maximum temperature at a given site on a given day will be 23 degrees Celsius, or that the result in a given football match will be a no-score draw), probabilistic forecasts assign a probability to each of a number of different outcomes, and the complete set of probabilities represents a probability forecast. Thus, probabilistic forecasting is a type of probabilistic classification.

Contents

Weather forecasting represents a service in which probability forecasts are sometimes published for public consumption, although it may also be used by weather forecasters as the basis of a simpler type of forecast. For example, forecasters may combine their own experience together with computer-generated probability forecasts to construct a forecast of the type "we expect heavy rainfall".

Sports betting is another field of application where probabilistic forecasting can play a role. The pre-race odds published for a horse race can be considered to correspond to a summary of bettors' opinions about the likely outcome of a race, although this needs to be tempered with caution as bookmakers' profits needs to be taken into account. In sports betting, probability forecasts may not be published as such, but may underlie bookmakers' activities in setting pay-off rates, etc.

Weather forecasting

Probabilistic forecasting is used in a weather forecasting in a number of ways. One of the simplest is the publication of about rainfall in the form of a probability of precipitation.

Ensembles

The probability information is typically derived by using several numerical model runs, with slightly varying initial conditions. This technique is usually referred to as ensemble forecasting by an Ensemble Prediction System (EPS). EPS does not produce a full forecast probability distribution over all possible events, and it is possible to use purely statistical or hybrid statistical/numerical methods to do this. [1] For example, temperature can take on a theoretically infinite number of possible values (events); a statistical method would produce a distribution assigning a probability value to every possible temperature. Implausibly high or low temperatures would then have close to zero probability values.

If it were possible to run the model for every possible set of initial conditions, each with an associated probability, then according to how many members (i.e., individual model runs) of the ensemble predict a certain event, one could compute the actual conditional probability of the given event. In practice, forecasters try to guess a small number of perturbations (usually around 20) that they deem are most likely to yield distinct weather outcomes. Two common techniques for this purpose are breeding vectors (BV) and singular vectors (SV). [2] This technique is not guaranteed to yield an ensemble distribution identical to the actual forecast distribution, but attaining such probabilistic information is one goal of the choice of initial perturbations. Other variants of ensemble forecasting systems that have no immediate probabilistic interpretation include those that assemble the forecasts produced by different numerical weather prediction systems.

Examples

Canada has been one of the first countries to broadcast their probabilistic forecast by giving chances of precipitation in percentages.[ citation needed ] As an example of fully probabilistic forecasts, recently, distribution forecasts of rainfall amounts by purely statistical methods have been developed whose performance is competitive with hybrid EPS[ clarification needed ]/statistical rainfall forecasts of daily rainfall amounts. [3]

Probabilistic forecasting has also been used in combination with neural networks for energy generation. This is done via improved weather forecasting using probabilistic intervals to account for uncertainties in wind and solar forecasting, as opposed to traditional techniques such as point forecasting. [4]

Economic forecasting

Macroeconomic forecasting is the process of making predictions about the economy for key variables such as GDP and inflation, amongst others, and is generally presented as point forecasts. One of the problems with point forecasts is that they do not convey forecast uncertainties, and this is where the role of probability forecasting may be helpful. Most forecasters would attach probabilities to a range of alternative outcomes or scenarios outside of their central forecasts. These probabilities provide a broader assessment of the risk attached to their central forecasts and are influenced by unexpected or extreme shifts in key variables.

Prominent examples of probability forecasting are those undertaken in surveys whereby forecasters are asked, in addition to their central forecasts, for their probability estimates within a specified range. The Monetary Authority of Singapore (MAS) is one such organisation which publishes probability forecasts in its quarterly MAS Survey of Professional Forecasters. Another is Consensus Economics, a macroeconomic survey firm, which publishes a special survey on forecast probabilities [5] each January in its Consensus Forecasts, Asia Pacific Consensus Forecasts and Eastern Europe Consensus Forecasts publications.

Besides survey firms covering this subject, probability forecasts are also a topic of academic research. This was discussed in a 2000 research paper by Anthony Garratt, Kevin Lee, M. Hashem Pesaran and Yongcheol Shin entitled 'Forecast Uncertainties in Macroeconometric Modelling: An Application to the UK Economy'. [6] The MAS released an article on the topic in its Macroeconomic Review in October 2015 called A Brief Survey of Density Forecasting in Macroeconomics. [7]

Energy forecasting

Probabilistic forecasts have not been investigated extensively to date in the context of energy forecasting. However, the situation is changing. [8] [9] While the Global Energy Forecasting Competition (GEFCom) in 2012 was on point forecasting of electric load and wind power, the 2014 edition aimed at probabilistic forecasting of electric load, wind power, solar power and electricity prices. The top two performing teams in the price track of GEFCom2014 used variants of Quantile Regression Averaging (QRA), [10] a new technique which involves applying quantile regression to the point forecasts of a small number of individual forecasting models or experts, hence allows to leverage existing development of point forecasting.

Lumina Decision Systems has created an example probabilistic forecast of energy usage for the next 25 years using the US Department of Energy's Annual Energy Outlook (AEO) 2010.

Population forecasting

Probability forecasts have also been used in the field of population forecasting. [11]

Assessment

Assessing probabilistic forecasts is more complex than assessing deterministic forecasts. [12] If an ensemble-based approach is being used, the individual ensemble members need first to be combined and expressed in terms of a probability distribution. [13] There exist probabilistic (proper) scoring rules such as the continuous ranked probability score for evaluating probabilistic forecasts. [14] One example of such a rule is the Brier score.

See also

Related Research Articles

<span class="mw-page-title-main">Uncertainty</span> Situations involving imperfect or unknown information

Uncertainty refers to epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially observable or stochastic environments, as well as due to ignorance, indolence, or both. It arises in any number of fields, including insurance, philosophy, physics, statistics, economics, finance, medicine, psychology, sociology, engineering, metrology, meteorology, ecology and information science.

In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which a future observation will fall, with a certain probability, given what has already been observed. Prediction intervals are often used in regression analysis.

There are two main uses of the term calibration in statistics that denote special types of statistical inference problems. "Calibration" can mean

<span class="mw-page-title-main">Mathematical statistics</span> Branch of statistics

Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory.

<span class="mw-page-title-main">Weather Prediction Center</span> United States weather agency

The Weather Prediction Center (WPC), located in College Park, Maryland, is one of nine service centers under the umbrella of the National Centers for Environmental Prediction (NCEP), a part of the National Weather Service (NWS), which in turn is part of the National Oceanic and Atmospheric Administration (NOAA) of the U.S. Government. Until March 5, 2013 the Weather Prediction Center was known as the Hydrometeorological Prediction Center (HPC). The Weather Prediction Center serves as a center for quantitative precipitation forecasting, medium range forecasting, and the interpretation of numerical weather prediction computer models.

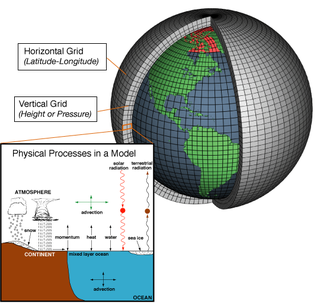
<span class="mw-page-title-main">Numerical weather prediction</span> Weather prediction using mathematical models of the atmosphere and oceans

Numerical weather prediction (NWP) uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic results. A number of global and regional forecast models are run in different countries worldwide, using current weather observations relayed from radiosondes, weather satellites and other observing systems as inputs.

<span class="mw-page-title-main">Ensemble forecasting</span> Multiple simulation method for weather forecasting

Ensemble forecasting is a method used in or within numerical weather prediction. Instead of making a single forecast of the most likely weather, a set of forecasts is produced. This set of forecasts aims to give an indication of the range of possible future states of the atmosphere. Ensemble forecasting is a form of Monte Carlo analysis. The multiple simulations are conducted to account for the two usual sources of uncertainty in forecast models: (1) the errors introduced by the use of imperfect initial conditions, amplified by the chaotic nature of the evolution equations of the atmosphere, which is often referred to as sensitive dependence on initial conditions; and (2) errors introduced because of imperfections in the model formulation, such as the approximate mathematical methods to solve the equations. Ideally, the verified future atmospheric state should fall within the predicted ensemble spread, and the amount of spread should be related to the uncertainty (error) of the forecast. In general, this approach can be used to make probabilistic forecasts of any dynamical system, and not just for weather prediction.

The Brier Score is a strictly proper score function or strictly proper scoring rule that measures the accuracy of probabilistic predictions. For unidimensional predictions, it is strictly equivalent to the mean squared error as applied to predicted probabilities.

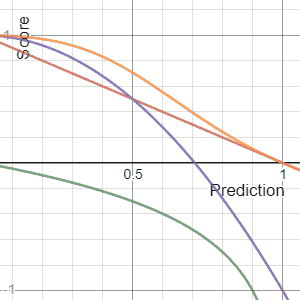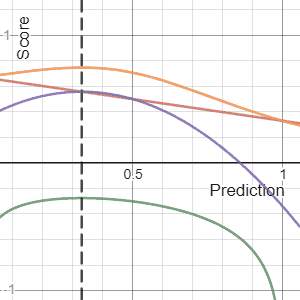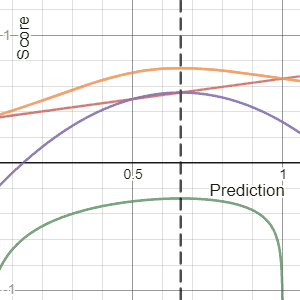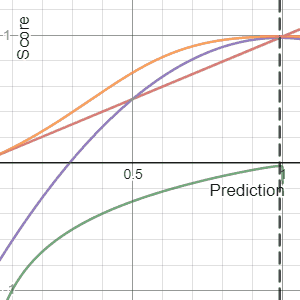
<span class="mw-page-title-main">Scoring rule</span> Measure for evaluating probabilistic forecasts

In decision theory, a scoring rule provides a summary measure for the evaluation of probabilistic predictions or forecasts. It is applicable to tasks in which predictions assign probabilities to events, i.e. one issues a probability distribution as prediction. This includes probabilistic classification of a set of mutually exclusive outcomes or classes.

<span class="mw-page-title-main">Tropical cyclone forecast model</span> Computer program that uses meteorological data to forecast tropical cyclones

A tropical cyclone forecast model is a computer program that uses meteorological data to forecast aspects of the future state of tropical cyclones. There are three types of models: statistical, dynamical, or combined statistical-dynamic. Dynamical models utilize powerful supercomputers with sophisticated mathematical modeling software and meteorological data to calculate future weather conditions. Statistical models forecast the evolution of a tropical cyclone in a simpler manner, by extrapolating from historical datasets, and thus can be run quickly on platforms such as personal computers. Statistical-dynamical models use aspects of both types of forecasting. Four primary types of forecasts exist for tropical cyclones: track, intensity, storm surge, and rainfall. Dynamical models were not developed until the 1970s and the 1980s, with earlier efforts focused on the storm surge problem.

In weather forecasting, model output statistics (MOS) is a multiple linear regression technique in which predictands, often near-surface quantities, are related statistically to one or more predictors. The predictors are typically forecasts from a numerical weather prediction (NWP) model, climatic data, and, if applicable, recent surface observations. Thus, output from NWP models can be transformed by the MOS technique into sensible weather parameters that are familiar to a layperson.

The European Flood Awareness System is a European Commission initiative to increase preparedness for riverine floods across Europe.

<span class="mw-page-title-main">Quantitative precipitation forecast</span> Expected amount of melted precipitation

The quantitative precipitation forecast is the expected amount of melted precipitation accumulated over a specified time period over a specified area. A QPF will be created when precipitation amounts reaching a minimum threshold are expected during the forecast's valid period. Valid periods of precipitation forecasts are normally synoptic hours such as 00:00, 06:00, 12:00 and 18:00 GMT. Terrain is considered in QPFs by use of topography or based upon climatological precipitation patterns from observations with fine detail. Starting in the mid-to-late 1990s, QPFs were used within hydrologic forecast models to simulate impact to rivers throughout the United States. Forecast models show significant sensitivity to humidity levels within the planetary boundary layer, or in the lowest levels of the atmosphere, which decreases with height. QPF can be generated on a quantitative, forecasting amounts, or a qualitative, forecasting the probability of a specific amount, basis. Radar imagery forecasting techniques show higher skill than model forecasts within 6 to 7 hours of the time of the radar image. The forecasts can be verified through use of rain gauge measurements, weather radar estimates, or a combination of both. Various skill scores can be determined to measure the value of the rainfall forecast.

Used in a number of sciences, ranging from econometrics to meteorology, consensus forecasts are predictions of the future that are created by combining several separate forecasts which have often been created using different methodologies. Also known as combining forecasts, forecast averaging or model averaging and committee machines, ensemble averaging or expert aggregation. Applications can range from forecasting the weather to predicting the annual Gross Domestic Product of a country or the number of cars a company or an individual dealer is likely to sell in a year. While forecasts are often made for future values of a time series, they can also be for one-off events such as the outcome of a presidential election or a football match.

<span class="mw-page-title-main">Probabilistic classification</span> Machine learning problem

In machine learning, a probabilistic classifier is a classifier that is able to predict, given an observation of an input, a probability distribution over a set of classes, rather than only outputting the most likely class that the observation should belong to. Probabilistic classifiers provide classification that can be useful in its own right or when combining classifiers into ensembles.

The cost-loss model, also called the cost/loss model or the cost-loss decision model, is a model used to understand how the predicted probability of adverse events affects the decision of whether to take a costly precautionary measure to protect oneself against losses from that event. The threshold probability above which it makes sense to take the precautionary measure equals the ratio of the cost of the preventative measure to the loss averted, and this threshold is termed the cost/loss ratio or cost-loss ratio. The model is typically used in the context of using prediction about weather conditions to decide whether to take a precautionary measure or not.

Quantile Regression Averaging (QRA) is a forecast combination approach to the computation of prediction intervals. It involves applying quantile regression to the point forecasts of a small number of individual forecasting models or experts. It has been introduced in 2014 by Jakub Nowotarski and Rafał Weron and originally used for probabilistic forecasting of electricity prices and loads. Despite its simplicity it has been found to perform extremely well in practice - the top two performing teams in the price track of the Global Energy Forecasting Competition (GEFCom2014) used variants of QRA.

Electricity price forecasting (EPF) is a branch of energy forecasting which focuses on predicting the spot and forward prices in wholesale electricity markets. Over the last 15 years electricity price forecasts have become a fundamental input to energy companies’ decision-making mechanisms at the corporate level.

Non-homogeneous Gaussian regression (NGR) is a type of statistical regression analysis used in the atmospheric sciences as a way to convert ensemble forecasts into probabilistic forecasts. Relative to simple linear regression, NGR uses the ensemble spread as an additional predictor, which is used to improve the prediction of uncertainty and allows the predicted uncertainty to vary from case to case. The prediction of uncertainty in NGR is derived from both past forecast errors statistics and the ensemble spread. NGR was originally developed for site-specific medium range temperature forecasting, but has since also been applied to site-specific medium-range wind forecasting and to seasonal forecasts, and has been adapted for precipitation forecasting. The introduction of NGR was the first demonstration that probabilistic forecasts that take account of the varying ensemble spread could achieve better skill scores than forecasts based on standard Model output statistics approaches applied to the ensemble mean.

References

  1. ↑ Wilks, D.S. (2005), Statistical Methods in the Atmospheric Sciences, Second Edition. (International geophysics series, Volume 91). Academic Press. ISBN   0-12-751966-1
  2. ↑ Toth, Z. and Kalnay, E. (1997), "Ensemble Forecasting at NCEP and the Breeding Method", Monthly Weather Review, 125, pp. 3298.
  3. ↑ Little, M.A. et al. (2009), "Generalized Linear Models for Site-Specific Density Forecasting of UK Daily Rainfall". Monthly Weather Review, 37(3), 1029–1045
  4. ↑ Kabir, H. M. Dipu; Khosravi, Abbas; Hosen, Mohammad Anwar; Nahavandi, Saeid (2018). "Neural Network-Based Uncertainty Quantification: A Survey of Methodologies and Applications". IEEE Access. 6: 36218–36234. doi: 10.1109/access.2018.2836917 . ISSN   2169-3536.
  5. ↑ "Consensus Economics - Economic Forecasts and Indicators".
  6. ↑ Garratt, Anthony; Lee, Kevin; Pesaran, M. Hashem; Shin, Yongcheol (December 2003). "Forecast Uncertainties in Macroeconomic Modeling: An Application to the U.K. Economy" (PDF). Journal of the American Statistical Association. 98 (464): 829–838. doi:10.1198/016214503000000765. JSTOR   30045334. S2CID   120465353 . Retrieved 27 February 2023.
  7. ↑ http://www.mas.gov.sg/~/media/resource/publications/macro_review/2015/MROct15_Macroeconomic%20Review.pdf ,pp. 92-97
  8. ↑ Weron, Rafał (2014). [Open Access]. "Electricity price forecasting: A review of the state-of-the-art with a look into the future". International Journal of Forecasting. 30 (4): 1030–1081. doi: 10.1016/j.ijforecast.2014.08.008 .
  9. ↑ "Call For Papers: Probabilistic Energy Forecasting | International Journal of Forecasting". blog.drhongtao.com. Retrieved 2015-11-29.
  10. ↑ Nowotarski, Jakub; Weron, Rafał (2015). [Open Access]. "Computing electricity spot price prediction intervals using quantile regression and forecast averaging" (PDF). Computational Statistics. 30 (3): 791–803. doi: 10.1007/s00180-014-0523-0 . ISSN   0943-4062.
  11. ↑ Wilson, T.; Bell, M. (2007). "Probabilistic Regional Population Forecasts: The Example of Queensland, Australia". Geographical Analysis. 39: 1–25. doi: 10.1111/j.1538-4632.2006.00693.x .
  12. ↑ Jolliffe, I.T., Stephenson, D.B. (2003) Forecast Verification: A Practitioner's Guide in Atmospheric Science. Wiley. ISBN   0-471-49759-2
  13. ↑ Schölzel, C., A. Hense (2011): Probabilistic assessment of regional climate change in Southwest Germany by ensemble dressing, Climate Dynamics 36 (9), 2003-2014
  14. ↑ Gneiting, T. and Raftery, A.E. (2007), "Strictly Proper Scoring Rules, Prediction, and Estimation". Journal of the American Statistical Association , 102, pp. 359–378
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.