In combinatorial mathematics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling of a sufficiently large complete graph. To demonstrate the theorem for two colours, let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices.

In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.
In combinatorics, the Erdős–Ko–Rado theorem of Paul Erdős, Chao Ko, and Richard Rado is a theorem on intersecting set families.
In arithmetic combinatorics, Szemerédi's theorem is a result concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured that every set of integers A with positive natural density contains a k-term arithmetic progression for every k. Endre Szemerédi proved the conjecture in 1975.
In combinatorics, a Helly family of order k is a family of sets in which every minimal subfamily with an empty intersection has k or fewer sets in it. Equivalently, every finite subfamily such that every k-fold intersection is non-empty has non-empty total intersection. The k-Helly property is the property of being a Helly family of order k.
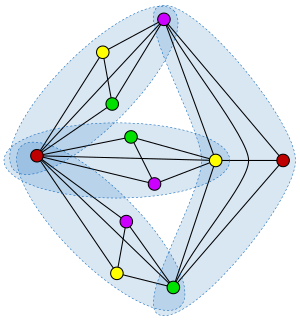
In graph theory, the Erdős–Faber–Lovász conjecture is a problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:
In probability theory, if a large number of events are all independent of one another and each has probability less than 1, then there is a positive probability that none of the events will occur. The Lovász local lemma allows one to relax the independence condition slightly: As long as the events are "mostly" independent from one another and aren't individually too likely, then there will still be a positive probability that none of them occurs. It is most commonly used in the probabilistic method, in particular to give existence proofs.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.
In mathematics, infinitary combinatorics, or combinatorial set theory, is an extension of ideas in combinatorics to infinite sets. Some of the things studied include continuous graphs and trees, extensions of Ramsey's theorem, and Martin's axiom. Recent developments concern combinatorics of the continuum and combinatorics on successors of singular cardinals.
András Hajnal was a professor of mathematics at Rutgers University and a member of the Hungarian Academy of Sciences known for his work in set theory and combinatorics.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that
In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős (1951), after whom it is named.
György Elekes was a Hungarian mathematician and computer scientist who specialized in Combinatorial geometry and Combinatorial set theory. He may be best known for his work in the field that would eventually be called Additive Combinatorics. Particularly notable was his "ingenious" application of the Szemerédi–Trotter theorem to improve the best known lower bound for the sum-product problem. He also proved that any polynomial-time algorithm approximating the volume of convex bodies must have a multiplicative error, and the error grows exponentially on the dimension. With Micha Sharir he set up a framework which eventually led Guth and Katz to the solution of the Erdős distinct distances problem.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.
The Erdős–Gallai theorem is a result in graph theory, a branch of combinatorial mathematics. It provides one of two known approaches to solving the graph realization problem, i.e. it gives a necessary and sufficient condition for a finite sequence of natural numbers to be the degree sequence of a simple graph. A sequence obeying these conditions is called "graphic". The theorem was published in 1960 by Paul Erdős and Tibor Gallai, after whom it is named.
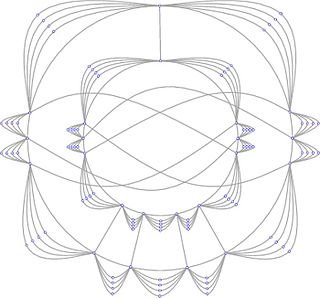
In mathematics, a topological graph is a representation of a graph in the plane, where the vertices of the graph are represented by distinct points and the edges by Jordan arcs joining the corresponding pairs of points. The points representing the vertices of a graph and the arcs representing its edges are called the vertices and the edges of the topological graph. It is usually assumed that any two edges of a topological graph cross a finite number of times, no edge passes through a vertex different from its endpoints, and no two edges touch each other. A topological graph is also called a drawing of a graph.
In graph theory, a branch of mathematics, the Erdős–Hajnal conjecture states that families of graphs defined by forbidden induced subgraphs have either large cliques or large independent sets. It is named for Paul Erdős and András Hajnal.

In graph theory, a branch of mathematics, a half graph is a special type of bipartite graph. These graphs are called the half graphs because they have approximately half of the edges of a complete bipartite graph on the same vertices. The name was given to these graphs by Paul Erdős and András Hajnal.
In graph theory, the Gyárfás–Sumner conjecture asks whether, for every tree and complete graph , the graphs with neither nor as induced subgraphs can be properly colored using only a constant number of colors. Equivalently, it asks whether the -free graphs are -bounded. It is named after András Gyárfás and David Sumner, who formulated it independently in 1975 and 1981 respectively. It remains unproven.














