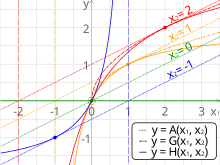
In mathematics and statistics, the arithmetic mean, arithmetic average, or just the mean or average is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results from an experiment, an observational study, or a survey. The term "arithmetic mean" is preferred in some mathematics and statistics contexts because it helps distinguish it from other types of means, such as geometric and harmonic.
In mathematics, the arithmetic–geometric mean of two positive real numbers x and y is the mutual limit of a sequence of arithmetic means and a sequence of geometric means. The arithmetic–geometric mean is used in fast algorithms for exponential, trigonometric functions, and other special functions, as well as some mathematical constants, in particular, computing π.
In statistics, a central tendency is a central or typical value for a probability distribution.

In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite set of real numbers by using the product of their values. The geometric mean is defined as the nth root of the product of n numbers, i.e., for a set of numbers a1, a2, ..., an, the geometric mean is defined as

In mathematics, generalized means are a family of functions for aggregating sets of numbers. These include as special cases the Pythagorean means.
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired.
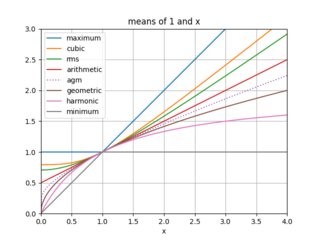
A mean is a numeric quantity representing the center of a collection of numbers and is intermediate to the extreme values of a set of numbers. There are several kinds of means in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value of a given data set.

In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by , , , , or .

In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable X is log-normally distributed, then Y = ln(X) has a normal distribution. Equivalently, if Y has a normal distribution, then the exponential function of Y, X = exp(Y), has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics (e.g., energies, concentrations, lengths, prices of financial instruments, and other metrics).

In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same.
In mathematics, the geometric–harmonic mean M(x, y) of two positive real numbers x and y is defined as follows: we form the geometric mean of g0 = x and h0 = y and call it g1, i.e. g1 is the square root of xy. We also form the harmonic mean of x and y and call it h1, i.e. h1 is the reciprocal of the arithmetic mean of the reciprocals of x and y. These may be done sequentially (in any order) or simultaneously.
In mathematics, Muirhead's inequality, named after Robert Franklin Muirhead, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means.
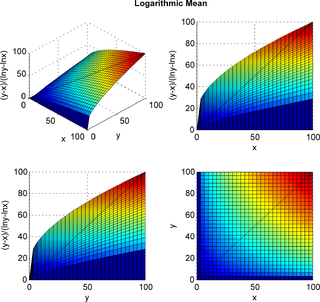
In mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient. This calculation is applicable in engineering problems involving heat and mass transfer.
In mathematics, a contraharmonic mean is a function complementary to the harmonic mean. The contraharmonic mean is a special case of the Lehmer mean, , where p = 2.
In mathematics, a univariate polynomial of degree n with real or complex coefficients has n complex roots, if counted with their multiplicities. They form a multiset of n points in the complex plane. This article concerns the geometry of these points, that is the information about their localization in the complex plane that can be deduced from the degree and the coefficients of the polynomial.

In mathematics, a harmonic progression is a progression formed by taking the reciprocals of an arithmetic progression.
In mathematics and statistics, the Fréchet mean is a generalization of centroids to metric spaces, giving a single representative point or central tendency for a cluster of points. It is named after Maurice Fréchet. Karcher mean is the renaming of the Riemannian Center of Mass construction developed by Karsten Grove and Hermann Karcher. On the real numbers, the arithmetic mean, median, geometric mean, and harmonic mean can all be interpreted as Fréchet means for different distance functions.
For certain applications in linear algebra, it is useful to know properties of the probability distribution of the largest eigenvalue of a finite sum of random matrices. Suppose is a finite sequence of random matrices. Analogous to the well-known Chernoff bound for sums of scalars, a bound on the following is sought for a given parameter t:
In mathematics, a smooth maximum of an indexed family x1, ..., xn of numbers is a smooth approximation to the maximum function meaning a parametric family of functions such that for every α, the function is smooth, and the family converges to the maximum function as . The concept of smooth minimum is similarly defined. In many cases, a single family approximates both: maximum as the parameter goes to positive infinity, minimum as the parameter goes to negative infinity; in symbols, as and as . The term can also be used loosely for a specific smooth function that behaves similarly to a maximum, without necessarily being part of a parametrized family.
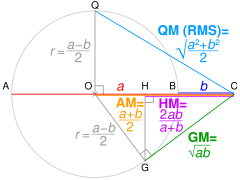
In mathematics, the QM-AM-GM-HM inequalities, also known as the mean inequality chain, state the relationship between the harmonic mean, geometric mean, arithmetic mean, and quadratic mean. Suppose that are positive real numbers. Then