In descriptive statistics and chaos theory, a recurrence plot (RP) is a plot showing, for each moment in time, the times at which the state of a dynamical system returns to the previous state at , i.e., when the phase space trajectory visits roughly the same area in the phase space as at time . In other words, it is a plot of
showing on a horizontal axis and on a vertical axis, where is the state of the system (or its phase space trajectory).
Natural processes can have a distinct recurrent behaviour, e.g. periodicities (as seasonal or Milankovich cycles), but also irregular cyclicities (as El Niño Southern Oscillation, heart beat intervals). Moreover, the recurrence of states, in the meaning that states are again arbitrarily close after some time of divergence, is a fundamental property of deterministic dynamical systems and is typical for nonlinear [ disambiguation needed ] or chaotic systems (cf. Poincaré recurrence theorem). The recurrence of states in nature has been known for a long time and has also been discussed in early work (e.g. Henri Poincaré 1890).
One way to visualize the recurring nature of states by their trajectory through a phase space is the recurrence plot, introduced by Eckmann et al. (1987). Often, the phase space does not have a low enough dimension (two or three) to be pictured, since higher-dimensional phase spaces can only be visualized by projection into the two or three-dimensional sub-spaces. However, making a recurrence plot enables us to investigate certain aspects of the m-dimensional phase space trajectory through a two-dimensional representation.
At a recurrence the trajectory returns to a location (state) in phase space it has visited before up to a small error . The recurrence plot represents the collection of pairs of times such recurrences, i.e., the set of with , with and discrete points of time and the state of the system at time (location of the trajectory at time ). Mathematically, this can be expressed by the binary recurrence matrix
where is a norm and the recurrence threshold. The recurrence plot visualises with coloured (mostly black) dot at coordinates if , with time at the - and -axes.
If only a time series is available, the phase space can be reconstructed by using a time delay embedding (see Takens' theorem):
where is the time series, the embedding dimension and the time delay. Phase space reconstruction is not essential part of the recurrence plot (although often stated in literature), because it is based on phase space trajectories which could be derived from the system's variables directly (e.g., from the three variables of the Lorenz system).
The visual appearance of a recurrence plot gives hints about the dynamics of the system. Caused by characteristic behaviour of the phase space trajectory, a recurrence plot contains typical small-scale structures, as single dots, diagonal lines and vertical/horizontal lines (or a mixture of the latter, which combines to extended clusters). The large-scale structure, also called texture, can be visually characterised by homogenous, periodic, drift or disrupted. For example, the plot can show if the trajectory is strictly periodic with period , then all such pairs of times will be separated by a multiple of and visible as diagonal lines.
The small-scale structures in RPs are used by the recurrence quantification analysis (Zbilut & Webber 1992; Marwan et al. 2002). This quantification allows us to describe the RPs in a quantitative way and to study transitions or nonlinear parameters of the system. In contrast to the heuristic approach of the recurrence quantification analysis, which depends on the choice of the embedding parameters, some dynamical invariants as correlation dimension, K2 entropy or mutual information, which are independent on the embedding, can also be derived from recurrence plots. The base for these dynamical invariants are the recurrence rate and the distribution of the lengths of the diagonal lines.
Close returns plots are similar to recurrence plots. The difference is that the relative time between recurrences is used for the -axis (instead of absolute time).
The main advantage of recurrence plots is that they provide useful information even for short and non-stationary data, where other methods fail.
Multivariate extensions of recurrence plots were developed as cross recurrence plots and joint recurrence plots.
Cross recurrence plots consider the phase space trajectories of two different systems in the same phase space (Marwan & Kurths 2002):
The dimension of both systems must be the same, but the number of considered states (i.e. data length) can be different. Cross recurrence plots compare the occurrences of similar states of two systems. They can be used in order to analyse the similarity of the dynamical evolution between two different systems, to look for similar matching patterns in two systems, or to study the time-relationship of two similar systems, whose time-scale differ (Marwan & Kurths 2005).
Joint recurrence plots are the Hadamard product of the recurrence plots of the considered sub-systems (Romano et al. 2004), e.g. for two systems and the joint recurrence plot is
In contrast to cross recurrence plots, joint recurrence plots compare the simultaneous occurrence of recurrences in two (or more) systems. Moreover, the dimension of the considered phase spaces can be different, but the number of the considered states has to be the same for all the sub-systems. Joint recurrence plots can be used in order to detect phase synchronisation.
 | This article includes a list of general references, but it lacks sufficient corresponding inline citations .(December 2009) |
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.
In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.
In algebra, the dual numbers are a hypercomplex number system first introduced in the 19th century. They are expressions of the form a + bε, where a and b are real numbers, and ε is a symbol taken to satisfy with .
In mathematics, a quadric or quadric surface (quadric hypersurface in higher dimensions), is a generalization of conic sections (ellipses, parabolas, and hyperbolas). It is a hypersurface (of dimension D) in a (D + 1)-dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in D + 1 variables; for example, D = 1 in the case of conic sections. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a degenerate quadric or a reducible quadric.
Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This is the first of two theorems proven by mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries of physical space.
The calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations.
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called canonical transformations, which map canonical coordinate systems into canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself as one of the new canonical momentum coordinates.
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Aleksandr Lyapunov. In simple terms, if the solutions that start out near an equilibrium point stay near forever, then is Lyapunov stable. More strongly, if is Lyapunov stable and all solutions that start out near converge to , then is said to be asymptotically stable. The notion of exponential stability guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge. The idea of Lyapunov stability can be extended to infinite-dimensional manifolds, where it is known as structural stability, which concerns the behavior of different but "nearby" solutions to differential equations. Input-to-state stability (ISS) applies Lyapunov notions to systems with inputs.
The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. Propagators may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.
In chaos theory, the correlation dimension is a measure of the dimensionality of the space occupied by a set of random points, often referred to as a type of fractal dimension.
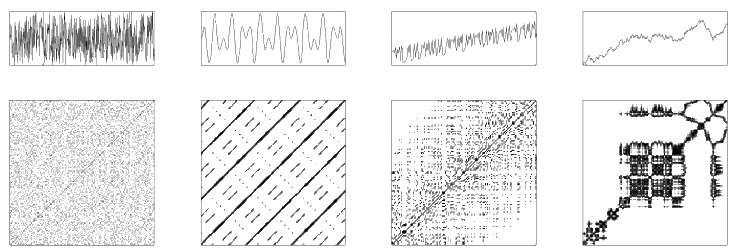
Recurrence quantification analysis (RQA) is a method of nonlinear data analysis for the investigation of dynamical systems. It quantifies the number and duration of recurrences of a dynamical system presented by its phase space trajectory.
In mathematics, more specifically in dynamical systems, the method of averaging exploits systems containing time-scales separation: a fast oscillationversus a slow drift. It suggests that we perform an averaging over a given amount of time in order to iron out the fast oscillations and observe the qualitative behavior from the resulting dynamics. The approximated solution holds under finite time inversely proportional to the parameter denoting the slow time scale. It turns out to be a customary problem where there exists the trade off between how good is the approximated solution balanced by how much time it holds to be close to the original solution.
In chaos theory, the correlation sum is the estimator of the correlation integral, which reflects the mean probability that the states at two different times are close:
In chaos theory, the correlation integral is the mean probability that the states at two different times are close:
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action. It states that the dynamics of a physical system are determined by a variational problem for a functional based on a single function, the Lagrangian, which may contain all physical information concerning the system and the forces acting on it. The variational problem is equivalent to and allows for the derivation of the differential equations of motion of the physical system. Although formulated originally for classical mechanics, Hamilton's principle also applies to classical fields such as the electromagnetic and gravitational fields, and plays an important role in quantum mechanics, quantum field theory and criticality theories.
Recurrence period density entropy (RPDE) is a method, in the fields of dynamical systems, stochastic processes, and time series analysis, for determining the periodicity, or repetitiveness of a signal.
In mathematics, the slow manifold of an equilibrium point of a dynamical system occurs as the most common example of a center manifold. One of the main methods of simplifying dynamical systems, is to reduce the dimension of the system to that of the slow manifold—center manifold theory rigorously justifies the modelling. For example, some global and regional models of the atmosphere or oceans resolve the so-called quasi-geostrophic flow dynamics on the slow manifold of the atmosphere/oceanic dynamics, and is thus crucial to forecasting with a climate model.
In the theory of dynamical systems, the shadowing lemma is a lemma describing the behaviour of pseudo-orbits near a hyperbolic invariant set. Informally, the theory states that every pseudo-orbit stays uniformly close to some true trajectory —in other words, a pseudo-trajectory is "shadowed" by a true one. This suggests that numerical solutions can be trusted to represent the orbits of the dynamical system. However, caution should be exercised as some shadowing trajectories may not always be physically realizable.
{{cite journal}}: CS1 maint: multiple names: authors list (link)