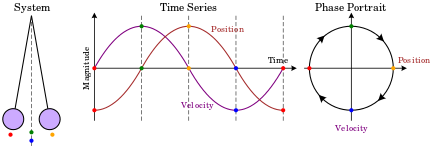
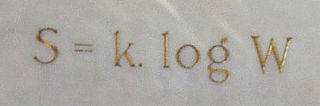Phase space

Last updated November 11, 2024

The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space.^{[ clarification needed ]} The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs.^[1]

Principles

In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-space trajectory for the system) through the high-dimensional space. The phase-space trajectory represents the set of states compatible with starting from one particular initial condition, located in the full phase space that represents the set of states compatible with starting from any initial condition. As a whole, the phase diagram represents all that the system can be, and its shape can easily elucidate qualities of the system that might not be obvious otherwise. A phase space may contain a great number of dimensions. For instance, a gas containing many molecules may require a separate dimension for each particle's x, y and z positions and momenta (6 dimensions for an idealized monatomic gas), and for more complex molecular systems additional dimensions are required to describe vibrational modes of the molecular bonds, as well as spin around 3 axes. Phase spaces are easier to use when analyzing the behavior of mechanical systems restricted to motion around and along various axes of rotation or translation – e.g. in robotics, like analyzing the range of motion of a robotic arm or determining the optimal path to achieve a particular position/momentum result.

Evolution of an ensemble of classical systems in phase space (top). The systems are a massive particle in a one-dimensional potential well (red curve, lower figure). The initially compact ensemble becomes swirled up over time. Hamiltonian flow classical.gif — Evolution of an ensemble of classical systems in phase space (top). The systems are a massive particle in a one-dimensional potential well (red curve, lower figure). The initially compact ensemble becomes swirled up over time.

Conjugate momenta

In classical mechanics, any choice of generalized coordinates q_i for the position (i.e. coordinates on configuration space) defines conjugate generalized momenta p_i, which together define co-ordinates on phase space. More abstractly, in classical mechanics phase space is the cotangent bundle of configuration space, and in this interpretation the procedure above expresses that a choice of local coordinates on configuration space induces a choice of natural local Darboux coordinates for the standard symplectic structure on a cotangent space.

Statistical ensembles in phase space

The motion of an ensemble of systems in this space is studied by classical statistical mechanics. The local density of points in such systems obeys Liouville's theorem, and so can be taken as constant. Within the context of a model system in classical mechanics, the phase-space coordinates of the system at any given time are composed of all of the system's dynamic variables. Because of this, it is possible to calculate the state of the system at any given time in the future or the past, through integration of Hamilton's or Lagrange's equations of motion.

In low dimensions

For simple systems, there may be as few as one or two degrees of freedom. One degree of freedom occurs when one has an autonomous ordinary differential equation in a single variable, $dy/dt=f(y),$ with the resulting one-dimensional system being called a phase line, and the qualitative behaviour of the system being immediately visible from the phase line. The simplest non-trivial examples are the exponential growth model/decay (one unstable/stable equilibrium) and the logistic growth model (two equilibria, one stable, one unstable).

The phase space of a two-dimensional system is called a phase plane, which occurs in classical mechanics for a single particle moving in one dimension, and where the two variables are position and velocity. In this case, a sketch of the phase portrait may give qualitative information about the dynamics of the system, such as the limit cycle of the Van der Pol oscillator shown in the diagram.

Here the horizontal axis gives the position, and vertical axis the velocity. As the system evolves, its state follows one of the lines (trajectories) on the phase diagram.

Phase portrait of the Van der Pol oscillator Limitcycle.svg — Phase portrait of the Van der Pol oscillator

Related concepts

Phase plot

A plot of position and momentum variables as a function of time is sometimes called a phase plot or a phase diagram. However the latter expression, "phase diagram", is more usually reserved in the physical sciences for a diagram showing the various regions of stability of the thermodynamic phases of a chemical system, which consists of pressure, temperature, and composition.

Phase portrait

In mathematics, a phase portrait is a geometric representation of the orbits of a dynamical system in the phase plane. Each set of initial conditions is represented by a different point or curve.

Phase portraits are an invaluable tool in studying dynamical systems. They consist of a plot of typical trajectories in the phase space. This reveals information such as whether an attractor, a repellor or limit cycle is present for the chosen parameter value. The concept of topological equivalence is important in classifying the behaviour of systems by specifying when two different phase portraits represent the same qualitative dynamic behavior. An attractor is a stable point which is also called a "sink". The repeller is considered as an unstable point, which is also known as a "source".

A phase portrait graph of a dynamical system depicts the system's trajectories (with arrows) and stable steady states (with dots) and unstable steady states (with circles) in a phase space. The axes are of state variables.

Phase integral

In classical statistical mechanics (continuous energies) the concept of phase space provides a classical analog to the partition function (sum over states) known as the phase integral.^[2] Instead of summing the Boltzmann factor over discretely spaced energy states (defined by appropriate integer quantum numbers for each degree of freedom), one may integrate over continuous phase space. Such integration essentially consists of two parts: integration of the momentum component of all degrees of freedom (momentum space) and integration of the position component of all degrees of freedom (configuration space). Once the phase integral is known, it may be related to the classical partition function by multiplication of a normalization constant representing the number of quantum energy states per unit phase space. This normalization constant is simply the inverse of the Planck constant raised to a power equal to the number of degrees of freedom for the system.^[3]

Applications

Time-series flow in phase space specified by the differential equation of a pendulum. The X axis corresponds to the pendulum's position, and the Y axis its speed. PenduleEspaceDesPhases.png — Time-series flow in phase space specified by the differential equation of a pendulum. The X axis corresponds to the pendulum's position, and the Y axis its speed.

Chaos theory

Classic examples of phase diagrams from chaos theory are:

the Lorenz attractor
population growth (i.e. logistic map)
parameter plane of complex quadratic polynomials with Mandelbrot set.

Quantum mechanics

In quantum mechanics, the coordinates p and q of phase space normally become Hermitian operators in a Hilbert space.

But they may alternatively retain their classical interpretation, provided functions of them compose in novel algebraic ways (through Groenewold's 1946 star product). This is consistent with the uncertainty principle of quantum mechanics. Every quantum mechanical observable corresponds to a unique function or distribution on phase space, and conversely, as specified by Hermann Weyl (1927) and supplemented by John von Neumann (1931); Eugene Wigner (1932); and, in a grand synthesis, by H. J. Groenewold (1946). With J. E. Moyal (1949), these completed the foundations of the phase-space formulation of quantum mechanics, a complete and logically autonomous reformulation of quantum mechanics.^[4] (Its modern abstractions include deformation quantization and geometric quantization.)

Expectation values in phase-space quantization are obtained isomorphically to tracing operator observables with the density matrix in Hilbert space: they are obtained by phase-space integrals of observables, with the Wigner quasi-probability distribution effectively serving as a measure.

Thus, by expressing quantum mechanics in phase space (the same ambit as for classical mechanics), the Weyl map facilitates recognition of quantum mechanics as a deformation (generalization) of classical mechanics, with deformation parameter ħ /S, where S is the action of the relevant process. (Other familiar deformations in physics involve the deformation of classical Newtonian into relativistic mechanics, with deformation parameter v/c;^{[ citation needed ]} or the deformation of Newtonian gravity into general relativity, with deformation parameter Schwarzschild radius/characteristic dimension.)^{[ citation needed ]}

Classical expressions, observables, and operations (such as Poisson brackets) are modified by ħ-dependent quantum corrections, as the conventional commutative multiplication applying in classical mechanics is generalized to the noncommutative star-multiplication characterizing quantum mechanics and underlying its uncertainty principle.

Thermodynamics and statistical mechanics

In thermodynamics and statistical mechanics contexts, the term "phase space" has two meanings: for one, it is used in the same sense as in classical mechanics. If a thermodynamic system consists of N particles, then a point in the 6N-dimensional phase space describes the dynamic state of every particle in that system, as each particle is associated with 3 position variables and 3 momentum variables. In this sense, as long as the particles are distinguishable, a point in phase space is said to be a microstate of the system. (For indistinguishable particles a microstate consists of a set of N! points, corresponding to all possible exchanges of the N particles.) N is typically on the order of the Avogadro number, thus describing the system at a microscopic level is often impractical. This leads to the use of phase space in a different sense.

The phase space can also refer to the space that is parameterized by the macroscopic states of the system, such as pressure, temperature, etc. For instance, one may view the pressure–volume diagram or temperature–entropy diagram as describing part of this phase space. A point in this phase space is correspondingly called a macrostate. There may easily be more than one microstate with the same macrostate. For example, for a fixed temperature, the system could have many dynamic configurations at the microscopic level. When used in this sense, a phase is a region of phase space where the system in question is in, for example, the liquid phase, or solid phase, etc.

Since there are many more microstates than macrostates, the phase space in the first sense is usually a manifold of much larger dimensions than in the second sense. Clearly, many more parameters are required to register every detail of the system down to the molecular or atomic scale than to simply specify, say, the temperature or the pressure of the system.

Optics

Phase space is extensively used in nonimaging optics,^[5] the branch of optics devoted to illumination. It is also an important concept in Hamiltonian optics.

Medicine

In medicine and bioengineering, the phase space method is used to visualize multidimensional physiological responses.^[6]^[7]

Related Research Articles

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.

The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. This mathematical formalism uses mainly a part of functional analysis, especially Hilbert spaces, which are a kind of linear space. Such are distinguished from mathematical formalisms for physics theories developed prior to the early 1900s by the use of abstract mathematical structures, such as infinite-dimensional Hilbert spaces, and operators on these spaces. In brief, values of physical observables such as energy and momentum were no longer considered as values of functions on phase space, but as eigenvalues; more precisely as spectral values of linear operators in Hilbert space.

Quantization is the systematic transition procedure from a classical understanding of physical phenomena to a newer understanding known as quantum mechanics. It is a procedure for constructing quantum mechanics from classical mechanics. A generalization involving infinite degrees of freedom is field quantization, as in the "quantization of the electromagnetic field", referring to photons as field "quanta". This procedure is basic to theories of atomic physics, chemistry, particle physics, nuclear physics, condensed matter physics, and quantum optics.

The de Broglie–Bohm theory is an interpretation of quantum mechanics which postulates that, in addition to the wavefunction, an actual configuration of particles exists, even when unobserved. The evolution over time of the configuration of all particles is defined by a guiding equation. The evolution of the wave function over time is given by the Schrödinger equation. The theory is named after Louis de Broglie (1892–1987) and David Bohm (1917–1992).

In physics, specifically statistical mechanics, an ensemble is an idealization consisting of a large number of virtual copies of a system, considered all at once, each of which represents a possible state that the real system might be in. In other words, a statistical ensemble is a set of systems of particles used in statistical mechanics to describe a single system. The concept of an ensemble was introduced by J. Willard Gibbs in 1902.

<span class="mw-page-title-main">Wave function</span> Mathematical description of quantum state

In quantum physics, a wave function is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters $ψ$ and $Ψ$ . Wave functions are complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density of measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called normalization. Since the wave function is complex-valued, only its relative phase and relative magnitude can be measured; its value does not, in isolation, tell anything about the magnitudes or directions of measurable observables. One has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function $ψ$ and calculate the statistical distributions for measurable quantities.

In physics, an observable is a physical property or physical quantity that can be measured. In classical mechanics, an observable is a real-valued "function" on the set of all possible system states, e.g., position and momentum. In quantum mechanics, an observable is an operator, or gauge, where the property of the quantum state can be determined by some sequence of operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value.

In physics, action is a scalar quantity that describes how the balance of kinetic versus potential energy of a physical system changes with trajectory. Action is significant because it is an input to the principle of stationary action, an approach to classical mechanics that is simpler for multiple objects. Action and the variational principle are used in Feynman's formulation of quantum mechanics and in general relativity. For systems with small values of action similar to the Planck constant, quantum effects are significant.

The classical limit or correspondence limit is the ability of a physical theory to approximate or "recover" classical mechanics when considered over special values of its parameters. The classical limit is used with physical theories that predict non-classical behavior.

In theoretical physics and mathematical physics, analytical mechanics, or theoretical mechanics is a collection of closely related formulations of classical mechanics. Analytical mechanics uses scalar properties of motion representing the system as a whole—usually its kinetic energy and potential energy. The equations of motion are derived from the scalar quantity by some underlying principle about the scalar's variation.

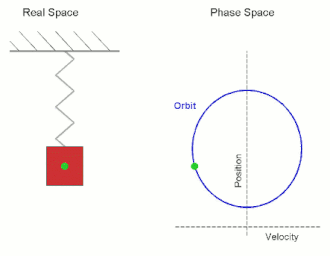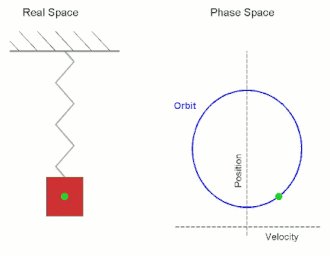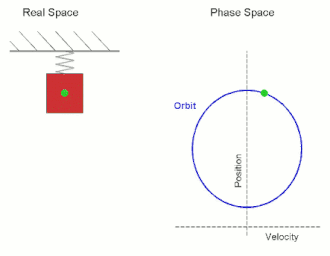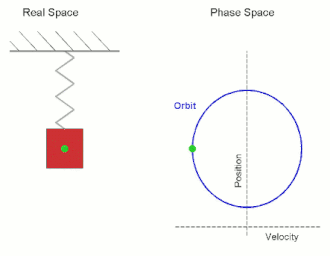
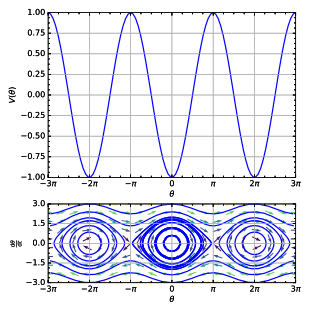
In classical mechanics, the parameters that define the configuration of a system are called generalized coordinates, and the space defined by these coordinates is called the configuration space of the physical system. It is often the case that these parameters satisfy mathematical constraints, such that the set of actual configurations of the system is a manifold in the space of generalized coordinates. This manifold is called the configuration manifold of the system. Notice that this is a notion of "unrestricted" configuration space, i.e. in which different point particles may occupy the same position. In mathematics, in particular in topology, a notion of "restricted" configuration space is mostly used, in which the diagonals, representing "colliding" particles, are removed.

In physics, canonical quantization is a procedure for quantizing a classical theory, while attempting to preserve the formal structure, such as symmetries, of the classical theory to the greatest extent possible.

Conjugate variables are pairs of variables mathematically defined in such a way that they become Fourier transform duals, or more generally are related through Pontryagin duality. The duality relations lead naturally to an uncertainty relation—in physics called the Heisenberg uncertainty principle—between them. In mathematical terms, conjugate variables are part of a symplectic basis, and the uncertainty relation corresponds to the symplectic form. Also, conjugate variables are related by Noether's theorem, which states that if the laws of physics are invariant with respect to a change in one of the conjugate variables, then the other conjugate variable will not change with time . Conjugate variables in thermodynamics are widely used.

In statistical mechanics, a canonical ensemble is the statistical ensemble that represents the possible states of a mechanical system in thermal equilibrium with a heat bath at a fixed temperature. The system can exchange energy with the heat bath, so that the states of the system will differ in total energy.

In physics, complementarity is a conceptual aspect of quantum mechanics that Niels Bohr regarded as an essential feature of the theory. The complementarity principle holds that certain pairs of complementary properties cannot all be observed or measured simultaneously. For example, position and momentum or wave and particle properties. In contemporary terms, complementarity encompasses both the uncertainty principle and wave-particle duality.

In statistical mechanics, a microstate is a specific configuration of a system that describes the precise positions and momenta of all the individual particles or components that make up the system. Each microstate has a certain probability of occurring during the course of the system's thermal fluctuations.

The concept entropy was first developed by German physicist Rudolf Clausius in the mid-nineteenth century as a thermodynamic property that predicts that certain spontaneous processes are irreversible or impossible. In statistical mechanics, entropy is formulated as a statistical property using probability theory. The statistical entropy perspective was introduced in 1870 by Austrian physicist Ludwig Boltzmann, who established a new field of physics that provided the descriptive linkage between the macroscopic observation of nature and the microscopic view based on the rigorous treatment of large ensembles of microscopic states that constitute thermodynamic systems.

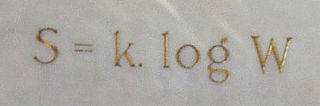
In statistical mechanics, Boltzmann's equation is a probability equation relating the entropy $, also written as, of an ideal gas to the multiplicity, the number of real microstates corresponding to the gas's macrostate:$

In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system.

In physics and geometry, there are two closely related vector spaces, usually three-dimensional but in general of any finite dimension. Position space is the set of all position vectorsr in Euclidean space, and has dimensions of length; a position vector defines a point in space. Momentum space is the set of all momentum vectorsp a physical system can have; the momentum vector of a particle corresponds to its motion, with units of [mass][length][time]⁻¹.

References

↑ Nolte, D. D. (2010). "The tangled tale of phase space". Physics Today. 63 (4): 33–38. Bibcode:2010PhT....63d..33N. doi:10.1063/1.3397041. S2CID 17205307.
↑ Laurendeau, Normand M. (2005). Statistical Thermodynamics: Fundamentals and Applications. New York: Cambridge University Press. ISBN 0-521-84635-8.
↑ Vu-Quoc, L. (2008). "Configuration integral". Archived from the original on April 28, 2012.
↑ Curtright, T. L.; Zachos, C. K. (2012). "Quantum Mechanics in Phase Space". Asia Pacific Physics Newsletter. 01: 37–46. arXiv: 1104.5269 . doi:10.1142/S2251158X12000069. S2CID 119230734.
↑ Chaves, Julio (2015). Introduction to Nonimaging Optics, Second Edition. CRC Press. ISBN 978-1482206739.
↑ Klabukov, I.; Tenchurin, T.; Shepelev, A.; Baranovskii, D.; Mamagulashvili, V.; Dyuzheva, T.; Krasilnikova, O.; Balyasin, M.; Lyundup, A.; Krasheninnikov, M.; Sulina, Y.; Gomzyak, V.; Krasheninnikov, S.; Buzin, A.; Zayratyants, G. (2023). "Biomechanical Behaviors and Degradation Properties of Multilayered Polymer Scaffolds: The Phase Space Method for Bile Duct Design and Bioengineering". Biomedicines. 11 (3): 745. doi: 10.3390/biomedicines11030745 . ISSN 2227-9059. PMC 10044742 . PMID 36979723.
↑ Kirkland, M.A. (2004). "A phase space model of hemopoiesis and the concept of stem cell renewal". Experimental Hematology. 32 (6): 511–519. doi: 10.1016/j.exphem.2004.02.013 . hdl: 10536/DRO/DU:30101092 . ISSN 0301-472X. PMID 15183891.

External links

"Phase space", Encyclopedia of Mathematics , EMS Press, 2001 [1994]

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Nolte, D. D. (2010). "The tangled tale of phase space". Physics Today. 63 (4): 33–38. Bibcode:2010PhT....63d..33N. doi:10.1063/1.3397041. S2CID 17205307.

[2] Laurendeau, Normand M. (2005). Statistical Thermodynamics: Fundamentals and Applications. New York: Cambridge University Press. ISBN 0-521-84635-8.

[3] Vu-Quoc, L. (2008). "Configuration integral". Archived from the original on April 28, 2012.

[4] Curtright, T. L.; Zachos, C. K. (2012). "Quantum Mechanics in Phase Space". Asia Pacific Physics Newsletter. 01: 37–46. arXiv: 1104.5269 . doi:10.1142/S2251158X12000069. S2CID 119230734.

[IntroNio2e-5] Chaves, Julio (2015). Introduction to Nonimaging Optics, Second Edition. CRC Press. ISBN 978-1482206739.

[6] Klabukov, I.; Tenchurin, T.; Shepelev, A.; Baranovskii, D.; Mamagulashvili, V.; Dyuzheva, T.; Krasilnikova, O.; Balyasin, M.; Lyundup, A.; Krasheninnikov, M.; Sulina, Y.; Gomzyak, V.; Krasheninnikov, S.; Buzin, A.; Zayratyants, G. (2023). "Biomechanical Behaviors and Degradation Properties of Multilayered Polymer Scaffolds: The Phase Space Method for Bile Duct Design and Bioengineering". Biomedicines. 11 (3): 745. doi: 10.3390/biomedicines11030745 . ISSN 2227-9059. PMC 10044742 . PMID 36979723.

[7] Kirkland, M.A. (2004). "A phase space model of hemopoiesis and the concept of stem cell renewal". Experimental Hematology. 32 (6): 511–519. doi: 10.1016/j.exphem.2004.02.013 . hdl: 10536/DRO/DU:30101092 . ISSN 0301-472X. PMID 15183891.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Authority control databases
National	Germany United States France BnF data Israel
Other	IdRef