In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent have isomorphic fundamental groups. The fundamental group of a topological space is denoted by .
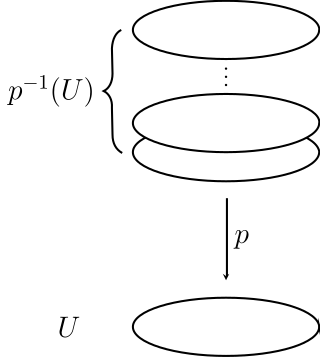
In topology, a covering or covering projection is a map between topological spaces that, intuitively, locally acts like a projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If is a covering, is said to be a covering space or cover of , and is said to be the base of the covering, or simply the base. By abuse of terminology, and may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étale space.
In mathematics, specifically in differential topology, Morse theory enables one to analyze the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a typical differentiable function on a manifold will reflect the topology quite directly. Morse theory allows one to find CW structures and handle decompositions on manifolds and to obtain substantial information about their homology.

In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other. In Euclidean space, the linking number is always an integer, but may be positive or negative depending on the orientation of the two curves.

In mathematics, the braid group on n strands, also known as the Artin braid group, is the group whose elements are equivalence classes of n-braids, and whose group operation is composition of braids. Example applications of braid groups include knot theory, where any knot may be represented as the closure of certain braids ; in mathematical physics where Artin's canonical presentation of the braid group corresponds to the Yang–Baxter equation ; and in monodromy invariants of algebraic geometry.

In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections, the associated holonomy is a type of monodromy and is an inherently global notion. For curved connections, holonomy has nontrivial local and global features.
In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group. These concepts are named after the mathematician J. H. C. Whitehead.
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
In mathematics, in particular in algebraic topology and differential geometry, the Stiefel–Whitney classes are a set of topological invariants of a real vector bundle that describe the obstructions to constructing everywhere independent sets of sections of the vector bundle. Stiefel–Whitney classes are indexed from 0 to n, where n is the rank of the vector bundle. If the Stiefel–Whitney class of index i is nonzero, then there cannot exist everywhere linearly independent sections of the vector bundle. A nonzero nth Stiefel–Whitney class indicates that every section of the bundle must vanish at some point. A nonzero first Stiefel–Whitney class indicates that the vector bundle is not orientable. For example, the first Stiefel–Whitney class of the Möbius strip, as a line bundle over the circle, is not zero, whereas the first Stiefel–Whitney class of the trivial line bundle over the circle, , is zero.
In mathematics, specifically in homotopy theory, a classifying spaceBG of a topological group G is the quotient of a weakly contractible space EG by a proper free action of G. It has the property that any G principal bundle over a paracompact manifold is isomorphic to a pullback of the principal bundle . As explained later, this means that classifying spaces represent a set-valued functor on the homotopy category of topological spaces. The term classifying space can also be used for spaces that represent a set-valued functor on the category of topological spaces, such as Sierpiński space. This notion is generalized by the notion of classifying topos. However, the rest of this article discusses the more commonly used notion of classifying space up to homotopy.
In mathematics, specifically algebraic topology, an Eilenberg–MacLane space is a topological space with a single nontrivial homotopy group.
In an area of mathematics called differential topology, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere. That is, M is a sphere from the point of view of all its topological properties, but carrying a smooth structure that is not the familiar one.
In mathematics, the Thom space,Thom complex, or Pontryagin–Thom construction of algebraic topology and differential topology is a topological space associated to a vector bundle, over any paracompact space.
In mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a complete, finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique. The theorem was proven for closed manifolds by Mostow and extended to finite volume manifolds by Marden (1974) in 3 dimensions, and by Prasad in all dimensions at least 3. Gromov (1981) gave an alternate proof using the Gromov norm. Besson, Courtois & Gallot (1996) gave the simplest available proof.
In mathematics, an operad is a structure that consists of abstract operations, each one having a fixed finite number of inputs (arguments) and one output, as well as a specification of how to compose these operations. Given an operad , one defines an algebra over to be a set together with concrete operations on this set which behave just like the abstract operations of . For instance, there is a Lie operad such that the algebras over are precisely the Lie algebras; in a sense abstractly encodes the operations that are common to all Lie algebras. An operad is to its algebras as a group is to its group representations.
In the mathematical subject of geometric group theory, the Culler–Vogtmann Outer space or just Outer space of a free group Fn is a topological space consisting of the so-called "marked metric graph structures" of volume 1 on Fn. The Outer space, denoted Xn or CVn, comes equipped with a natural action of the group of outer automorphisms Out(Fn) of Fn. The Outer space was introduced in a 1986 paper of Marc Culler and Karen Vogtmann, and it serves as a free group analog of the Teichmüller space of a hyperbolic surface. Outer space is used to study homology and cohomology groups of Out(Fn) and to obtain information about algebraic, geometric and dynamical properties of Out(Fn), of its subgroups and individual outer automorphisms of Fn. The space Xn can also be thought of as the set of Fn-equivariant isometry types of minimal free discrete isometric actions of Fn on Fn on R-treesT such that the quotient metric graph T/Fn has volume 1.
In mathematics, a space, where is a real number, is a specific type of metric space. Intuitively, triangles in a space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature . In a space, the curvature is bounded from above by . A notable special case is ; complete spaces are known as "Hadamard spaces" after the French mathematician Jacques Hadamard.
In mathematics, Reidemeister torsion is a topological invariant of manifolds introduced by Kurt Reidemeister for 3-manifolds and generalized to higher dimensions by Wolfgang Franz and Georges de Rham . Analytic torsion is an invariant of Riemannian manifolds defined by Daniel B. Ray and Isadore M. Singer as an analytic analogue of Reidemeister torsion. Jeff Cheeger and Werner Müller proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds.
In metric geometry, asymptotic dimension of a metric space is a large-scale analog of Lebesgue covering dimension. The notion of asymptotic dimension was introduced by Mikhail Gromov in his 1993 monograph Asymptotic invariants of infinite groups in the context of geometric group theory, as a quasi-isometry invariant of finitely generated groups. As shown by Guoliang Yu, finitely generated groups of finite homotopy type with finite asymptotic dimension satisfy the Novikov conjecture. Asymptotic dimension has important applications in geometric analysis and index theory.
In mathematics, in particular algebraic geometry, Hurwitz spaces are moduli spaces of ramified covers of the projective line, and they are related to the moduli of curves. Their rational points are of interest for the study of the inverse Galois problem, and as such they have been extensively studied by arithmetic geometers. More precisely, Hurwitz spaces classify isomorphism classes of Galois covers with a given automorphism group and a specified number of branch points. The monodromy conjugacy classes at each branch point are also commonly fixed. These spaces have been introduced by Adolf Hurwitz which showed the connectedness of the Hurwitz spaces in the case of simply branched covers.