In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

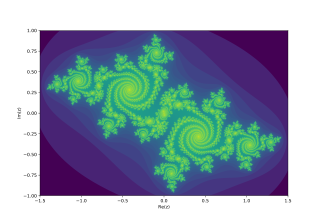
The Mandelbrot set is a two-dimensional set with a relatively simple definition that exhibits great complexity, especially as it is magnified. It is popular for its aesthetic appeal and fractal structures. The set is defined in the complex plane as the complex numbers for which the function does not diverge to infinity when iterated starting at , i.e., for which the sequence , , etc., remains bounded in absolute value.
The fundamental theorem of algebra, also called d'Alembert's theorem or the d'Alembert–Gauss theorem, states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number is a complex number with its imaginary part equal to zero.
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".

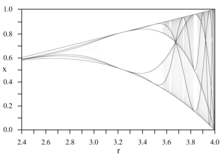
In mathematics, specifically bifurcation theory, the Feigenbaum constants are two mathematical constants which both express ratios in a bifurcation diagram for a non-linear map. They are named after the physicist Mitchell J. Feigenbaum.

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic".

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.
In mathematics, the Schwarzian derivative is an operator similar to the derivative which is invariant under Möbius transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and hypergeometric functions. It plays an important role in the theory of univalent functions, conformal mapping and Teichmüller spaces. It is named after the German mathematician Hermann Schwarz.
This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.

In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.

The Newton fractal is a boundary set in the complex plane which is characterized by Newton's method applied to a fixed polynomial p(Z) ∈ ℂ[Z] or transcendental function. It is the Julia set of the meromorphic function z ↦ z − p(z)/p′(z) which is given by Newton's method. When there are no attractive cycles (of order greater than 1), it divides the complex plane into regions Gk, each of which is associated with a root ζk of the polynomial, k = 1, …, deg(p). In this way the Newton fractal is similar to the Mandelbrot set, and like other fractals it exhibits an intricate appearance arising from a simple description. It is relevant to numerical analysis because it shows that (outside the region of quadratic convergence) the Newton method can be very sensitive to its choice of start point.
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set. Although this curve is only rarely a half-line (ray) it is called a ray because it is an image of a ray.
In mathematics, an orbit portrait is a combinatorial tool used in complex dynamics for understanding the behavior of one-complex dimensional quadratic maps.

In mathematics, the tricorn, sometimes called the Mandelbar set, is a fractal defined in a similar way to the Mandelbrot set, but using the mapping instead of used for the Mandelbrot set. It was introduced by W. D. Crowe, R. Hasson, P. J. Rippon, and P. E. D. Strain-Clark. John Milnor found tricorn-like sets as a prototypical configuration in the parameter space of real cubic polynomials, and in various other families of rational maps.

In mathematics, a Misiurewicz point is a parameter value in the Mandelbrot set and also in real quadratic maps of the interval for which the critical point is strictly pre-periodic. By analogy, the term Misiurewicz point is also used for parameters in a multibrot set where the unique critical point is strictly pre-periodic. This term makes less sense for maps in greater generality that have more than one free critical point because some critical points might be periodic and others not. These points are named after the Polish-American mathematician Michał Misiurewicz, who was the first to study them.
The filled-in Julia set of a polynomial is a Julia set and its interior, non-escaping set.
A Siegel disc or Siegel disk is a connected component in the Fatou set where the dynamics is analytically conjugate to an irrational rotation.

A Douady rabbit is a fractal derived from the Julia set of the function , when parameter is near the center of one of the period three bulbs of the Mandelbrot set for a complex quadratic map. It is named after French mathematician Adrien Douady.

In the mathematical discipline known as complex dynamics, the Herman ring is a Fatou component where the rational function is conformally conjugate to an irrational rotation of the standard annulus.