In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.
Chaos theory is an interdisciplinary scientific theory and branch of mathematics focused on underlying patterns and deterministic laws, of dynamical systems, that are highly sensitive to initial conditions, that were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst. Mathematically, the logistic map is written
In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variablesXi are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin. Every variable Xi in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes ; this generalization is known as the Bernoulli scheme.

In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with initial separation vector diverge at a rate given by

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular. Measure-preserving systems obey the Poincaré recurrence theorem, and are a special case of conservative systems. They provide the formal, mathematical basis for a broad range of physical systems, and, in particular, many systems from classical mechanics as well as systems in thermodynamic equilibrium.

The Hénon map, sometimes called Hénon-Pomeau attractor/map, is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior. The Hénon map takes a point (xn, yn) in the plane and maps it to a new point

In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: mixing paint, mixing drinks, industrial mixing, etc.

In mathematics, the Minkowski question-mark function, denoted by ?(x), is a function possessing various unusual fractal properties, defined by Hermann Minkowski in 1904. It maps quadratic irrational numbers to rational numbers on the unit interval, via an expression relating the continued fraction expansions of the quadratics to the binary expansions of the rationals, given by Arnaud Denjoy in 1938. In addition, it maps rational numbers to dyadic rationals, as can be seen by a recursive definition closely related to the Stern–Brocot tree.

The dyadic transformation is the mapping

The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations originally studied by Otto Rössler in the 1970s. These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor.

The Zaslavskii map is a discrete-time dynamical system introduced by George M. Zaslavsky. It is an example of a dynamical system that exhibits chaotic behavior. The Zaslavskii map takes a point in the plane and maps it to a new point:

The Kaplan–Yorke map is a discrete-time dynamical system. It is an example of a dynamical system that exhibits chaotic behavior. The Kaplan–Yorke map takes a point (xn, yn ) in the plane and maps it to a new point given by
In dynamical systems theory, a period-doubling bifurcation occurs when a slight change in a system's parameters causes a new periodic trajectory to emerge from an existing periodic trajectory—the new one having double the period of the original. With the doubled period, it takes twice as long for the numerical values visited by the system to repeat themselves.
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity.

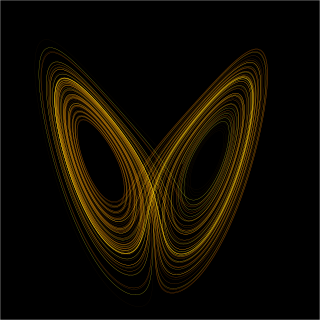
The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In popular media the "butterfly effect" stems from the real-world implications of the Lorenz attractor, namely that in a chaotic physical system, in the absence of perfect knowledge of the initial conditions, our ability to predict its future course will always fail. This underscores that physical systems can be completely deterministic and yet still be inherently unpredictable. The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to resemble a butterfly.
In the mathematical field of dynamical systems, a random dynamical system is a dynamical system in which the equations of motion have an element of randomness to them. Random dynamical systems are characterized by a state space S, a set of maps from S into itself that can be thought of as the set of all possible equations of motion, and a probability distribution Q on the set that represents the random choice of map. Motion in a random dynamical system can be informally thought of as a state evolving according to a succession of maps randomly chosen according to the distribution Q.

In the mathematics of dynamical systems, the double-scroll attractor is a strange attractor observed from a physical electronic chaotic circuit with a single nonlinear resistor. The double-scroll system is often described by a system of three nonlinear ordinary differential equations and a 3-segment piecewise-linear equation. This makes the system easily simulated numerically and easily manifested physically due to Chua's circuits' simple design.





















