Related Research Articles

Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Texas can cause a tornado in Brazil.

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.

Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is: "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle states that classical mechanics is the classical limit of quantum mechanics, specifically in the limit as the ratio of Planck's constant to the action of the system tends to zero. If this is true, then there must be quantum mechanisms underlying classical chaos. If quantum mechanics does not demonstrate an exponential sensitivity to initial conditions, how can exponential sensitivity to initial conditions arise in classical chaos, which must be the correspondence principle limit of quantum mechanics?

In mathematics, the Hénon map, sometimes called Hénon–Pomeau attractor/map, is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior. The Hénon map takes a point (xn, yn) in the plane and maps it to a new point

James A. Yorke is a Distinguished University Research Professor of Mathematics and Physics and former chair of the Mathematics Department at the University of Maryland, College Park.

The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations originally studied by Otto Rössler in the 1970s. These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor. Rössler interpreted it as a formalization of a taffy-pulling machine.

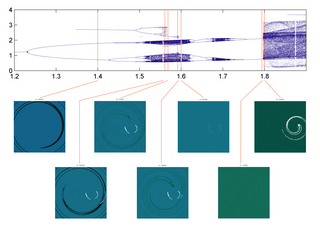
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems and discrete systems.

In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics, or different forms of chaotic dynamics.
The standard map is an area-preserving chaotic map from a square with side onto itself. It is constructed by a Poincaré's surface of section of the kicked rotator, and is defined by:
Cybernetical physics is a scientific area on the border of cybernetics and physics which studies physical systems with cybernetical methods. Cybernetical methods are understood as methods developed within control theory, information theory, systems theory and related areas: control design, estimation, identification, optimization, pattern recognition, signal processing, image processing, etc. Physical systems are also understood in a broad sense; they may be either lifeless, living nature or of artificial (engineering) origin, and must have reasonably understood dynamics and models suitable for posing cybernetical problems. Research objectives in cybernetical physics are frequently formulated as analyses of a class of possible system state changes under external (controlling) actions of a certain class. An auxiliary goal is designing the controlling actions required to achieve a prespecified property change. Among typical control action classes are functions which are constant in time, functions which depend only on time, and functions whose value depends on measurement made at the same time or on previous instances. The last class is of special interest since these functions correspond to system analysis by means of external feedback.
Ogy or OGY may refer to:

Miguel Angel Fernández Sanjuán is a Spanish Theoretical Physicist from Leon, Spain. He is known for his contributions in nonlinear dynamics, chaos theory, and control of chaos, and has published several scientific papers and popular news articles. He has supervised around 20 PhD students in Nonlinear Dynamics, Chaos and Complex Systems.
In applied mathematics and astrodynamics, in the theory of dynamical systems, a crisis is the sudden appearance or disappearance of a strange attractor as the parameters of a dynamical system are varied. This global bifurcation occurs when a chaotic attractor comes into contact with an unstable periodic orbit or its stable manifold. As the orbit approaches the unstable orbit it will diverge away from the previous attractor, leading to a qualitatively different behaviour. Crises can produce intermittent behaviour.
Chaotic scattering is a branch of chaos theory dealing with scattering systems displaying a strong sensitivity to initial conditions. In a classical scattering system there will be one or more impact parameters, b, in which a particle is sent into the scatterer. This gives rise to one or more exit parameters, y, as the particle exits towards infinity. While the particle is traversing the system, there may also be a delay time, T—the time it takes for the particle to exit the system—in addition to the distance travelled, s. In certain systems the two will be equivalent—see below. In a chaotic scattering system, a minute change in the impact parameter, may give rise to a very large change in the exit parameters.

Quantum scarring refers to a phenomenon where the eigenstates of a classically chaotic quantum system have enhanced probability density around the paths of unstable classical periodic orbits. The instability of the periodic orbit is a decisive point that differentiates quantum scars from the more trivial observation that the probability density is enhanced in the neighborhood of stable periodic orbits. The latter can be understood as a purely classical phenomenon, a manifestation of the Bohr correspondence principle, whereas in the former, quantum interference is essential. As such, scarring is both a visual example of quantum-classical correspondence, and simultaneously an example of a (local) quantum suppression of chaos.
Celso Grebogi is a Brazilian theoretical physicist who works in the area of chaos theory. He is one among the pioneers in the nonlinear and complex systems and chaos theory. Currently he works at the University of Aberdeen as the "Sixth Century Chair in Nonlinear and Complex Systems". He has done extensive research in the field of plasma physics before his work on the theory of dynamical systems. He and his colleagues have shown with a numerical example that one can convert a chaotic attractor to any one of numerous possible attracting time-periodic motions by making only small time-dependent perturbations of an available system parameter. This article is considered as one among the classic works in the control theory of chaos and their control method is known as the OGY method. He was listed in the 2016 Thomson Reuters Citation Laureates.

Edward Ott is an American physicist most noted for his contributions to the development of chaos theory.
In the mathematics of chaotic dynamical systems, in the Pyragas method of stabilizing a periodic orbit, an appropriate continuous controlling signal is injected into the system, whose intensity is nearly zero as the system evolves close to the desired periodic orbit but increases when it drifts away from the desired orbit. Both the Pyragas and OGY methods are part of a general class of methods called "closed loop" or "feedback" methods which can be applied based on knowledge of the system obtained through solely observing the behavior of the system as a whole over a suitable period of time. The method was proposed by Lithuanian physicist Kęstutis Pyragas.
References
- 1 2 González-Miranda, J.M. (2004). Synchronization and Control of Chaos: An Introduction for Scientists and Engineers. London: Imperial College Press. Bibcode:2004scci.book.....G.
- ↑ Eckehard Schöll and Heinz Georg Schuster (2007). Handbook of Chaos Control. Weinheim: Wiley-VCH.
- ↑ Fradkov A.L. and Pogromsky A.Yu. (1998). Introduction to Control of Oscillations and Chaos. Singapore: World Scientific Publishers.
- ↑ Ditto, William; Louis M. Pecora (August 1993). "Mastering Chaos". Scientific American.
- ↑ S. Boccaletti et al.(2000) The Control of Chaos: Theory and Applications, Physics Reports 329, 103-197 Archived 2016-03-04 at the Wayback Machine .
- ↑ Sarnobat, S.U. (August 2000). "Modification, Identification & Control of Chaotic Bubbling via Electrostatic Potential". University of Tennessee. Masters Thesis.

