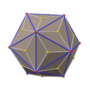
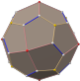
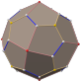
In geometry, an Archimedean solid is one of 13 convex polyhedra whose faces are regular polygons and whose vertices are all symmetric to each other. They were first enumerated by Archimedes. They belong to the class of convex uniform polyhedra, the convex polyhedra with regular faces and symmetric vertices, which is divided into the Archimedean solids, the five Platonic solids, and the two infinite families of prisms and antiprisms. The pseudorhombicuboctahedron is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. An even larger class than the convex uniform polyhedra is the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices.

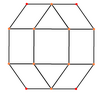
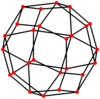
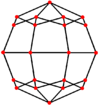
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.
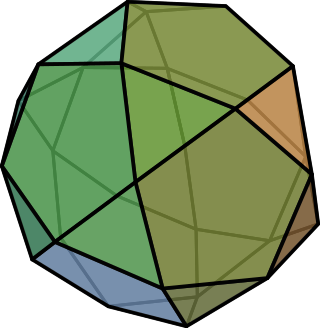
In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid with 38 faces: 6 squares and 32 equilateral triangles. It has 60 edges and 24 vertices.
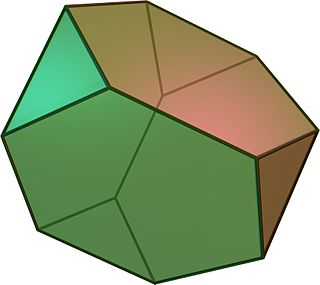
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron at one third of the original edge length.

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.

In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.

In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.

In geometry, a disdyakis dodecahedron,, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it.

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.

In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.

In geometry, the Waterman polyhedra are a family of polyhedra discovered around 1990 by the mathematician Steve Waterman. A Waterman polyhedron is created by packing spheres according to the cubic close(st) packing (CCP), also known as the face-centered cubic (fcc) packing, then sweeping away the spheres that are farther from the center than a defined radius, then creating the convex hull of the sphere centers.
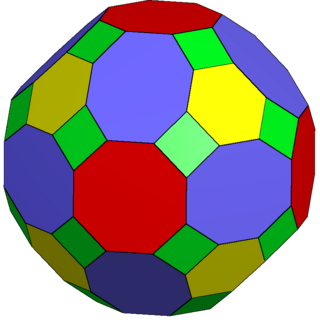
The truncated rhombicuboctahedron is a polyhedron, constructed as a truncation of the rhombicuboctahedron. It has 50 faces consisting of 18 octagons, 8 hexagons, and 24 squares. It can fill space with the truncated cube, truncated tetrahedron and triangular prism as a truncated runcic cubic honeycomb.
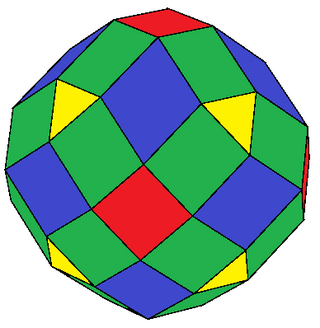
The expanded cuboctahedron is a polyhedron constructed by expansion of the cuboctahedron. It has 50 faces: 8 triangles, 30 squares, and 12 rhombs. The 48 vertices exist at two sets of 24, with a slightly different distance from its center.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.