
In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,
In mathematics, a series is, roughly speaking, the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as

A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables s with Re(s) > 1 and a ≠ 0, −1, −2, … by

In mathematics, the polylogarithm (also known as Jonquière's function, for Alfred Jonquière) is a special function Lis(z) of order s and argument z. Only for special values of s does the polylogarithm reduce to an elementary function such as the natural logarithm or a rational function. In quantum statistics, the polylogarithm function appears as the closed form of integrals of the Fermi–Dirac distribution and the Bose–Einstein distribution, and is also known as the Fermi–Dirac integral or the Bose–Einstein integral. In quantum electrodynamics, polylogarithms of positive integer order arise in the calculation of processes represented by higher-order Feynman diagrams.
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up more than a century later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
In mathematics, the question of whether the Fourier series of a periodic function converges to a given function is researched by a field known as classical harmonic analysis, a branch of pure mathematics. Convergence is not necessarily given in the general case, and certain criteria must be met for convergence to occur.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:
In mathematics, the Leibniz formula for π, named after Gottfried Wilhelm Leibniz, states that
In mathematics, the Lerch zeta function, sometimes called the Hurwitz–Lerch zeta function, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after Czech mathematician Mathias Lerch, who published a paper about the function in 1887.
In mathematics, the Dirichlet–Jordan test gives sufficient conditions for a real-valued, periodic function f to be equal to the sum of its Fourier series at a point of continuity. Moreover, the behavior of the Fourier series at points of discontinuity is determined as well. It is one of many conditions for the convergence of Fourier series.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.

In mathematics, the Dirichlet beta function is a special function, closely related to the Riemann zeta function. It is a particular Dirichlet L-function, the L-function for the alternating character of period four.
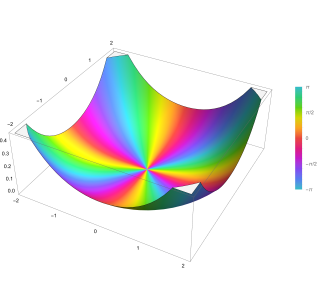
In applied mathematics, the Kelvin functions berν(x) and beiν(x) are the real and imaginary parts, respectively, of
In probability theory and directional statistics, a wrapped probability distribution is a continuous probability distribution that describes data points that lie on a unit n-sphere. In one dimension, a wrapped distribution consists of points on the unit circle. If is a random variate in the interval with probability density function (PDF) , then is a circular variable distributed according to the wrapped distribution and is an angular variable in the interval distributed according to the wrapped distribution .

In mathematical analysis, the Dirichlet kernel, named after the German mathematician Peter Gustav Lejeune Dirichlet, is the collection of periodic functions defined as
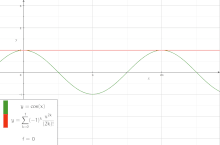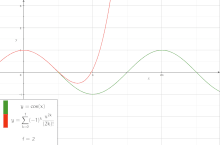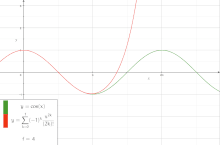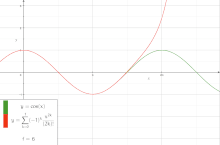






![Convergence and divergence of partial sums of the Dirichlet series defining the Riemann zeta function. Here, the yellow line represents the first fifty successive partial sums
[?]
n
=
1
k
n
-
s
,
{\textstyle \sum _{n=1}^{k}n^{-s},}
the magenta dotted line represents
n
-
s
+
1
-
s
+
1
+
z
(
s
)
,
{\displaystyle {\tfrac {n^{-s+1}}{-s+1}}+\zeta (s),}
and the green dot represents
z
(
s
)
{\displaystyle \zeta (s)}
as s is varied from -0.5 to 1.5. ZetaSpiral.gif](http://upload.wikimedia.org/wikipedia/commons/thumb/a/af/ZetaSpiral.gif/220px-ZetaSpiral.gif)
























