A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.

In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.

In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere, onto a plane perpendicular to the diameter through the point. It is a smooth, bijective function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angles at which curves meet and thus locally approximately preserves shapes. It is neither isometric nor equiareal.

Spherical geometry or spherics is the geometry of the two-dimensional surface of a sphere or the n-dimensional surface of higher dimensional spheres.
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

In four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.
In geometry, inversive geometry is the study of inversion, a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry become much more tractable when an inversion is applied. Inversion seems to have been discovered by a number of people contemporaneously, including Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs and Ingram (1842–3) and Kelvin (1845).

In mathematics, two points of a sphere are called antipodal or diametrically opposite if they are the endpoints of a diameter, a straight line segment between two points on a sphere and passing through its center.

The great-circle distance, orthodromic distance, or spherical distance is the distance along a great circle.

In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane, denoted below as H, together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry.

A gnomonic projection, also known as a central projection or rectilinear projection, is a perspective projection of a sphere, with center of projection at the sphere's center, onto any plane not passing through the center, most commonly a tangent plane. Under gnomonic projection every great circle on the sphere is projected to a straight line in the plane. More generally, a gnomonic projection can be taken of any n-dimensional hypersphere onto a hyperplane.

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.

In hyperbolic geometry, a horocycle, sometimes called an oricycle or limit circle, is a curve of constant curvature which converges asymptotically in both directions to a single ideal point, called the centre of the horocycle. The perpendicular geodesics through every point on a horocycle are limiting parallels, and also all converge asymptotically to the centre. It is the two-dimensional case of a horosphere.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
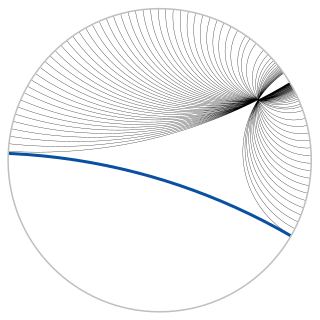
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.

In mathematics, a spherical conic or sphero-conic is a curve on the sphere, the intersection of the sphere with a concentric elliptic cone. It is the spherical analog of a conic section in the plane, and as in the planar case, a spherical conic can be defined as the locus of points the sum or difference of whose great-circle distances to two foci is constant. By taking the antipodal point to one focus, every spherical ellipse is also a spherical hyperbola, and vice versa. As a space curve, a spherical conic is a quartic, though its orthogonal projections in three principal axes are planar conics. Like planar conics, spherical conics also satisfy a "reflection property": the great-circle arcs from the two foci to any point on the conic have the tangent and normal to the conic at that point as their angle bisectors.
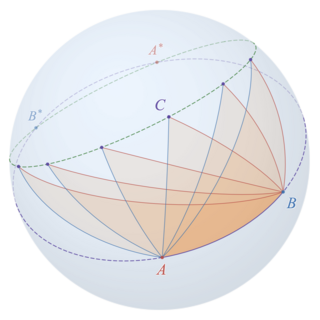
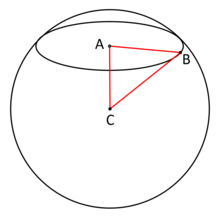
In spherical geometry, Lexell's theorem holds that every spherical triangle with the same surface area on a fixed base has its apex on a small circle, called Lexell's circle or Lexell's locus, passing through each of the two points antipodal to the two base vertices.