In complex analysis, a branch of mathematics, the Casorati–Weierstrass theorem describes the behaviour of holomorphic functions near their essential singularities. It is named for Karl Theodor Wilhelm Weierstrass and Felice Casorati. In Russian literature it is called Sokhotski's theorem.
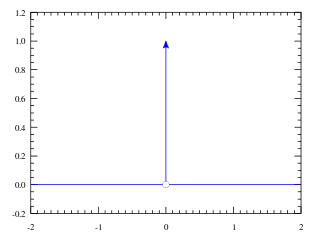
In mathematical analysis, the Dirac delta function, also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limits or, as is common in mathematics, measure theory and the theory of distributions.
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input which may or may not be in the domain of the function.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In mathematics, the symmetry of second derivatives refers to the possibility of interchanging the order of taking partial derivatives of a function
In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.

In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. Propagators may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.

In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:

In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter θ0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to θ0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to θ0 converges to one.

Arc length is the distance between two points along a section of a curve.

The small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians:
In calculus, the Leibniz integral rule for differentiation under the integral sign states that for an integral of the form
In mathematics, more specifically in dynamical systems, the method of averaging exploits systems containing time-scales separation: a fast oscillationversus a slow drift. It suggests that we perform an averaging over a given amount of time in order to iron out the fast oscillations and observe the qualitative behavior from the resulting dynamics. The approximated solution holds under finite time inversely proportional to the parameter denoting the slow time scale. It turns out to be a customary problem where there exists the trade off between how good is the approximated solution balanced by how much time it holds to be close to the original solution.
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by Hermann Weyl. There is a closely related formula for the character of an irreducible representation of a semisimple Lie algebra. In Weyl's approach to the representation theory of connected compact Lie groups, the proof of the character formula is a key step in proving that every dominant integral element actually arises as the highest weight of some irreducible representation. Important consequences of the character formula are the Weyl dimension formula and the Kostant multiplicity formula.

The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable. For example, the derivative of the sine function is written sin′(a) = cos(a), meaning that the rate of change of sin(x) at a particular angle x = a is given by the cosine of that angle.

Anatoly Alexeyevich Karatsuba was a Russian mathematician working in the field of analytic number theory, p-adic numbers and Dirichlet series.
The narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology.
In mathematics, singular integral operators of convolution type are the singular integral operators that arise on Rn and Tn through convolution by distributions; equivalently they are the singular integral operators that commute with translations. The classical examples in harmonic analysis are the harmonic conjugation operator on the circle, the Hilbert transform on the circle and the real line, the Beurling transform in the complex plane and the Riesz transforms in Euclidean space. The continuity of these operators on L2 is evident because the Fourier transform converts them into multiplication operators. Continuity on Lp spaces was first established by Marcel Riesz. The classical techniques include the use of Poisson integrals, interpolation theory and the Hardy–Littlewood maximal function. For more general operators, fundamental new techniques, introduced by Alberto Calderón and Antoni Zygmund in 1952, were developed by a number of authors to give general criteria for continuity on Lp spaces. This article explains the theory for the classical operators and sketches the subsequent general theory.




















![x
2
sin
[?]
(
1
x
)
{\displaystyle x^{2}\sin \left({\tfrac {1}{x}}\right)}
being squeezed in the limit as x goes to 0 Inst satsen.png](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e4/Inst_satsen.png/250px-Inst_satsen.png)







![Comparing areas:
A
(
^
A
D
B
)
<=
A
(
sector
A
D
B
)
<=
A
(
^
A
D
F
)
=
1
2
[?]
sin
[?]
x
[?]
1
<=
x
2
p
[?]
p
<=
1
2
[?]
tan
[?]
x
[?]
1
=
sin
[?]
x
<=
x
<=
sin
[?]
x
cos
[?]
x
=
cos
[?]
x
sin
[?]
x
<=
1
x
<=
1
sin
[?]
x
=
cos
[?]
x
<=
sin
[?]
x
x
<=
1
{\displaystyle {\begin{array}{cccccc}&A(\triangle ADB)&\leq &A({\text{sector }}ADB)&\leq &A(\triangle ADF)\\[4pt]\Rightarrow &{\frac {1}{2}}\cdot \sin x\cdot 1&\leq &{\frac {x}{2\pi }}\cdot \pi &\leq &{\frac {1}{2}}\cdot \tan x\cdot 1\\[4pt]\Rightarrow &\sin x&\leq &x&\leq &{\frac {\sin x}{\cos x}}\\[4pt]\Rightarrow &{\frac {\cos x}{\sin x}}&\leq &{\frac {1}{x}}&\leq &{\frac {1}{\sin x}}\\[4pt]\Rightarrow &\cos x&\leq &{\frac {\sin x}{x}}&\leq &1\end{array}}} Limit sin x x.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/1/10/Limit_sin_x_x.svg/330px-Limit_sin_x_x.svg.png)
























