
The number e is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of natural logarithms. It is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the computation of compound interest. It can also be calculated as the sum of the infinite series

In probability theory, the expected value is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would "expect" to get in reality.

In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of successes occurs. For example, we can define rolling a 6 on a dice as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success. In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution.
In economics, utility is a measure of the satisfaction that a certain person has from a certain state of the world. Over time, the term has been used in two different meanings.
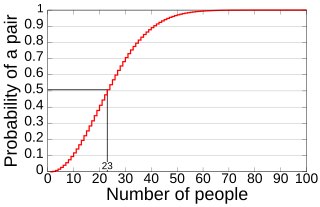
In probability theory, the birthday problem asks for the probability that, in a set of n randomly chosen people, at least two will share a birthday. The birthday paradox refers to the counterintuitive fact that only 23 people are needed for that probability to exceed 50%.

In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variablesXi are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin. Every variable Xi in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes ; this generalization is known as the Bernoulli scheme.
In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions:

In probability theory, the law of large numbers (LLN) is a mathematical theorem that states that the average of the results obtained from a large number of independent and identical random samples converges to the true value, if it exists. More formally, the LLN states that given a sample of independent and identically distributed values, the sample mean converges to the true mean.

In economics and finance, risk aversion is the tendency of people to prefer outcomes with low uncertainty to those outcomes with high uncertainty, even if the average outcome of the latter is equal to or higher in monetary value than the more certain outcome.

In statistics, the logistic model is a statistical model that models the log-odds of an event as a linear combination of one or more independent variables. In regression analysis, logistic regression is estimating the parameters of a logistic model. Formally, in binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable or a continuous variable. The corresponding probability of the value labeled "1" can vary between 0 and 1, hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. See § Background and § Definition for formal mathematics, and § Example for a worked example.
A martingale is a class of betting strategies that originated from and were popular in 18th-century France. The simplest of these strategies was designed for a game in which the gambler wins the stake if a coin comes up heads and loses if it comes up tails. The strategy had the gambler double the bet after every loss, so that the first win would recover all previous losses plus win a profit equal to the original stake. Thus the strategy is an instantiation of the St. Petersburg paradox.
The expected utility hypothesis is a foundational assumption in mathematical economics concerning decision making under uncertainty. It postulates that rational agents maximize utility, meaning the subjective desirability of their actions. Rational choice theory, a cornerstone of microeconomics, builds this postulate to model aggregate social behaviour.

The two envelopes problem, also known as the exchange paradox, is a paradox in probability theory. It is of special interest in decision theory and for the Bayesian interpretation of probability theory. It is a variant of an older problem known as the necktie paradox. The problem is typically introduced by formulating a hypothetical challenge like the following example:
Imagine you are given two identical envelopes, each containing money. One contains twice as much as the other. You may pick one envelope and keep the money it contains. Having chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?

In probability theory, the Kelly criterion is a formula for sizing a bet. The Kelly bet size is found by maximizing the expected value of the logarithm of wealth, which is equivalent to maximizing the expected geometric growth rate. Assuming that the expected returns are known, the Kelly criterion leads to higher wealth than any other strategy in the long run. J. L. Kelly Jr, a researcher at Bell Labs, described the criterion in 1956.
The Allais paradox is a choice problem designed by Maurice Allais to show an inconsistency of actual observed choices with the predictions of expected utility theory. Rather than adhering to rationality, the Allais paradox proves that individuals rarely make rational decisions consistently when required to do so immediately. The independence axiom of expected utility theory, which requires that the preferences of an individual should not change when altering two lotteries by equal proportions, was proven to be violated by the paradox.
In probability theory, the Chinese restaurant process is a discrete-time stochastic process, analogous to seating customers at tables in a restaurant. Imagine a restaurant with an infinite number of circular tables, each with infinite capacity. Customer 1 sits at the first table. The next customer either sits at the same table as customer 1, or the next table. This continues, with each customer choosing to either sit at an occupied table with a probability proportional to the number of customers already there, or an unoccupied table. At time n, the n customers have been partitioned among m ≤ n tables. The results of this process are exchangeable, meaning the order in which the customers sit does not affect the probability of the final distribution. This property greatly simplifies a number of problems in population genetics, linguistic analysis, and image recognition.

In information theory, the binary entropy function, denoted or , is defined as the entropy of a Bernoulli process with probability of one of two values. It is a special case of , the entropy function. Mathematically, the Bernoulli trial is modelled as a random variable that can take on only two values: 0 and 1, which are mutually exclusive and exhaustive.
The mathematics of gambling is a collection of probability applications encountered in games of chance and can get included in game theory. From a mathematical point of view, the games of chance are experiments generating various types of aleatory events, and it is possible to calculate by using the properties of probability on a finite space of possibilities.
In probability theory, the de Moivre–Laplace theorem, which is a special case of the central limit theorem, states that the normal distribution may be used as an approximation to the binomial distribution under certain conditions. In particular, the theorem shows that the probability mass function of the random number of "successes" observed in a series of independent Bernoulli trials, each having probability of success, converges to the probability density function of the normal distribution with mean and standard deviation , as grows large, assuming is not or .
In decision theory, the von Neumann–Morgenstern (VNM) utility theorem shows that, under certain axioms of rational behavior, a decision-maker faced with risky (probabilistic) outcomes of different choices will behave as if they are maximizing the expected value of some function defined over the potential outcomes at some specified point in the future. This function is known as the von Neumann–Morgenstern utility function. The theorem is the basis for expected utility theory.



















