Structural cut-off

Last updated February 25, 2019

The structural cut-off is a concept in network science which imposes a degree cut-off in the degree distribution of a finite size network due to structural limitations (such as the simple graph property). Networks with vertices with degree higher than the structural cut-off will display structural disassortativity.

Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by nodes and the connections between the elements or actors as links. The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena."

In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.

Assortativity, or assortative mixing is a preference for a network's nodes to attach to others that are similar in some way. Though the specific measure of similarity may vary, network theorists often examine assortativity in terms of a node's degree. The addition of this characteristic to network models more closely approximates the behaviors of many real world networks.

Definition

The structural cut-off is a maximum degree cut-off that arises from the structure of a finite size network.

Let $E_{kk'}$ be the number of edges between all vertices of degree $k$ and $k'$ if $k\neq k'$ , and twice the number if $k=k'$ . Given that multiple edges between two vertices are not allowed, $E_{kk'}$ is bounded by the maximum number of edges between two degree classes $m_{kk'}$ .

Then, the ratio can be written

r_{kk'}\equiv {\frac {E_{kk'}}{m_{kk'}}}={\frac {\langle k\rangle P(k,k')}{\min\{kP(k),k'P(k'),NP(k)P(k')\}}}

,

where $\langle k\rangle$ is the average degree of the network, $N$ is the total number of vertices, $P(k)$ is the probability a randomly chosen vertex will have degree $k$ , and $P(k,k')=E_{kk'}/\langle k\rangle N$ is the probability that a randomly picked edge will connect on one side a vertex with degree $k$ with a vertex of degree $k'$ .

To be in the physical region, $r_{kk'}\leq 1$ must be satisfied.

The structural cut-off $k_{s}$ is then defined by $r_{k_{s}k_{s}}=1$ . ^[1]

Structural cut-off for neutral networks

The structural cut-off plays an important role in neutral (or uncorrelated) networks, which do not display any assortativity. The cut-off takes the form

k_{s}\sim (\langle k\rangle N)^{1/2}

which is finite in any real network.

Thus, if vertices of degree $k\geq k_{s}$ exist, it is physically impossible to attach enough edges between them to maintain the neutrality of the network.

Structural disassortativity in scale-free networks

In a scale-free network the degree distribution is described by a power law with characteristic exponent $\gamma$ , $P(k)\sim k^{-\gamma }$ . In a finite scale free network, the maximum degree of any vertex (also called the natural cut-off), scales as

A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as

k_{\text{max}}\sim N^{\frac {1}{\gamma -1}}

.

Then, networks with $\gamma <3$ , which is the regime of most real networks, will have $k_{\text{max}}$ diverging faster than $k_{s}\sim N^{1/2}$ in a neutral network. This has the important implication that an otherwise neutral network may show disassortative degree correlations if $k_{\text{max}}>k_{s}$ . This disassortativity is not a result of any microscopic property of the network, but is purely due to the structural limitations of the network. In the analysis of networks, for a degree correlation to be meaningful, it must be checked that the correlations are not of structural origin.

Impact of the structural cut-off

Generated networks

A network generated randomly by a network generation algorithm is in general not free of structural disassortativity. If a neutral network is required, then structural disassortativity must be avoided. There are a few methods by which this can be done: ^[2]

Allow multiple edges between the same two vertices. While this means that the network is no longer a simple network, it allows for sufficient edges to maintain neutrality.
Simply remove all vertices with degree $k>k_{s}$ . This guarantees that no vertex is subject to structural limitations in its edges, and the network is free of structural disassortativity.

Real networks

In some real networks, the same methods as for generated networks can also be used. In many cases, however, it may not make sense to consider multiple edges between two vertices, or such information is not available. The high degree vertices (hubs) may also be an important part of the network that cannot be removed without changing other fundamental properties.

To determine whether the assortativity or disassortativity of a network is of structural origin, the network can be compared with a degree-preserving randomized version of itself (without multiple edges). Then any assortativity measure of the randomized version will be a result of the structural cut-off. If the real network displays any additional assortativity or disassortativity beyond the structural disassortativity, then it is a meaningful property of the real network.

Other quantities that depend on the degree correlations, such as some definitions of the rich-club coefficient, will also be impacted by the structural cut-off. ^[3]

The rich-club coefficient is a metric on graphs and networks, designed to measure the extent to which well-connected nodes also connect to each other. Networks which have a relatively high rich-club coefficient are said to demonstrate the rich-club effect and will have many connections between nodes of high degree. This effect has been measured and noted on scientific collaboration networks and air transportation networks. It has been shown to be significantly lacking on protein interaction networks.

Related Research Articles

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation V of a quiver assigns a vector space V(x) to each vertex x of the quiver and a linear map V(a) to each arrow a.

In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group. It is a central tool in combinatorial and geometric group theory.

In mathematics, random graph is the general term to refer to probability distributions over graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of typical graphs. Its practical applications are found in all areas in which complex networks need to be modeled – a large number of random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, random graph refers almost exclusively to the Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a random graph.

In mathematics, loop-erased random walk is a model for a random simple path with important applications in combinatorics and, in physics, quantum field theory. It is intimately connected to the uniform spanning tree, a model for a random tree. See also random walk for more general treatment of this topic.

In mathematics, an Artin group is a group with a presentation of the form

In the mathematical field of graph theory, the Laplacian matrix, sometimes called admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation of a graph. The Laplacian matrix can be used to find many useful properties of a graph. Together with Kirchhoff's theorem, it can be used to calculate the number of spanning trees for a given graph. The sparsest cut of a graph can be approximated through the second smallest eigenvalue of its Laplacian by Cheeger's inequality. It can also be used to construct low dimensional embeddings, which can be useful for a variety of machine learning applications.

In network theory, a giant component is a connected component of a given random graph that contains a finite fraction of the entire graph's vertices.

In mathematics, the Cameron–Martin theorem or Cameron–Martin formula is a theorem of measure theory that describes how abstract Wiener measure changes under translation by certain elements of the Cameron–Martin Hilbert space.

Mixing patterns refer to systematic tendencies of one type of nodes in a network to connect to another type. For instance, nodes might tend to link to others that are very similar or very different. This feature is common in many social networks, although it also appears sometimes in non-social networks. Mixing patterns are closely related to assortativity; however, for the purposes of this article, the term is used to refer to assortative or disassortative mixing based on real-world factors, either topological or sociological.

In the mathematical field of graph theory, the Erdős–Rényi model is either of two closely related models for generating random graphs. They are named after mathematicians Paul Erdős and Alfréd Rényi, who first introduced one of the models in 1959, while Edgar Gilbert introduced the other model contemporaneously and independently of Erdős and Rényi. In the model of Erdős and Rényi, all graphs on a fixed vertex set with a fixed number of edges are equally likely; in the model introduced by Gilbert, each edge has a fixed probability of being present or absent, independently of the other edges. These models can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs.

In mathematics, the Fortuin–Kasteleyn–Ginibre (FKG) inequality is a correlation inequality, a fundamental tool in statistical mechanics and probabilistic combinatorics, due to Cees M. Fortuin, Pieter W. Kasteleyn, and Jean Ginibre (1971). Informally, it says that in many random systems, increasing events are positively correlated, while an increasing and a decreasing event are negatively correlated.

In mathematics, a packing in a hypergraph is a partition of the set of the hypergraph's edges into a number of disjoint subsets such that no pair of edges in each subset share any vertex. There are two famous algorithms to achieve asymptotically optimal packing in k-uniform hypergraphs. One of them is a random greedy algorithm which was proposed by Joel Spencer. He used a branching process to formally prove the optimal achievable bound under some side conditions. The other algorithm is called the Rödl nibble and was proposed by Vojtěch Rödl et al. They showed that the achievable packing by the Rödl nibble is in some sense close to that of the random greedy algorithm.

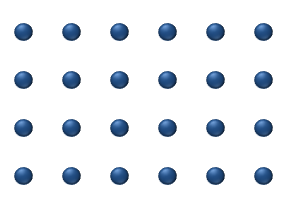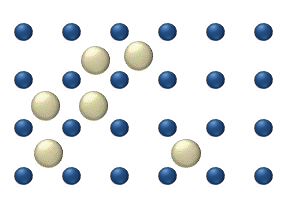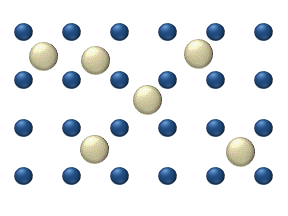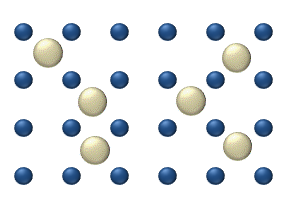
In statistical mechanics, thermal fluctuations are random deviations of a system from its average state, that occur in a system at equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they decrease as temperature approaches absolute zero.

In mathematics, specifically group theory, a descendant tree is a hierarchical structure for visualizing parent-descendant relations between isomorphism classes of finite groups of prime power order $, for a fixed prime number and varying integer exponents . Such groups are briefly called finite p-groups . The vertices of a descendant tree are isomorphism classes of finite p -groups.$

A hyperbolic geometric graph (HGG) or hyperbolic geometric network (HGN) is a special type of spatial network where (1) latent coordinates of nodes are sprinkled according to a probability density function into a hyperbolic space of constant negative curvature and (2) an edge between two nodes is present if they are close according to a function of the metric. A HGG generalizes a random geometric graph (RGG) whose embedding space is Euclidean.

Lancichinetti–Fortunato–Radicchi (LFR)benchmark is an algorithm that generates benchmark networks. They have a priori known communities and are used to compare different community detection methods. The advantage of LFR over other methods is that it accounts for the heterogeneity in the distributions of node degrees and of community sizes.

In network science, the configuration model is a method for generating random networks from given degree sequence. It is widely used as a reference model for real-life social networks, because it allows the user to incorporate arbitrary degree distributions.

References

↑ Boguna, M.; Pastor-Satorras, R.; Vespignani, A. (1 March 2004). "Cut-offs and finite size effects in scale-free networks". The European Physical Journal B. 38 (2): 205–209. arXiv: cond-mat/0311650  . Bibcode:2004EPJB...38..205B. doi:10.1140/epjb/e2004-00038-8.
↑ Catanzaro, Michele; Boguñá, Marián; Pastor-Satorras, Romualdo (February 2005). "Generation of uncorrelated random scale-free networks". Physical Review E. 71 (2). arXiv: cond-mat/0408110  . Bibcode:2005PhRvE..71b7103C. doi:10.1103/PhysRevE.71.027103.
↑ Zhou, S; Mondragón, R J (28 June 2007). "Structural constraints in complex networks". New Journal of Physics. 9 (6): 173–173. arXiv: physics/0702096  . Bibcode:2007NJPh....9..173Z. doi:10.1088/1367-2630/9/6/173.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Boguna, M.; Pastor-Satorras, R.; Vespignani, A. (1 March 2004). "Cut-offs and finite size effects in scale-free networks". The European Physical Journal B. 38 (2): 205–209. arXiv: cond-mat/0311650  . Bibcode:2004EPJB...38..205B. doi:10.1140/epjb/e2004-00038-8.

[2] Catanzaro, Michele; Boguñá, Marián; Pastor-Satorras, Romualdo (February 2005). "Generation of uncorrelated random scale-free networks". Physical Review E. 71 (2). arXiv: cond-mat/0408110  . Bibcode:2005PhRvE..71b7103C. doi:10.1103/PhysRevE.71.027103.

[3] Zhou, S; Mondragón, R J (28 June 2007). "Structural constraints in complex networks". New Journal of Physics. 9 (6): 173–173. arXiv: physics/0702096  . Bibcode:2007NJPh....9..173Z. doi:10.1088/1367-2630/9/6/173.