A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable—that is, a matrix in which some or all elements are random variables. Many important properties of physical systems can be represented mathematically as matrix problems. For example, the thermal conductivity of a lattice can be computed from the dynamical matrix of the particle-particle interactions within the lattice.

In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.
The Kuramoto model, first proposed by Yoshiki Kuramoto, is a mathematical model used in describing synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators. Its formulation was motivated by the behavior of systems of chemical and biological oscillators, and it has found widespread applications in areas such as neuroscience and oscillating flame dynamics. Kuramoto was quite surprised when the behavior of some physical systems, namely coupled arrays of Josephson junctions, followed his model.

The Barabási–Albert (BA) model is an algorithm for generating random scale-free networks using a preferential attachment mechanism. Several natural and human-made systems, including the Internet, the World Wide Web, citation networks, and some social networks are thought to be approximately scale-free and certainly contain few nodes with unusually high degree as compared to the other nodes of the network. The BA model tries to explain the existence of such nodes in real networks. The algorithm is named for its inventors Albert-László Barabási and Réka Albert.

Assortativity, or assortative mixing, is a preference for a network's nodes to attach to others that are similar in some way. Though the specific measure of similarity may vary, network theorists often examine assortativity in terms of a node's degree. The addition of this characteristic to network models more closely approximates the behaviors of many real world networks.
In network science, a gradient network is a directed subnetwork of an undirected "substrate" network where each node has an associated scalar potential and one out-link that points to the node with the smallest potential in its neighborhood, defined as the union of itself and its neighbors on the substrate network.

Fractal analysis is useful in the study of complex networks, present in both natural and artificial systems such as computer systems, brain and social networks, allowing further development of the field in network science.
In theoretical physics, quantum nonlocality refers to the phenomenon by which the measurement statistics of a multipartite quantum system do not allow an interpretation with local realism. Quantum nonlocality has been experimentally verified under a variety of physical assumptions. Any physical theory that aims at superseding or replacing quantum theory should account for such experiments and therefore cannot fulfill local realism; quantum nonlocality is a property of the universe that is independent of our description of nature.
In quantum mechanics, a weak value is a quantity related to a shift of a measuring device's pointer when usually there is pre- and postselection. It should not be confused with a weak measurement, which is often defined in conjunction. The weak value was first defined by Yakir Aharonov, David Albert, and Lev Vaidman, published in Physical Review Letters 1988, and is related to the two-state vector formalism. There is also a way to obtain weak values without postselection.

Quantum complex networks are complex networks whose nodes are quantum computing devices. Quantum mechanics has been used to create secure quantum communications channels that are protected from hacking. Quantum communications offer the potential for secure enterprise-scale solutions.
Robustness, the ability to withstand failures and perturbations, is a critical attribute of many complex systems including complex networks.
In quantum mechanics, weak measurements are a type of quantum measurement that results in an observer obtaining very little information about the system on average, but also disturbs the state very little. From Busch's theorem the system is necessarily disturbed by the measurement. In the literature weak measurements are also known as unsharp, fuzzy, dull, noisy, approximate, and gentle measurements. Additionally weak measurements are often confused with the distinct but related concept of the weak value.
Supersymmetric theory of stochastic dynamics or stochastics (STS) is an exact theory of stochastic (partial) differential equations (SDEs), the class of mathematical models with the widest applicability covering, in particular, all continuous time dynamical systems, with and without noise. The main utility of the theory from the physical point of view is a rigorous theoretical explanation of the ubiquitous spontaneous long-range dynamical behavior that manifests itself across disciplines via such phenomena as 1/f, flicker, and crackling noises and the power-law statistics, or Zipf's law, of instantonic processes like earthquakes and neuroavalanches. From the mathematical point of view, STS is interesting because it bridges the two major parts of mathematical physics – the dynamical systems theory and topological field theories. Besides these and related disciplines such as algebraic topology and supersymmetric field theories, STS is also connected with the traditional theory of stochastic differential equations and the theory of pseudo-Hermitian operators.

In network science, the configuration model is a method for generating random networks from a given degree sequence. It is widely used as a reference model for real-life social networks, because it allows the modeler to incorporate arbitrary degree distributions.
A set of networks that satisfies given structural characteristics can be treated as a network ensemble. Brought up by Ginestra Bianconi in 2007, the entropy of a network ensemble measures the level of the order or uncertainty of a network ensemble.
The continuous spontaneous localization (CSL) model is a spontaneous collapse model in quantum mechanics, proposed in 1989 by Philip Pearle. and finalized in 1990 Gian Carlo Ghirardi, Philip Pearle and Alberto Rimini.
In statistical mechanics, Lee–Yang theory, sometimes also known as Yang–Lee theory, is a scientific theory which seeks to describe phase transitions in large physical systems in the thermodynamic limit based on the properties of small, finite-size systems. The theory revolves around the complex zeros of partition functions of finite-size systems and how these may reveal the existence of phase transitions in the thermodynamic limit.
In network science, the network entropy is a disorder measure derived from information theory to describe the level of randomness and the amount of information encoded in a graph. It is a relevant metric to quantitatively characterize real complex networks and can also be used to quantify network complexity
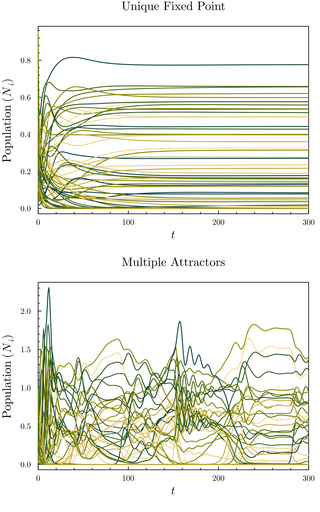
The random generalized Lotka–Volterra model (rGLV) is an ecological model and random set of coupled ordinary differential equations where the parameters of the generalized Lotka–Volterra equation are sampled from a probability distribution, analogously to quenched disorder. The rGLV models dynamics of a community of species in which each species' abundance grows towards a carrying capacity but is depleted due to competition from the presence of other species. It is often analyzed in the many-species limit using tools from statistical physics, in particular from spin glass theory.