
A geometric Brownian motion (GBM) (also known as exponential Brownian motion) is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion (also called a Wiener process) with drift. It is an important example of stochastic processes satisfying a stochastic differential equation (SDE); in particular, it is used in mathematical finance to model stock prices in the Black–Scholes model.
In econometrics, the autoregressive conditional heteroskedasticity (ARCH) model is a statistical model for time series data that describes the variance of the current error term or innovation as a function of the actual sizes of the previous time periods' error terms; often the variance is related to the squares of the previous innovations. The ARCH model is appropriate when the error variance in a time series follows an autoregressive (AR) model; if an autoregressive moving average (ARMA) model is assumed for the error variance, the model is a generalized autoregressive conditional heteroskedasticity (GARCH) model.

A short-rate model, in the context of interest rate derivatives, is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written .
In financial mathematics, the Hull–White model is a model of future interest rates. In its most generic formulation, it belongs to the class of no-arbitrage models that are able to fit today's term structure of interest rates. It is relatively straightforward to translate the mathematical description of the evolution of future interest rates onto a tree or lattice and so interest rate derivatives such as bermudan swaptions can be valued in the model.

In mathematics, the Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. It is named after Leonard Ornstein and George Eugene Uhlenbeck.
The Heath–Jarrow–Morton (HJM) framework is a general framework to model the evolution of interest rate curves – instantaneous forward rate curves in particular. When the volatility and drift of the instantaneous forward rate are assumed to be deterministic, this is known as the Gaussian Heath–Jarrow–Morton (HJM) model of forward rates. For direct modeling of simple forward rates the Brace–Gatarek–Musiela model represents an example.
In mathematical finance, the Black–Derman–Toy model (BDT) is a popular short-rate model used in the pricing of bond options, swaptions and other interest rate derivatives; see Lattice model (finance) § Interest rate derivatives. It is a one-factor model; that is, a single stochastic factor—the short rate—determines the future evolution of all interest rates. It was the first model to combine the mean-reverting behaviour of the short rate with the log-normal distribution, and is still widely used.
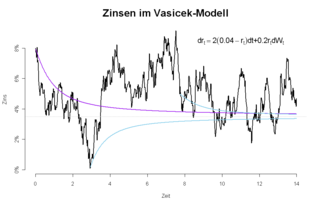
In finance, the Vasicek model is a mathematical model describing the evolution of interest rates. It is a type of one-factor short-rate model as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives, and has also been adapted for credit markets. It was introduced in 1977 by Oldřich Vašíček, and can be also seen as a stochastic investment model.
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others.
In mathematical finance, the SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "stochastic alpha, beta, rho", referring to the parameters of the model. The SABR model is widely used by practitioners in the financial industry, especially in the interest rate derivative markets. It was developed by Patrick S. Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward.
The Rendleman–Bartter model in finance is a short-rate model describing the evolution of interest rates. It is a "one factor model" as it describes interest rate movements as driven by only one source of market risk. It can be used in the valuation of interest rate derivatives. It is a stochastic asset model.

In mathematical finance, the Cox–Ingersoll–Ross (CIR) model describes the evolution of interest rates. It is a type of "one factor model" as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives. It was introduced in 1985 by John C. Cox, Jonathan E. Ingersoll and Stephen A. Ross as an extension of the Vasicek model, itself an Ornstein–Uhlenbeck_process.
In finance, a volatility swap is a forward contract on the future realised volatility of a given underlying asset. Volatility swaps allow investors to trade the volatility of an asset directly, much as they would trade a price index. Its payoff at expiration is equal to
In finance, the Heston model, named after Steven L. Heston, is a mathematical model that describes the evolution of the volatility of an underlying asset. It is a stochastic volatility model: such a model assumes that the volatility of the asset is not constant, nor even deterministic, but follows a random process.
A local volatility model, in mathematical finance and financial engineering, is an option pricing model that treats volatility as a function of both the current asset level and of time . As such, it is a generalisation of the Black–Scholes model, where the volatility is a constant. Local volatility models are often compared with stochastic volatility models, where the instantaneous volatility is not just a function of the asset level but depends also on a new "global" randomness coming from an additional random component.
In financial econometrics, the Markov-switching multifractal (MSM) is a model of asset returns developed by Laurent E. Calvet and Adlai J. Fisher that incorporates stochastic volatility components of heterogeneous durations. MSM captures the outliers, log-memory-like volatility persistence and power variation of financial returns. In currency and equity series, MSM compares favorably with standard volatility models such as GARCH(1,1) and FIGARCH both in- and out-of-sample. MSM is used by practitioners in the financial industry to forecast volatility, compute value-at-risk, and price derivatives.
The Brownian motion models for financial markets are based on the work of Robert C. Merton and Paul A. Samuelson, as extensions to the one-period market models of Harold Markowitz and William F. Sharpe, and are concerned with defining the concepts of financial assets and markets, portfolios, gains and wealth in terms of continuous-time stochastic processes.
In financial mathematics, the Black–Karasinski model is a mathematical model of the term structure of interest rates; see short-rate model. It is a one-factor model as it describes interest rate movements as driven by a single source of randomness. It belongs to the class of no-arbitrage models, i.e. it can fit today's zero-coupon bond prices, and in its most general form, today's prices for a set of caps, floors or European swaptions. The model was introduced by Fischer Black and Piotr Karasinski in 1991.
An affine term structure model is a financial model that relates zero-coupon bond prices to a spot rate model. It is particularly useful for deriving the yield curve – the process of determining spot rate model inputs from observable bond market data. The affine class of term structure models implies the convenient form that log bond prices are linear functions of the spot rate.
In mathematics, the Chan–Karolyi–Longstaff–Sanders process is a stochastic process with applications to finance. In particular it has been used to model the term structure of interest rates. The CKLS process can also be viewed as a generalization of the Ornstein–Uhlenbeck process. It is named after K. C. Chan, G. Andrew Karolyi, Francis A. Longstaff, and Anthony B. Sanders, with their paper published in 1992.







