Wiener sausage

Last updated September 05, 2022

A short, fat Wiener sausage in 2 dimensions WienerSausage.jpg — A short, fat Wiener sausage in 2 dimensions

In the mathematical field of probability, the Wiener sausage is a neighborhood of the trace of a Brownian motion up to a time t, given by taking all points within a fixed distance of Brownian motion. It can be visualized as a sausage of fixed radius whose centerline is Brownian motion. The Wiener sausage was named after Norbert Wiener by M. D.Donsker and S. R. Srinivasa Varadhan ( 1975 ) because of its relation to the Wiener process; the name is also a pun on Vienna sausage, as "Wiener" is German for "Viennese".

The Wiener sausage is one of the simplest non-Markovian functionals of Brownian motion. Its applications include stochastic phenomena including heat conduction. It was first described by FrankSpitzer ( 1964 ), and it was used by MarkKac and Joaquin Mazdak Luttinger ( 1973 , 1974 ) to explain results of a Bose–Einstein condensate, with proofs published by M. D.Donsker and S. R. Srinivasa Varadhan ( 1975 ).

Definitions

The Wiener sausage W_δ(t) of radius δ and length t is the set-valued random variable on Brownian paths b (in some Euclidean space) defined by

W_{\delta }(t)({b})

is the set of points within a distance δ of some point b(x) of the path b with 0≤x≤t.

Volume of the Wiener sausage

There has been a lot of work on the behavior of the volume (Lebesgue measure) |W_δ(t)| of the Wiener sausage as it becomes thin (δ→0); by rescaling, this is essentially equivalent to studying the volume as the sausage becomes long (t→∞).

Spitzer (1964) showed that in 3 dimensions the expected value of the volume of the sausage is

E(|W_{\delta }(t)|)=2\pi \delta t+4\delta ^{2}{\sqrt {2\pi t}}+4\pi \delta ^{3}/3.

In dimension d at least 3 the volume of the Wiener sausage is asymptotic to

\delta ^{d-2}\pi ^{d/2}2t/\Gamma ((d-2)/2)

as t tends to infinity. In dimensions 1 and 2 this formula gets replaced by ${\sqrt {8t/\pi }}$ and $2{\pi }t/\log(t)$ respectively. Whitman (1964), a student of Spitzer, proved similar results for generalizations of Wiener sausages with cross sections given by more general compact sets than balls.

Related Research Articles

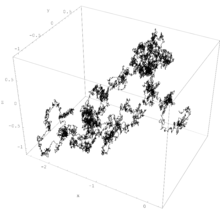
Brownian motion, or pedesis, is the random motion of particles suspended in a medium.

In mathematics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.

In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown. It is one of the best known Lévy processes and occurs frequently in pure and applied mathematics, economics, quantitative finance, evolutionary biology, and physics.

Functional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions. Functional integrals arise in probability, in the study of partial differential equations, and in the path integral approach to the quantum mechanics of particles and fields.

In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random, in which displacements in pairwise disjoint time intervals are independent, and displacements in different time intervals of the same length have identical probability distributions. A Lévy process may thus be viewed as the continuous-time analog of a random walk.

In probability theory, fractional Brownian motion (fBm), also called a fractal Brownian motion, is a generalization of Brownian motion. Unlike classical Brownian motion, the increments of fBm need not be independent. fBm is a continuous-time Gaussian process B_H(t) on [0, T], that starts at zero, has expectation zero for all t in [0, T], and has the following covariance function:

A Brownian bridge is a continuous-time stochastic process B(t) whose probability distribution is the conditional probability distribution of a standard Wiener process W(t) subject to the condition that W(T) = 0, so that the process is pinned to the same value at both t = 0 and t = T. More precisely:

Ornstein–Uhlenbeck process Stochastic process modeling random walk with friction

In mathematics, the Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. It is named after Leonard Ornstein and George Eugene Uhlenbeck.

In the Newman–Penrose (NP) formalism of general relativity, Weyl scalars refer to a set of five complex scalars $which encode the ten independent components of the Weyl tensor of a four-dimensional spacetime.$

In mathematical finance, the Black–Scholes equation is a partial differential equation (PDE) governing the price evolution of a European call or European put under the Black–Scholes model. Broadly speaking, the term may refer to a similar PDE that can be derived for a variety of options, or more generally, derivatives.

Events are often triggered when a stochastic or random process first encounters a threshold. The threshold can be a barrier, boundary or specified state of a system. The amount of time required for a stochastic process, starting from some initial state, to encounter a threshold for the first time is referred to variously as a first hitting time. In statistics, first-hitting-time models are a sub-class of survival models. The first hitting time, also called first passage time, of the barrier set $with respect to an instance of a stochastic process is the time until the stochastic process first enters .$

<span class="mw-page-title-main">Diffusion</span> Movement from high to low concentration

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition.

In mathematics, Montgomery's pair correlation conjecture is a conjecture made by Hugh Montgomery (1973) that the pair correlation between pairs of zeros of the Riemann zeta function is

The Brownian motion models for financial markets are based on the work of Robert C. Merton and Paul A. Samuelson, as extensions to the one-period market models of Harold Markowitz and William F. Sharpe, and are concerned with defining the concepts of financial assets and markets, portfolios, gains and wealth in terms of continuous-time stochastic processes.

In probability theory, the arcsine laws are a collection of results for one-dimensional random walks and Brownian motion. The best known of these is attributed to Paul Lévy (1939).

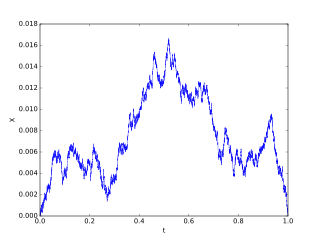
In probability theory a Brownian excursion process is a stochastic process that is closely related to a Wiener process. Realisations of Brownian excursion processes are essentially just realizations of a Wiener process selected to satisfy certain conditions. In particular, a Brownian excursion process is a Wiener process conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive. BEPs are important because, among other reasons, they naturally arise as the limit process of a number of conditional functional central limit theorems.

In theoretical physics, Lovelock's theory of gravity is a generalization of Einstein's theory of general relativity introduced by David Lovelock in 1971. It is the most general metric theory of gravity yielding conserved second order equations of motion in an arbitrary number of spacetime dimensions D. In this sense, Lovelock's theory is the natural generalization of Einstein's General Relativity to higher dimensions. In three and four dimensions, Lovelock's theory coincides with Einstein's theory, but in higher dimensions the theories are different. In fact, for D > 4 Einstein gravity can be thought of as a particular case of Lovelock gravity since the Einstein–Hilbert action is one of several terms that constitute the Lovelock action.

In statistical mechanics, the mean squared displacement is a measure of the deviation of the position of a particle with respect to a reference position over time. It is the most common measure of the spatial extent of random motion, and can be thought of as measuring the portion of the system "explored" by the random walker. In the realm of biophysics and environmental engineering, the Mean Squared Displacement is measured over time to determine if a particle is spreading slowly due to diffusion, or if an advective force is also contributing. Another relevant concept, the Variance-Related Diameter, is also used in studying the transportation and mixing phenomena in the realm of environmental engineering. It prominently appears in the Debye–Waller factor and in the Langevin equation.

The Leimkuhler-Matthews method is an algorithm for finding discretized solutions to the Brownian dynamics

The redundancy principle in biology expresses the need of many copies of the same entity to fulfill a biological function. Examples are numerous: disproportionate numbers of spermatozoa during fertilization compared to one egg, large number of neurotransmitters released during neuronal communication compared to the number of receptors, large numbers of released calcium ions during transient in cells and many more in molecular and cellular transduction or gene activation and cell signaling. This redundancy is particularly relevant when the sites of activation is physically separated from the initial position of the molecular messengers. The redundancy is often generated for the purpose of resolving the time constraint of fast-activating pathways. It can be expressed in terms of the theory of extreme statistics to determine its laws and quantify how shortest paths are selected. The main goal is to estimate these large numbers from physical principles and mathematical derivations.

References

Donsker, M. D.; Varadhan, S. R. S. (1975), "Asymptotics for the Wiener sausage", Communications on Pure and Applied Mathematics, 28 (4): 525–565, doi:10.1002/cpa.3160280406
Hollander, F. den (2001) [1994], "Wiener sausage", Encyclopedia of Mathematics , EMS Press
Kac, M.; Luttinger, J. M. (1973), "Bose-Einstein condensation in the presence of impurities", J. Math. Phys., 14 (11): 1626–1628, Bibcode:1973JMP....14.1626K, doi:10.1063/1.1666234, MR 0342114
Kac, M.; Luttinger, J. M. (1974), "Bose-Einstein condensation in the presence of impurities. II", J. Math. Phys., 15 (2): 183–186, Bibcode:1974JMP....15..183K, doi:10.1063/1.1666617, MR 0342115
Simon, Barry (2005), Functional integration and quantum physics, Providence, RI: AMS Chelsea Publishing, ISBN 0-8218-3582-3, MR 2105995 Especially chapter 22.
Spitzer, F. (1964), "Electrostatic capacity, heat flow and Brownian motion", Probability Theory and Related Fields, 3 (2): 110–121, doi:10.1007/BF00535970, S2CID 198179345
Spitzer, Frank (1976), Principles of random walks, Graduate Texts in Mathematics, vol. 34, New York-Heidelberg: Springer-Verlag, p. 40, MR 0171290 (Reprint of 1964 edition)
Sznitman, Alain-Sol (1998), Brownian motion, obstacles and random media, Springer Monographs in Mathematics, Berlin: Springer-Verlag, doi:10.1007/978-3-662-11281-6, ISBN 3-540-64554-3, MR 1717054 An advanced monograph covering the Wiener sausage.
Whitman, Walter William (1964), Some Strong Laws for Random Walks and Brownian Motion, PhD Thesis, Cornell U.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

v t e Stochastic processes
Discrete time	Bernoulli process Branching process Chinese restaurant process Galton–Watson process Independent and identically distributed random variables Markov chain Moran process Random walk Loop-erased Self-avoiding Biased Maximal entropy
Continuous time	Additive process Bessel process Birth–death process pure birth Brownian motion Bridge Excursion Fractional Geometric Meander Cauchy process Contact process Continuous-time random walk Cox process Diffusion process Empirical process Feller process Fleming–Viot process Gamma process Geometric process Hawkes process Hunt process Interacting particle systems Itô diffusion Itô process Jump diffusion Jump process Lévy process Local time Markov additive process McKean–Vlasov process Ornstein–Uhlenbeck process Poisson process Compound Non-homogeneous Schramm–Loewner evolution Semimartingale Sigma-martingale Stable process Superprocess Telegraph process Variance gamma process Wiener process Wiener sausage
Both	Branching process Galves–Löcherbach model Gaussian process Hidden Markov model (HMM) Markov process Martingale Differences Local Sub- Super- Random dynamical system Regenerative process Renewal process Stochastic chains with memory of variable length White noise
Fields and other	Dirichlet process Gaussian random field Gibbs measure Hopfield model Ising model Potts model Boolean network Markov random field Percolation Pitman–Yor process Point process Cox Poisson Random field Random graph
Time series models	Autoregressive conditional heteroskedasticity (ARCH) model Autoregressive integrated moving average (ARIMA) model Autoregressive (AR) model Autoregressive–moving-average (ARMA) model Generalized autoregressive conditional heteroskedasticity (GARCH) model Moving-average (MA) model
Financial models	Binomial options pricing model Black–Derman–Toy Black–Karasinski Black–Scholes Chan–Karolyi–Longstaff–Sanders (CKLS) Chen Constant elasticity of variance (CEV) Cox–Ingersoll–Ross (CIR) Garman–Kohlhagen Heath–Jarrow–Morton (HJM) Heston Ho–Lee Hull–White LIBOR market Rendleman–Bartter SABR volatility Vašíček Wilkie
Actuarial models	Bühlmann Cramér–Lundberg Risk process Sparre–Anderson
Queueing models	Bulk Fluid Generalized queueing network M/G/1 M/M/1 M/M/c
Properties	Càdlàg paths Continuous Continuous paths Ergodic Exchangeable Feller-continuous Gauss–Markov Markov Mixing Piecewise deterministic Predictable Progressively measurable Self-similar Stationary Time-reversible
Limit theorems	Central limit theorem Donsker's theorem Doob's martingale convergence theorems Ergodic theorem Fisher–Tippett–Gnedenko theorem Large deviation principle Law of large numbers (weak/strong) Law of the iterated logarithm Maximal ergodic theorem Sanov's theorem Zero–one laws (Blumenthal, Borel–Cantelli, Engelbert–Schmidt, Hewitt–Savage, Kolmogorov, Lévy)
Inequalities	Burkholder–Davis–Gundy Doob's martingale Doob's upcrossing Kunita–Watanabe Marcinkiewicz–Zygmund
Tools	Cameron–Martin formula Convergence of random variables Doléans-Dade exponential Doob decomposition theorem Doob–Meyer decomposition theorem Doob's optional stopping theorem Dynkin's formula Feynman–Kac formula Filtration Girsanov theorem Infinitesimal generator Itô integral Itô's lemma Karhunen–Loève theorem Kolmogorov continuity theorem Kolmogorov extension theorem Lévy–Prokhorov metric Malliavin calculus Martingale representation theorem Optional stopping theorem Prokhorov's theorem Quadratic variation Reflection principle Skorokhod integral Skorokhod's representation theorem Skorokhod space Snell envelope Stochastic differential equation Tanaka Stopping time Stratonovich integral Uniform integrability Usual hypotheses Wiener space Classical Abstract
Disciplines	Actuarial mathematics Control theory Econometrics Ergodic theory Extreme value theory (EVT) Large deviations theory Mathematical finance Mathematical statistics Probability theory Queueing theory Renewal theory Ruin theory Signal processing Statistics Stochastic analysis Time series analysis Machine learning
List of topics Category

Wiener sausage

Contents

Definitions

Volume of the Wiener sausage

Related Research Articles

References